Azokat a számpárokat, amelyekre igaz, hogy az egyik szám önmagánál kisebb osztóinak összege megegyezik a másik számmal és fordítva, külön-külön barátságos számoknak, együtt barátságos számpárnak hívjuk.
Másképpen: legyen d(n) az n természetes szám önmagánál kisebb osztóinak összege. Ha d(a)=b és d(b)=a, ahol a≠b, akkor a és b barátságos számpár.
Például: (220; 284), hiszen a 220 önmagánál kisebb osztói: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 és ezek összege 284, illetve 284 önmagánál kisebb osztói: 1, 2, 4, 71, 142 és ezek összege 220.
Írjunk Java programot, amely kiírja az 1-10000 zárt intervallumban található barátságos számpárokat!
1. megoldás
A baratsagosSzamparok1() eljárás ciklusai a brute force módszer szerint behelyesítik az összes lehetséges számot. Minimális lépésszám csökkentésre adódik lehetőség, hiszen a belső ciklus j változója i+1-ről indítható (így a megtalált számpárok nem íródnak ki fordítva is, mert teljesül, hogy i<j).
Az osztokOsszege1(n) függvény is minden lehetséges osztót figyelembe vesz 1-től n-1-ig.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
private static int osztokOsszege1(int n) { int s=0; for(int i=1; i<n; i+=1) if(n%i==0) s+=i; return s; } private static void baratsagosSzamparok1() { System.out.println("Barátságos számpárok 1-től 10000-ig:"); for(int i=1; i<=10000; i++) for(int j=i+1; j<=10000; j++) if(i==osztokOsszege1(j) && j==osztokOsszege1(i)) System.out.println("("+i+"; "+j+")"); } |
2. megoldás
Kisebb módosításokkal a lépésszám csökkenthető. A baratsagosSzamparok2() eljárás külső ciklusánál figyelembe vettem, hogy a legkisebb barátságos számpár kisebb tagja nagyobb 200-nál. Mivel a barátságos számpárok tagjainak paritása mindig megegyezik (azaz mindkettő páros vagy mindkettő páratlan), így a belső ciklus j változója indítható i+2-ről és léptethető kettesével ( j+=2), és továbbra is teljesül, hogy i<j.
Az osztokOsszege2(n) függvényt is módosítottam. Mivel az 1 minden számnak osztója, illetve a 2 minden páros számnak osztója, így s lehet 3 vagy 1 és a ciklus indítható 3-ról. A páros számok esetén a számnál kisebb legnagyobb osztó maximum n/2 lehet, illetve ugyanez páratlan számok esetén n/3 lehet. Ezekre figyelve a max változó adja a ciklus léptetésének felső határát. Az i változó léptetésénél figyelembe vettem, hogy páratlan számnak csak páratlan osztói lehetnek ( i=3-mal szinkronban).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
private static int osztokOsszege2(int n) { int s=(n%2==0?3:1); int max=(n%2==0?n/2:n/3); int lepes=(n%2==0?1:2); for(int i=3; i<=max; i+=lepes) if(n%i==0) s+=i; return s; } private static void baratsagosSzamparok2() { System.out.println("Barátságos számpárok 1-től 10000-ig:"); for(int i=200; i<=10000; i++) for(int j=i+2; j<=10000; j+=2) if(i==osztokOsszege2(j) && j==osztokOsszege2(i)) System.out.println("("+i+"; "+j+")"); } |
3. megoldás
Az eddigi két egymásba ágyazott ciklus helyett átszervezhető a baratsagosSzamparok3() eljárás. A j>i && osztokOsszege2(j)==i feltétel kiértékelése így sokkal hatékonyabb.
|
1 2 3 4 5 6 7 8 |
private static void baratsagosSzamparok3() { System.out.println("Barátságos számpárok 1-től 10000-ig:"); for(int i=200; i<=10000; i++) { int j=osztokOsszege2(i); if(j>i && osztokOsszege2(j)==i) System.out.println("("+i+"; "+j+")"); } } |
Vajon milyen nagyságrendű különbségek adódnak, ha összehasonlítjuk a három megoldás futási idejét?
Mindhárom megoldás helyes és megkapjuk az intervallumban található öt barátságos számpárt: (220; 284), (1184; 1210), (2620; 2924), (5020; 5564), (6232; 6368).
A bejegyzéshez tartozó teljes – időméréssel kiegészített – forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
Források:
- Wikipédia – Barátságos számok
- Wikipedia – Amicable numbers
- www.mathe.tu-freiberg.de – Vollkommene, befreundete und gesellige Zahlen
- gorbem.hu – Barátságok számok
- Hasonló feladat: https://projecteuler.net/problem=21 és megoldás: http://code.jasonbhill.com/c/project-euler-problem-21/
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió alkalomhoz kötődik.
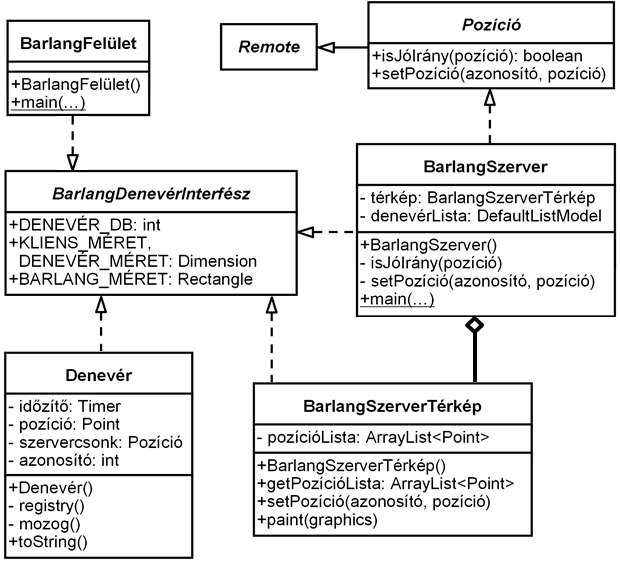
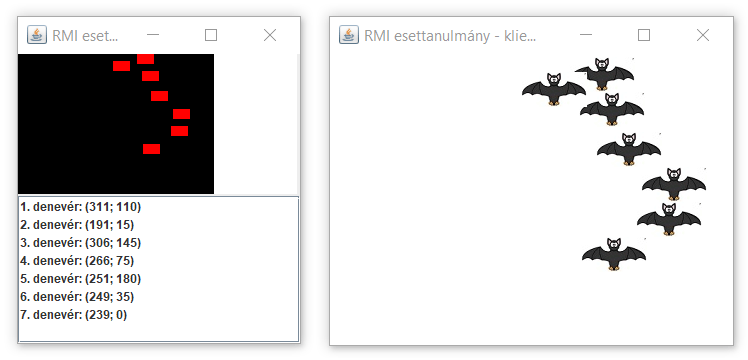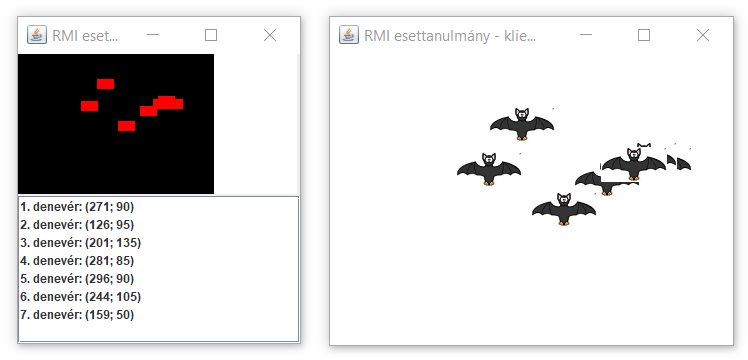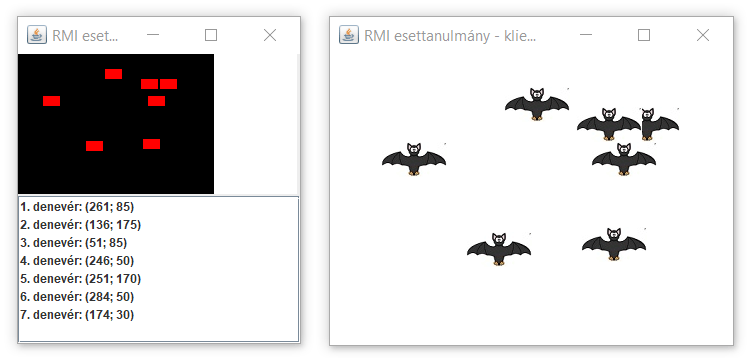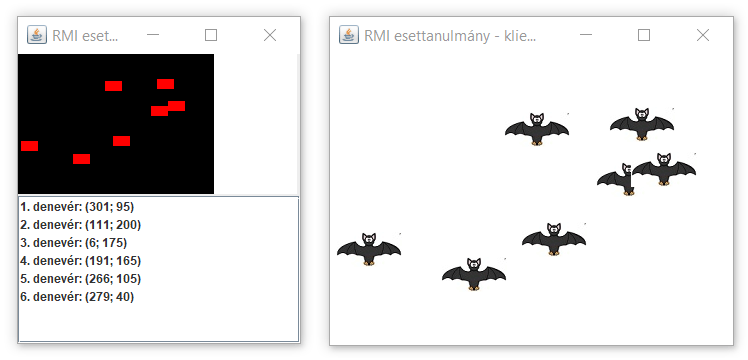
Évekkel ezelőtt hálózatos Java EE esettanulmányt akartunk készíteni Lengyel Borisz kollégával. Ötleteltünk: milyen technológiával és hogyan kommunikáljon egymással a szerver és a kliens(ek). A távoli metódushívás (
