Naprendszer szimuláció – elméleti háttér

Naprendszer szimulációt terveztünk és valósítottunk meg Java nyelven, amit három részből álló blog bejegyzés sorozatban mutatunk be (ez az 1. rész):

Naprendszer szimuláció 1. rész – elméleti háttér
Naprendszer szimuláció 2. rész – objektumorientált tervezés
Naprendszer szimuláció 3. rész – megvalósítás Java nyelven

A Naprendszer szimuláció elméleti háttere

A Naprendszer szimulációhoz elengedhetetlen, hogy ismerjük a homogén koordinátákat, az elemi műveletek egységes megvalósításához szükséges transzformációs mátrixokat, a tömegvonzás elvét és az implementációhoz szükséges MVC modellt.

Homogén koordináták

Számítógépes algoritmusokkal egyszerű a térbeli transzformáció megvalósítása, ha homogén koordinátákat használunk. Segítségükkel az affin transzformációk egységesen kezelhetők. A cél egy egységes matematikai formalizmus alkalmazása. A pontok az égitestek középpontjait fogják jelölni. Legyen a P pont 3D-beli koordinátái: P=(x, y, z). Szükséges egy konstans érték. Ha w≠0, akkor a P pont koordinátái: P=(w·x, w·y, w·z, w). Ha w=1, akkor a P pont normalizált homogén koordinátái: P=(x, y, z, 1). A pontnégyes kijelölése kölcsönösen egyértelmű.

Transzformációk

Koordináta transzformáció során az ábrázolandó grafikus objektum pontjaihoz (tárgypontokhoz) új koordináta-rendszert rendelünk hozzá. Az objektum nem változik (nem torzul, nem változtatja meg az alakját), csupán a nézőpont változik meg. Például: a koordináta-rendszer eltolása, elforgatása, a koordinátatengelyek felcserélése, tükrözése, és a léptékváltás (nagyítás, kicsinyítés, összenyomás, széthúzás), elforgatjuk az ekliptika síkját a szimulált Naprendszerben.

Pont transzformáció esetén a tárgypontokhoz hozzárendeljük azok egy adott szempont szerinti hasonmását. Például: 3D-s tárgyak leképezése 2D-s képre, objektumok eltolása, forgatása, mozgatása, égitestek mozgatása tömegvonzás alapján. Affin transzformációk (egybevágósági és hasonlósági transzformációk) alkalmazása esetén pont képe pont, szakasz képe szakasz, felület képe felület, valamint metsző térelemek eredeti metszésvonala megegyezik azok leképezett metszésvonalával.

A számítógépes grafika területén az affin transzformációk általános alakja (mátrixosan):

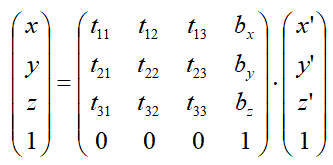
A pont a B=(b_x, b_y, b_z) vektorral eltolható. A pont – a T=(t₁₁, t₁₂, …, t₃₃) mátrixot használva – adott szöggel elforgatható, skálázható, tükrözhető. A számítógépes grafikában ezt a transzformációs mátrixot a homogén koordinátákkal alkalmazva, az összes geometriai transzformáció hatékonyan megvalósítható, visszavezethető mátrixok szorzására. Mindezt saját magunk is implementálhatjuk, de része a DirectX és OpenGL rendering pipeline-jának is.

Más módon is lehetne: egyenes és ehhez tartozó szög párossal is dolgozhatnánk.

A tömegvonzás elve

A tömegvonzás bármely két égitest között meghatározott, függ a gravitációs állandótól és az égitestek tömegétől egyenes arányban, az égitestek (tömeg)középpontjainak távolságától fordított arányban. Ez a Newton szerinti értelmezés, amelynek képlete:

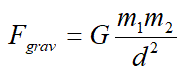
A hatás-ellenhatás törvénye miatt a vonzás – egymás felé való gyorsulás – kölcsönös, a gyorsulás az égitestek tömegével fordítottan arányos, sosem nulla. A Naprendszerben a bolygók a Nap körül keringenek, és a bolygóknak lehetnek holdjaik. Egységesen kezelve: égitestek.

A tömegvonzásnak más elméleti megközelítései is vannak: Einstein gödör-modellje, Kepler törvényei, illetve differenciál-egyenletrendszer, integrálszámítás is használható a közelítő képlet helyett (csak ideális modell esetén pontszerű az égitest és gömbszimmetrikus azok tömegeloszlása), illetve ismeretes többféle értelmezés a rendszer/modell stabilitására: Lagrange pontok, Lyapunov stabilitás.

Az MVC modell

A klasszikus megközelítés szerint a szoftveres alkalmazások három, egymástól jól elkülöníthető szereppel rendelkező egységből állnak: modell (model), nézet (view), vezérlő (controller). A Java nyelv Swing komponensei az MVC architektúra szerint működnek.

A vezérlő reagál az érkező eseményre, hozzáfér a modell adatszerkezeteihez, azaz igénybe veszi a modell szolgáltatásait, valamint frissítheti a nézetet. A nézet a vezérlő frissítési kérésére a közvetlenül megkapott adatok alapján, vagy a modelltől elkért adatok alapján frissíti saját magát. A vezérlő határozza meg az alkalmazás, komponens, program működését. Egy modellt több nézet is használhat. A modell közvetlenül is üzenheti a nézetnek, hogy megváltozott. A nézet adja a látványt, amelyet angolul skin vagy „look and feel”-nek neveznek.