Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.
A 2. évad 8. epizódjában – amelynek címe Fogd a nőt, és fuss! (The Lizard–Spock Expansion) – ismerjük meg a játékszabályt és rögtön alkalmazásra is kerül. Raj és Sheldon megpróbálja eldönteni, hogy melyik sci-fi sorozat a (leg)jobb, illetve Howard és Sheldon így próbálnak osztozni a vacsora maradékán. Végül az 5. évad 17. epizódjában – amelynek címe Itt a festmény, hol a festmény! (The Rothman Disintegration) – újra hallhatjuk a játékszabályt. Ekkor Kripke és Sheldon egy egyetemi iroda sorsáról (kié legyen) próbál dönteni.
A kő-papír-olló-gyík-Spock játékszabály
Vajon hogyan bővül ki a klasszikus kő-papír-olló játékszabálya további két kézjel/fegyver hozzáadásával? Íme a játékszabály videóban:
Az olló elvágja a papírt,
a papír bevonja a követ,
a kő agyonüti a gyíkot,
a gyík megmarja Spockot,
Spock eltöri az ollót,
az olló lefejezi a gyíkot,
a gyík megeszi a papírt,
a papír cáfolja Spockot,
Spock feloldja a követ,
a kő eltöri az ollót.
Ugye mi sem egyszerűbb? 🙂
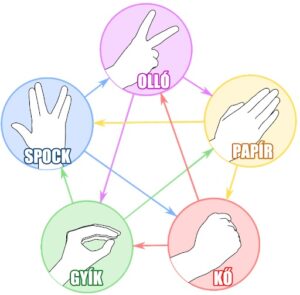
A játékszabálynak számos grafikus ábrázolása is van. Ezeken többnyire irányított gráf csomópontjai mutatják a kézjeleket és a nyilak iránya mutatja, hogy mi mit győz le. Például a gyíktól Spock felé mutató jelzi, hogy a gyík megmarja (azaz legyőzi) Spock-ot. Íme az egyik ábra:
A kő-papír-olló-gyík-Spock játék szimulációja Java programmal
Az objektumorientált tervezés egyik lehetősége az öröklődés beépítése. Közös pontokat, funkcionalitást keresünk. Ezeket beépítjük az ősosztályba és az utódokban kiegészítjük, testre szabjuk. Kiindulunk az alábbi absztrakt Dontes ősosztályból:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
abstract class Dontes { private static final String[] DONTES={ "kő", "papír", "olló", "gyík", "Spock"}; //-1: döntetlen // 0 1 2 3 4 protected static int veletlenDontes() { return (int)(Math.random()*5); //0-4 } private String dontesEredmeny(int d) { return d==-1 ? "döntetlen" : DONTES[d]+ " nyert"; } protected String kiiras(int d1, int d2) { if(d1<-1 || d1>=DONTES.length || d2<-1 || d2>=DONTES.length) throw new IllegalArgumentException("Hiba! Érvénytelen döntés."); return DONTES[d1]+" és "+ DONTES[d2]+": "+ dontesEredmeny(eredmeny(d1, d2)); }; protected int eredmeny(int d1, int d2, int d3) { return eredmeny(d1, eredmeny(d2, d3)); } public abstract int eredmeny(int dontes1, int dontes2); } |
A konstans DONTES tömb (indexelhető adatszerkezet) tárolja a kézjelek/fegyverek elnevezését. Ezek közül választ véletlenszerűen a veletlenDontes() függvény. Az eredményt ki kell tudni írni a konzolra, illetve kezelni kell a döntetlent is. Ezekért közösen felelnek a dontesEredmeny() és a kiiras() függvények. A túlterhelt metódusokként létrehozott eredmeny() függvények kezelik a 2 illetve 3 játékos esetén a döntéseket. A háromparaméteres függvény visszavezet a kétparaméteres esetre. Utóbbi metódus – mivel absztrakt – csak az utódosztályban valósul meg. Így lehetővé válik a játékszabály többféle megvalósítása.
1. megoldás
Az első megoldás során adatszerkezet nélkül valósul meg a játékszabály a KoPapirOlloGyikSpockV1 utódosztályban:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
class KoPapirOlloGyikSpockV1 extends Dontes { @Override public int eredmeny(int d1, int d2) { if(d1==d2) //döntetlen return -1; return (d1==2 && d2==1) || //Az olló elvágja a papírt, (d1==1 && d2==0) || //a papír bevonja a követ, (d1==0 && d2==3) || //a kő agyonüti a gyíkot, (d1==3 && d2==4) || //a gyík megmarja Spockot, (d1==4 && d2==2) || //Spock eltöri az ollót, (d1==2 && d2==3) || //az olló lefejezi a gyíkot, (d1==3 && d2==1) || //a gyík megeszi a papírt, (d1==1 && d2==4) || //a papír cáfolja Spockot, (d1==4 && d2==0) || //Spock feloldja a követ, (d1==0 && d2==2) ? //a kő eltöri az ollót. d1 : d2; } } |
2. megoldás
A második megoldás során a játékszabályt konstansként deklarált MATRIX szomszédsági -, csúcsmátrix, kétdimenziós tömb adatszerkezet tárolja. Ez alapján döntést tud hozni a KoPapirOlloGyikSpockV2 utódosztály.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
class KoPapirOlloGyikSpockV2 extends Dontes { private static final int[][] MATRIX={ // kő papír olló gyík Spock /*kő*/ {0, 0, 1, 1, 0}, //A kő eltöri az ollót, a kő agyonüti a gyíkot, /*papír*/ {1, 0, 0, 0, 1}, //a papír bevonja a követ, a papír cáfolja Spockot, /*olló*/ {0, 1, 0, 1, 0}, //az olló elvágja a papírt, az olló lefejezi a gyíkot, /*gyík*/ {0, 1, 0, 0, 1}, //a gyík megeszi a papírt, a gyík megmarja Spockot, /*Spock*/ {1, 0, 1, 0, 0} //Spock feloldja a követ, Spock eltöri az ollót. }; @Override public int eredmeny(int d1, int d2) { if(d1==d2) //döntetlen return -1; return MATRIX[d1][d2]==1 ? d1 : d2; } } |
A játékmenetért felelős vezérlés
10 lépésből álló játékmenetet hoz létre az alábbi vezérlés:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
public class KoPapirOlloGyikSpock { public static void main(String[] args) { KoPapirOlloGyikSpockV1 jatekV1=new KoPapirOlloGyikSpockV1(); KoPapirOlloGyikSpockV2 jatekV2=new KoPapirOlloGyikSpockV2(); for(int i=1; i<=10; i++) { int d1=Dontes.veletlenDontes(); int d2=Dontes.veletlenDontes(); System.out.println(jatekV1.kiiras(d1, d2)); System.out.println(jatekV2.kiiras(d1, d2)); System.out.println(); } } } |
Egyben tesztelés is: igazolja, hogy azonosan működik a két különböző megoldás.
Eredmény
Mivel minden véletlenszerűen alakul a játékban, ezért az alábbi csupán egy a sokféle lehetséges kimenet közül:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
papír és gyík: gyík nyert papír és gyík: gyík nyert kő és kő: döntetlen kő és kő: döntetlen kő és papír: papír nyert kő és papír: papír nyert Spock és papír: papír nyert Spock és papír: papír nyert olló és Spock: Spock nyert olló és Spock: Spock nyert kő és Spock: Spock nyert kő és Spock: Spock nyert papír és papír: döntetlen papír és papír: döntetlen gyík és Spock: gyík nyert gyík és Spock: gyík nyert gyík és kő: kő nyert gyík és kő: kő nyert gyík és kő: kő nyert gyík és kő: kő nyert |
A bejegyzéshez tartozó teljes forráskódot – többféle változatban is – ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 5-8. óra: Vezérlő szerkezetek, 9-12. óra: Metódusok, rekurzió, 13-16- óra: Tömbök, illetve a 17-24. óra: Objektumorientált programozás 1. és 2. rész alkalmaihoz kötődik.
Balázs: várható még Sheldon-féle cikk a blogban? Az eddigi 3 nagyon ötletes volt.
Az Agymenők kapcsán Balázs: van egy kész anyagunk és két félkész. Örülök, hogy tetszik a téma által inspirált tartalom. Sanyi: publikus ezekkel kapcsolatosan néhány részlet?
Viktor, Balázs: annyi publikus, hogy a kész anyagunk témája a Morse-abc és Sheldon a szemeivel morzézik a hozzá kötődő videóban. Az alkalom (időzítés) kérdéses. Mivel a téma örökzöld, így bármelyik év április elsején megjelenhet. 🙂
Köszönöm mindkettőtöknek. Úgy érzem, érdemes lesz rá várni.
Ez a játékmenet annyira egyszerű, hogy nem is kell hozzá OOP.
Így van Vilmos. Nem feltétlenül kell OO megközelítés. Azonban a kétféle megoldás közös részeit kiemelve jól bemutatható az öröklődés – egyik típusának – működése, megvalósítása: az ősosztály és utódosztály kapcsolata.