Nemzeti pizza nap

Az USA-ban és még néhány országban február 9-én ünneplik a nemzeti pizza napot. Ehhez kötődően kreatív ötletekkel és persze finom pizzákkal vonzzák az éttermek a vendégeket.

Kreatív ötletekkel a mi oktatói csapatunk is rendelkezik. A nemzeti pizza nap inspirált bennünket az alábbi feladat megoldására.

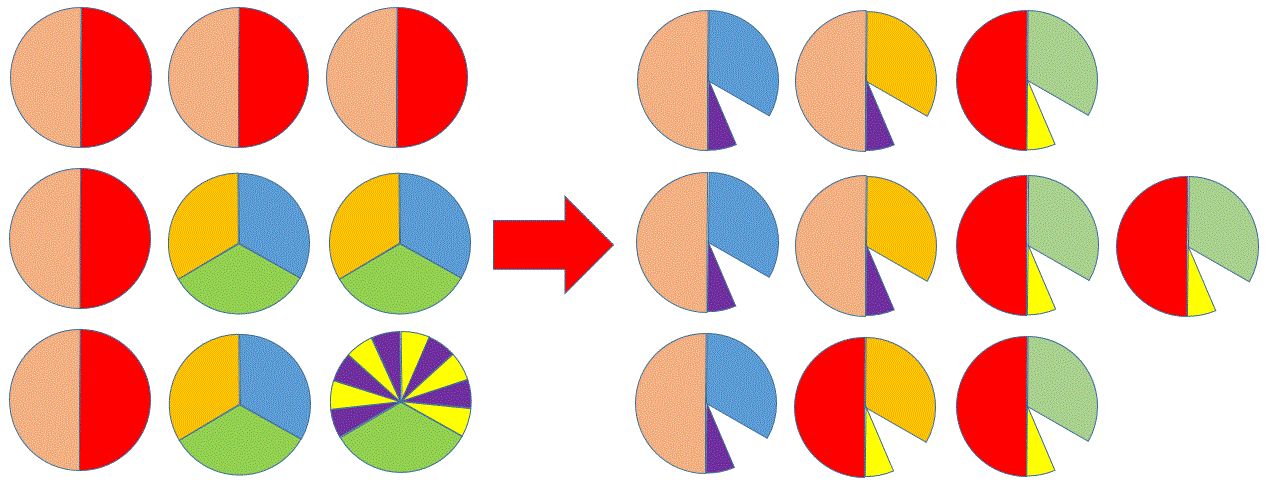
Osszunk szét igazságosan 9 db egyforma pizzát 10 fő között!

Az igazságost úgy értelmezzük, hogy mindenkinek ugyanannyi (ugyanakkora szelet) pizza jut. Két megoldást mutatunk be grafikusan. Ötleteket adunk ahhoz, hogyan programozható le mindez Java nyelven: swing grafikus felületen, grafikai primitívekkel vagy ismert algoritmusokkal. Ábrákkal mutatjuk be a megoldásokat, színekkel kiemelve az azonos/különböző méretű pizzaszeleteket.

1. megoldás

Mind a 9 db pizzából vágjunk ki egytized méretű szeletet. Marad 9 db kilenctized méretű pizzaszelet és a 9 db egytizedből összeállítható a 10. főnek járó szintén kilenctized méretű pizzaszelet/adag.

2. megoldás

A 9 db pizzából 5 db pizzát vágjunk ketté. Keletkezik 10 db fél pizza. A maradék 4 db pizzát harmadoljunk fel. Keletkezik 12 db egyharmad pizza. A keletkező 2 db egyharmad pizzát osszuk fel 5-5 részre. Keletkezik 10 db egytizenötöd méretű pizzaszelet. Az egyharmad ötödrésze adja az egytizenötöd részt. A 10 főnek járó adaghoz rakjuk össze a 30 db részből a különbözőket: egy adag kilenctized, ami egy fél és egy harmad és egy tizenötöd részből áll össze. Másképpen: 9/10 = 27/30 = 15/30 + 10/30 + 2/30.

Ötletek a Java nyelvű megvalósításhoz

• A JFrame osztályból származtatott ablak utódosztály tartalompaneljére ráhelyezhető egy öröklődés útján testre szabott JPanel utódosztályból létrehozott objektum. Ennek van grafikus vászna ( Graphics objektum), amely saját koordináta-rendszerrel és pixelszintű hozzáféréssel rendelkezik. Rendelkezésre áll számos grafikai primitív rajzolására használható metódus, például vonal/szakasz, téglalap, ellipszis. A grafikai primitíveknek rajzolható adott színű körvonala és lehetnek adott színnel kitöltöttek is. Például: drawArc(x, y, width, height, startAngle, arcAngle), vagy az azonos paraméterezésű fillArc(...) metódus. A két szög értelmezése: a startAngle az analóg órán a 3 óra irányába néz, valamint az arcAngle pozitív szög fokban megadva az óramutató járásával ellenkező irányba mutat.
• A beépített grafikus primitívek helyett használhatunk klasszikus algoritmusokat is. Például a Bresenham vonalrajzoló algoritmus, vagy ennek általánosítása a Bresenham körrajzoló (felezőpont) algoritmus. Ezekhez hasznos némi koordináta-geometria és többféle koordináta-rendszer ismerete.

Ötletek továbbfejlesztéshez

• Megpróbálhatjuk általánosítani a problémát: osszunk szét igazságosan n db egyforma pizzát n+1 fő között!
• A statikus képek előállítását követően időzítéssel ellátott animációt is készíthetünk, amely megfelelően mozgatja, forgatja a pizzaszeleteket. Így fázisonként megmutathatók a feladat megoldásának lépései. Ehhez többrétegű vászontechnika szükséges, amelyen könnyen mozgatható a nézőhöz közelebbi réteg úgy, hogy a háttér nem változik meg.
• A saját rajzolt elemek időzítővel – javax.swing.Timer – történő mozgatására példáink java.swing-ben: Hóesés szimuláció és Naprendszer szimuláció – megvalósítás Java nyelven.
• A saját rajzolt elemek kézi – eseménykezelővel megvalósított – mozgatásához felhasználható példánk JavaFX-ben: Kígyókocka grafikus felületen.
• A fázisokból lépésenként vezérelhetően felépülő ábrák elkészítéséhez példáink: Fibonacci-spirál és Koch-görbe rajzolása.

A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

A feladat – a matematikai háttértől eltekintve – a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 21-24. óra: Objektumorientált programozás 2. rész, valamint a 29-36. Grafikus felhasználói felület alkalmaihoz kötődik.

Ajánljuk a Java SE szoftverfejlesztő tanfolyam kategóriából