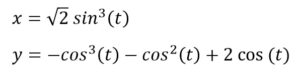A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
PDF fájl többféleképpen is készíthető. Például:
- irodai szoftverek Mentés másként… menüpontjában,
- Adobe Acrobat szoftverrel,
- online alkalmazásokkal sokféle fájlformátum konvertálható PDF-be,
- speciális célszoftverek is generálhatnak PDF fájlokat.
Utóbbi esetekre néhány példa:
- online megvásárolt koncertjegyet e-mail csatolmányaként kapunk PDF-ben, ugyanígy számlát is róla,
- online tanfolyamunk záró tesztjét követően letölthető tanúsítványt, badge-t, online IQ tesztünk eredményeként oklevelet kapunk PDF fájlként,
- kérdőívek kitöltése során egyéni válaszainkat visszaigazolásként PDF-et kapunk, vagy a kérdőív kitöltési időszakának végén összesített eredményt, PDF riportot kapunk.
Java program készít PDF fájlt
Adatokra van szükség. Korábbi Munkakör, létszám, névsor lekérdezése blog bejegyzésünkben az Oracle HR sémából kétféleképpen is lekérdeztük a szükséges adatokat. Ezt érdemes előzetesen tanulmányozni, hogy a további tartalom könnyebben érthető legyen. A Java SE szoftverfejlesztő tanfolyam megközelítése alapján, az egyszerűbb SQL paranccsal előállított eredménytáblát a PDF generálása előtt még csoportosítani kell (munkakörönként). A Java adatbázis-kezelő tanfolyam megközelítése alapján, az összetettebb SQL paranccsal elkészített, denormalizált eredménytábla közvetlenül felhasználható.
A cél egy táblázat elkészítése, amely 3 oszlopból áll: munkakör, létszám és névsor. Az azonos munkakörű alkalmazottak névsora egy táblázat egyetlen cellájában legyen megjeleníthető. Az elkészült táblázatból készüljön PDF fájl.
A teendők lépésenként
Szükséges az iText csomag importálása:
com.itextpdf.text. Korábbi változata az 5-ös, aktuális változata a 8-as. Előbbi nagyon elterjedt, utóbbi még kevésbé ismert. A továbbiakban a kötelező kivételkezeléshez kötődő forráskód-részletek bemutatásától eltekintünk.
Tehát adott az összes szükséges adat egy
ArrayList<MunkakorLetszamNevsor> lista generikus listában. A POJO mindhárom szükséges és összetartozó tulajdonságot tárolja:
String munkakor,
int letszam,
String nevsor.
Hasznos egy általánosan használható
cella() függvény elkészítése, amely képes adott szöveget, adott betűmérettel, adott betűstílussal, adott igazítással „megjeleníteni”:
|
|
private PdfPCell cella(String szoveg, int betumeret, boolean felkover, int igazitas) throws DocumentException, IOException { PdfPCell cella=new PdfPCell(); BaseFont betutipus=BaseFont.createFont( BaseFont.HELVETICA, BaseFont.CP1250, BaseFont.EMBEDDED); Paragraph bekezdes=new Paragraph(szoveg, new Font(betutipus, betumeret, felkover?Font.BOLD:Font.NORMAL)); bekezdes.setAlignment(igazitas); cella.addElement(bekezdes); cella.setPadding(2); cella.setVerticalAlignment(Paragraph.ALIGN_CENTER); return cella; } |
Létre kell hozni a
pdfFajl objektumot, beállítani a méretét és a margókat, illetve fájlba kell irányítani:
|
|
Document pdfFajl=new Document(PageSize.A4, 15, 15, 30, 20); PdfWriter.getInstance(pdfFajl, new FileOutputStream("./files/jelentes.pdf")); pdfFajl.open(); |
Létre kell hozni a táblázat előtt megjelenő szöveget (ez nem a szövegszerkesztés szerinti valódi fejléc):
|
|
BaseFont betutípus=BaseFont.createFont( BaseFont.HELVETICA, BaseFont.CP1250, BaseFont.EMBEDDED); Paragraph fejlec= new Paragraph("Jelentés", new Font(betutípus, 20, Font.BOLD)); fejlec.setAlignment(Paragraph.ALIGN_CENTER); pdfFajl.add(fejlec); |
Létre kell hozni a táblázatot, megfelelő beállításokkal:
|
|
PdfPTable tablazat=new PdfPTable(3); tablazat.setWidthPercentage(85); tablazat.setSpacingBefore(40); tablazat.setWidths(new float[] {0.2f, 0.1f, 0.7f}); |
Létre kell hozni a táblázat fejlécét:
|
|
tablazat.addCell( cella("Munkakör", 14, true, Paragraph.ALIGN_CENTER)); tablazat.addCell( cella("Lét-\nszám", 14, true, Paragraph.ALIGN_CENTER)); tablazat.addCell( cella("Névsor", 14, true, Paragraph.ALIGN_CENTER)); |
Végig kell haladni az adatokon és elő kell állítani a szükséges táblázatcellákat, végül le kell zárni a fájlt:
|
|
for(MunkakorLetszamNevsor mln: lista) { tablazat.addCell( cella(mln.getMunkakor(), 12, false, Paragraph.ALIGN_LEFT)); tablazat.addCell( cella(""+mln.getLetszam(), 12, false, Paragraph.ALIGN_CENTER)); tablazat.addCell( cella(mln.getNevsor(), 12, false, Paragraph.ALIGN_LEFT)); } pdfFajl.add(tablazat); pdfFajl.close(); |
A PDF fájl és a belekerülő táblázatobjektum szerkezete DOM-szerű, illetve azonos a grafikus felhasználói felület felépítése során használt AWT/swing konténerszemlélettel.
A felhasznált programozási tételek: sorozatszámítás, kiválasztás, megszámolás, kiválogatás, illetve kombináltan: csoportosítás, rendezés.
Az eredmény
Az elkészült PDF fájl másfél oldalas, itt letölthető, megtekinthető. A dokumentumról készült képernyőkép:

Továbbfejlesztési lehetőségek
Igényeinktől függően, illetve előzetes tapasztalatainkra és a meglévő tudásunkra építve számos ötlet merülhet fel. Mindhárom tanfolyam esetén testre tudjuk szabni azt az SQL parancsot, ami a szükséges adatokat lekérdezi. Az iText csomag helyett felfedezhetjük a PDF Clown, a PDFBox, illetve a Spire.PDF csomagok funkcionalitását is.
- A Java SE szoftverfejlesztő tanfolyam tematikájához kötődve egyszerűbb dolgokat tudunk megvalósítani. Használhatunk további stílusokat: betűre, bekezdésre, cellára, táblázatra vonatkoztatva, színeket, szegélyeket. Többoldalas dokumentum esetén hozzáadhatunk oldalszámot, oldalszám / oldalak száma mezőt, tényleges fej- és láblécet, generálásra vonatkozó időbélyeget, képezhetjük szabály alapján a PDF fájl nevét, illetve tallózhatjuk annak helyét (hol jöjjön létre).
- A Java EE szoftverfejlesztő tanfolyam tematikájához kötődve az előzőeken felül elhelyezhetjük a generált fájlt egy szerveren és elküldhetjük e-mailben a letöltéséhez szükséges URL-t. A letöltés korlátozható darabszámmal és időben is (például max. 3 db letöltés lehetséges a következő 48 órán belül). A PDF fájlba belekerülhet szöveges vízjel, céges logó és saját képként dinamikusan előállított grafikon. Például a JFreeChart grafikon készítése projekt swing-es GUI felületéből néhány utasítással készíthetünk JPG vagy GIF formátumú képet, ami könnyen beilleszthető PDF-be. Online, webes API szolgáltatás használatával az előállított PDF fájl tömöríthető, illetve belekerülhet QR kód, vonalkód is.
- A Java adatbázis-kezelő tanfolyam tematikájához kötődve az előzőeken felül a JDBC alapú back-end kicserélhető JPA alapúra. A PDF láblécébe beleírhatjuk, hogy az adatbázis-szerveren kinek a nevében futott (DB User) az a lekérdezés, ami előállította a szükséges adatokat. Megoldható a generált PDF egyedi azonosítója, azaz kétszer nem állítható elő „ugyanaz”. Modulárisan továbbfejlesztve gyakorolhatjuk a tudatosan felépített MVC architekturális tervezési minta használatát. Limit feletti méretű PDF fájlt több kisebbre szétdarabolhatunk.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.








 A
A 
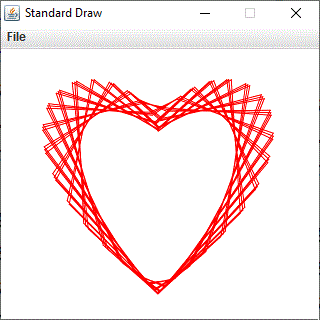
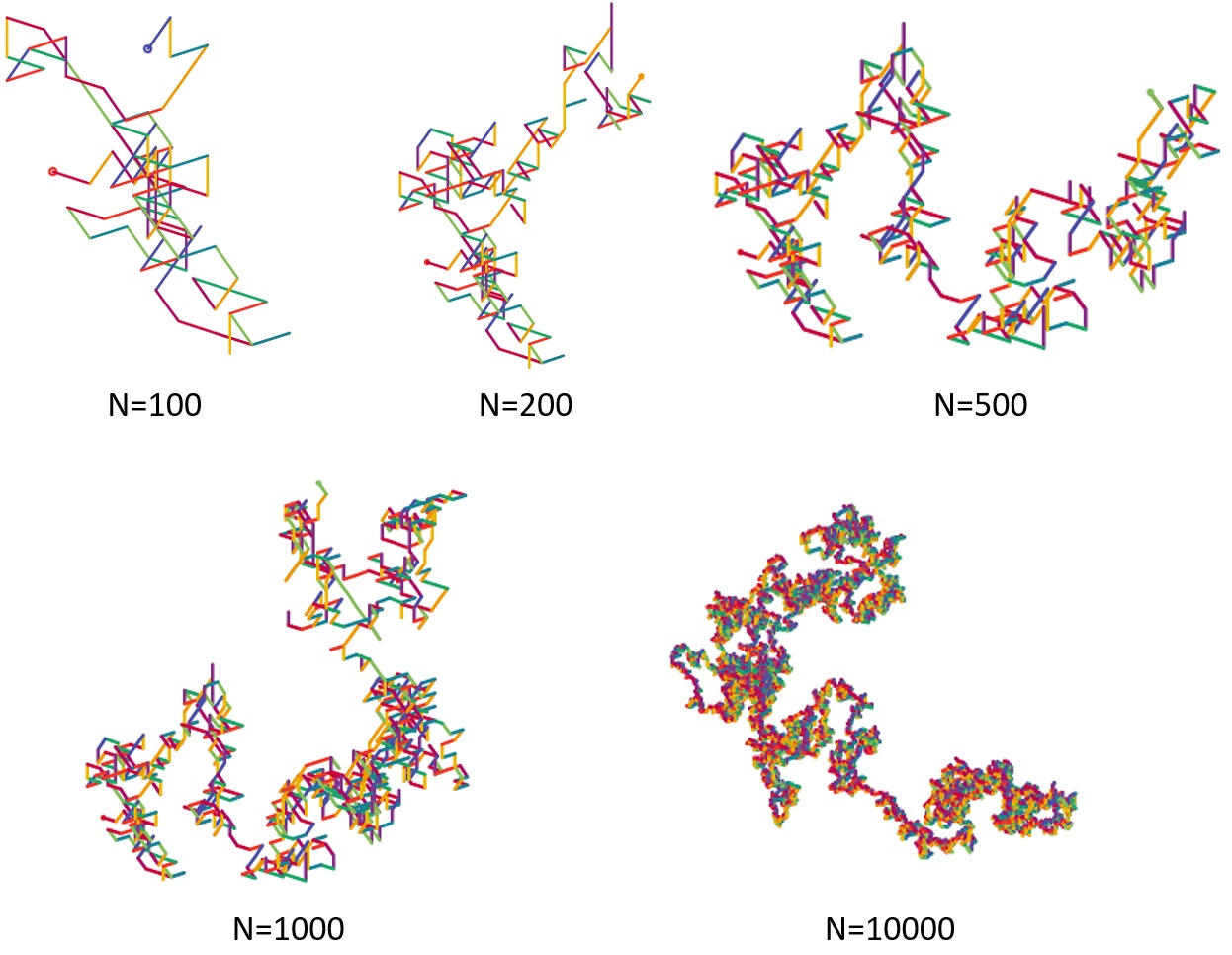
 Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.
Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.
 A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
 A
A 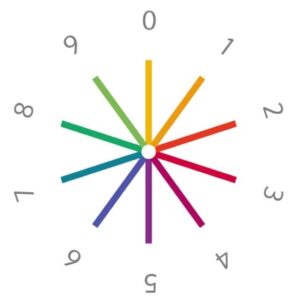
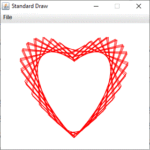 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.