Címke: szimuláció
10 blog bejegyzésnél szerepel:
 Dr. Sheldon Cooper kő-papír-olló-gyík-Spock játéka
Dr. Sheldon Cooper kő-papír-olló-gyík-Spock játéka
 Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
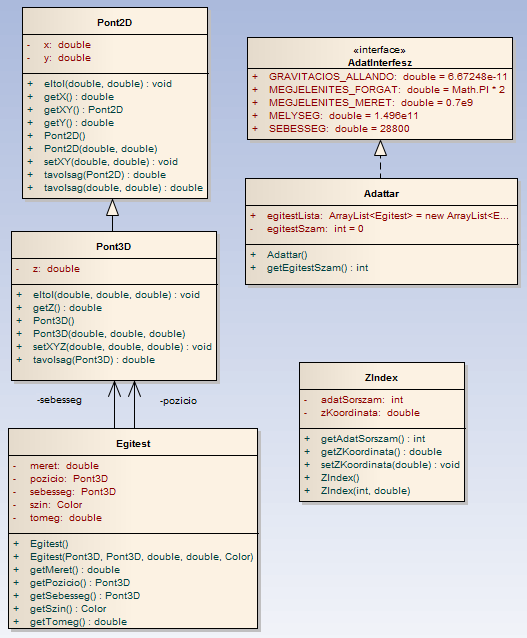
 Naprendszer szimuláció – megvalósítás Java nyelven
Naprendszer szimuláció – megvalósítás Java nyelven
 Naprendszer szimuláció – objektumorientált tervezés
Naprendszer szimuláció – objektumorientált tervezés
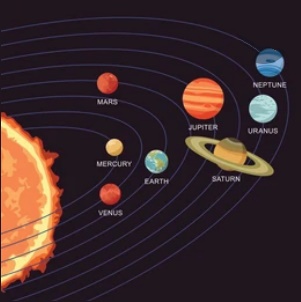
 Naprendszer szimuláció – elméleti háttér
Naprendszer szimuláció – elméleti háttér
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017
116 db hozzá kapcsolódó címke:
2017 (24), 2019 (24), 2021 (24), 2022 (24), 2023 (24), 2024 (8), Agymenők (3), algoritmus (31), állásinterjú (10), álláskeresés (17), animáció (17), atipikus megoldás (5), becslés (6), ChatGPT (1), ciklusok (18), csoportmunka (10), DUF (3), Dunaújvárosi Főiskola (3), élményalapú tanulás (21), előadás műhely-napon (24), elosztott alkalmazás (14), érettségi feladat (8), fájlkezelés (29), fizika (7), funkcionális programozás (18), gamifikáció (33), GitHub (2), Google Cloud Platform (2), grafika (26), grafikus felhasználói felület (40), hatékonyság (28), humor (4), időzítő (4), IEEE Spectrum (2), Indeed (2), ingyenes esemény (34), ipar 4.0 (6), ipar 5.0 (2), játék (9), Java forráskód (63), JavaScript (6), karrier (17), karrierváltás (14), kivételkezelés (13), kliens-szerver (7), kliensprogram (13), kockadobás (1), kollekció (32), kombinatorika (7), közelítés (3), kriptoaritmetika (2), Kutatók éjszakája (8), LEGO (3), lépésszám (9), logikai feladat (21), logisztika (5), lottószelvény (10), matematika érettségi feladat (8), matematika (30), mém (7), mesterséges intelligencia (12), metódus (30), munkaerőpiac (14), MVC (12), Naprendszer (5), NASA (2), nyári tábor (2), okos gyár (5), objektumorientált programozás (85), OpenWeatherMap (2), optikai csalódás (2), orientáló modul (39), öröklődés (16), összefoglalás (2), osztálydiagram (7), pályaorientáció (28), pályázat (6), ProgCont API (3), programozás (106), programozási tételek (28), projektmunka (5), protokoll (számítógép-hálózat) (3), PYPL (2), Python (4), rajzolás (15), Reddit (2), rekurzió (9), rendezvény 2023 (10), robotika (12), robotprogramozás (11), soft skill (10), Stack Overflow (2), statisztika (11), STEM (3), swing (26), szakmai előadás (31), szakmai modul (96), szálkezelés (4), sztereogram (1), tananyagfejlesztés (8), tervezés (41), tesztelés (21), tévésorozat (3), TIOBE (2), tipikus munkanap (6), többféle megoldás összehasonlítása (37), tömb (17), tömegvonzás (5), továbbfejlesztés (23), transzformáció (8), Trendy Skills (2), UML (8), vélemény (4), videó (5), virtuális valóság (5), visszajelzés (5)





 Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.
Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.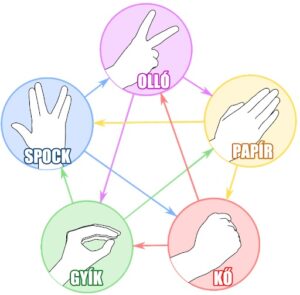


 A STEM mozaikszó eléggé közismert: a tudományos-technológiai tudományágakat (természettudomány, technológia, mérnöki tudomány és matematika) foglalja egybe, interdiszciplináris megközelítésben. A STEM területén való elmélyedés során a hangsúly nem a mit tanulunk/tanítunk, hanem inkább a hogyan tanulunk/tanítunk. Nem azonnal ad kézzel fogható válaszokat, de kitartó próbálkozással – saját élménnyel – elérhető az eredmény.
A STEM mozaikszó eléggé közismert: a tudományos-technológiai tudományágakat (természettudomány, technológia, mérnöki tudomány és matematika) foglalja egybe, interdiszciplináris megközelítésben. A STEM területén való elmélyedés során a hangsúly nem a mit tanulunk/tanítunk, hanem inkább a hogyan tanulunk/tanítunk. Nem azonnal ad kézzel fogható válaszokat, de kitartó próbálkozással – saját élménnyel – elérhető az eredmény.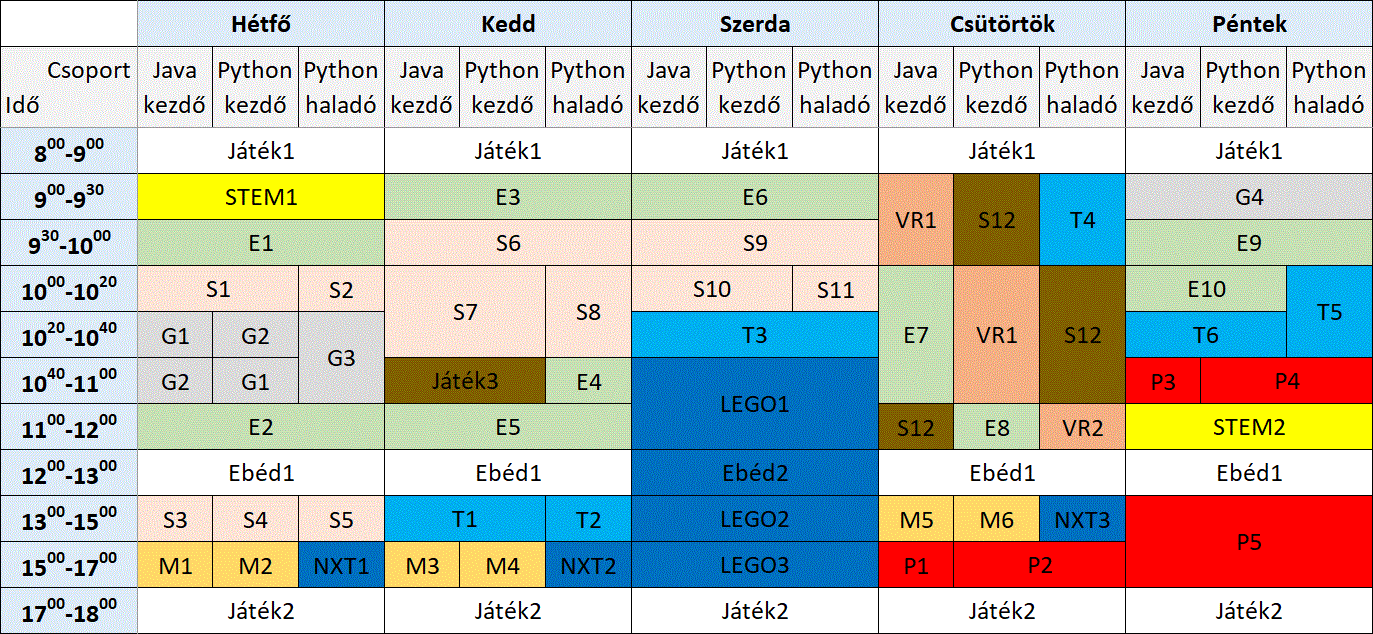
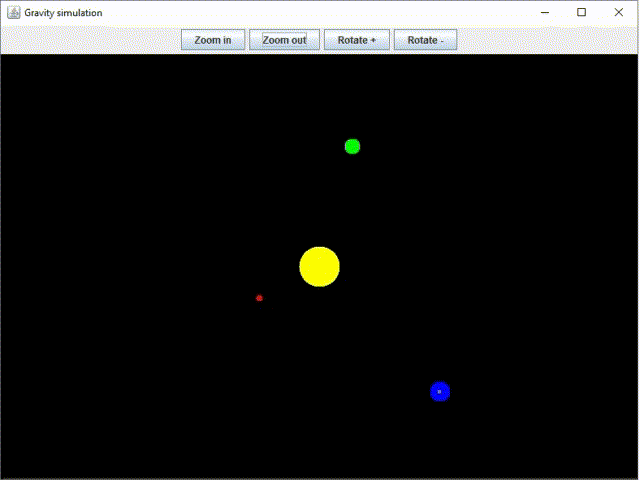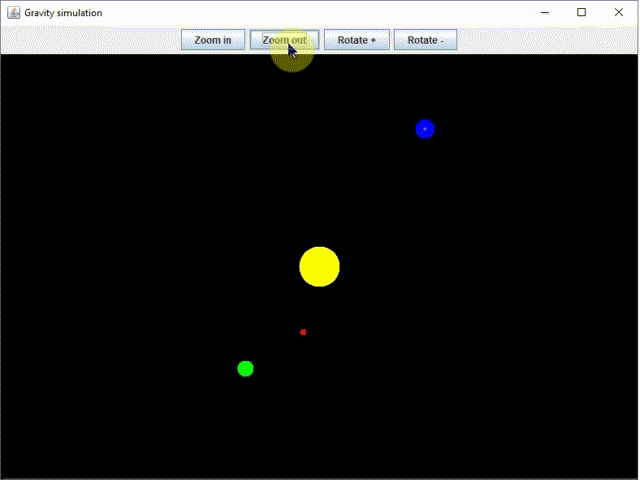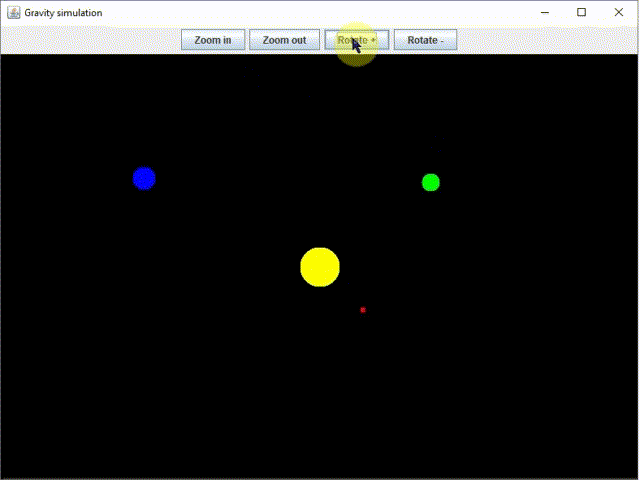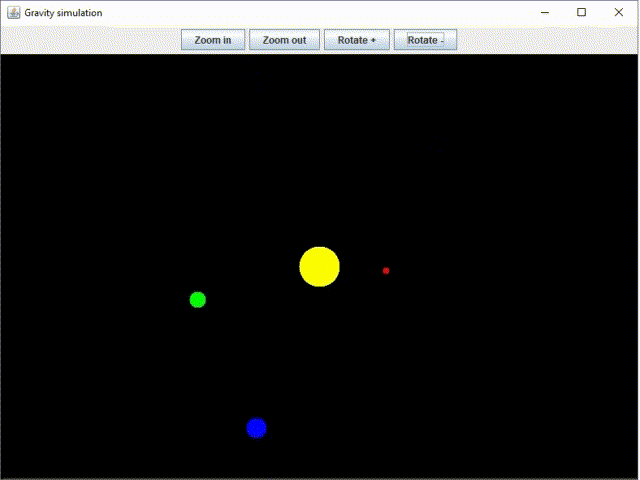
 Naprendszer szimulációt terveztünk és valósítottunk meg Java nyelven, amit három részből álló blog bejegyzés sorozatban mutatunk be (ez a 3. rész):
Naprendszer szimulációt terveztünk és valósítottunk meg Java nyelven, amit három részből álló blog bejegyzés sorozatban mutatunk be (ez a 3. rész):