Címke: többféle megoldás összehasonlítása
37 blog bejegyzésnél szerepel:
 Dr. Sheldon Cooper kő-papír-olló-gyík-Spock játéka
Dr. Sheldon Cooper kő-papír-olló-gyík-Spock játéka
 Kölcsönös ajándékozás véletlenszerűen
Kölcsönös ajándékozás véletlenszerűen
 Kép élesítése effektus működése
Kép élesítése effektus működése
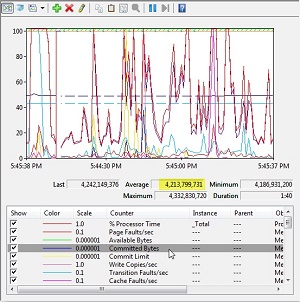 Java program memória használatának mérése
Java program memória használatának mérése
 Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
 Alkalmazottak életpálya modellje – mi lenne, ha…?
Alkalmazottak életpálya modellje – mi lenne, ha…?
 Egy matematika érettségi feladat megoldása programozással 2023
Egy matematika érettségi feladat megoldása programozással 2023
 Egy matematika érettségi feladat megoldása programozással 2022
Egy matematika érettségi feladat megoldása programozással 2022
 Kik vettek részt projektmunkában?
Kik vettek részt projektmunkában?
 Egy matematika érettségi feladat megoldása programozással 2021
Egy matematika érettségi feladat megoldása programozással 2021
 Top 5 fizetésű alkalmazottak listája
Top 5 fizetésű alkalmazottak listája
 Egy matematika érettségi feladat megoldása programozással 2019
Egy matematika érettségi feladat megoldása programozással 2019
 Stream API lambda kifejezésekkel
Stream API lambda kifejezésekkel
 Ismerkedjünk lambda kifejezésekkel!
Ismerkedjünk lambda kifejezésekkel!
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017
177 db hozzá kapcsolódó címke:
2017 (24), 2018 (24), 2019 (24), 2020 (24), 2021 (24), 2022 (24), 2023 (24), 2024 (8), ADA konferencia (2), adatbázis (25), Agymenők (3), algoritmus (31), alkalmazottak életpálya modellje (3), alkalmazottak fizetése (4), alkalmazottak munkaköre (6), állásinterjú (10), álláskeresés (17), animáció (17), Applet (1), ASCII (6), atipikus megoldás (5), becslés (6), brute force (7), C# forráskód (2), ChatGPT (1), ciklusok (18), csoportmunka (10), csoportváltás (6), dátumkezelés (10), DE (3), Debreceni Egyetem (3), életpálya modell (3), élményalapú tanulás (21), előadás műhely-napon (24), elosztott alkalmazás (14), eredménytábla (10), érettségi feladat (8), euklideszi algoritmus (1), Euler (3), évforduló (24), fájlkezelés (29), fejtörő (11), felvételi feladat (4), Fibonacci (3), fizika (7), funkcionális programozás (18), Gábor Dénes Főiskola (1), gamifikáció (33), GDF (1), GitHub (2), Google Charts (5), Google Cloud Platform (2), grafika (26), grafikus felhasználói felület (40), hálózatkezelés (14), hatékonyság (28), hierarchikus lekérdezés (7), humor (4), időzítő (4), IEEE Spectrum (2), Indeed (2), ingyenes esemény (34), ipar 4.0 (6), ipar 5.0 (2), játék (9), Java forráskód (63), JavaFX (3), JavaScript (6), JDBC (12), JSP (3), JTree (6), karrier (17), karrierváltás (14), képeffektus (1), kivételkezelés (13), kliens-szerver (7), kliensprogram (13), kockadobás (1), kollekció (32), kombinatorika (7), konferencia (15), közelítés (3), kriptoaritmetika (2), Kutatók éjszakája (8), lambda kifejezés (13), leghosszabb közös részsorozat (1), legnagyobb közös osztó (1), LEGO (3), lekérdezés (18), lépésszám (9), logikai feladat (21), logisztika (5), lottószelvény (10), MAFIOK (1), matematika érettségi feladat (8), matematika (30), mém (7), memória használat (3), mesterséges intelligencia (12), metódus (30), MMO (6), Multimédia az oktatásban konferencia (6), munkaerőpiac (14), MVC (12), Naprendszer (5), naptár (26), NASA (2), Neumann János Számítógép-tudományi Társaság (8), NJSZT Multimédia az oktatásban (6), NJSZT (8), nyári tábor (2), okos gyár (5), objektumorientált programozás (85), OpenWeatherMap (2), optikai csalódás (2), Oracle HR séma (12), orientáló modul (39), öröklődés (16), összefoglalás (2), osztálydiagram (7), pályaorientáció (28), pályázat (6), PDF (1), péntek 13 (1), Pi nap (2), Pi (2), ProgCont API (3), programozás (106), programozási tételek (28), projektmunka (5), publikáció (9), PYPL (2), Python (4), rajzolás (15), Ratkó István emlékest (1), Reddit (2), rekurzió (9), rendezvény 2018 (10), rendezvény 2019 (11), rendezvény 2021 (6), rendezvény 2022 (8), rendezvény 2023 (10), RMI (3), robotika (12), robotprogramozás (11), Servlet (1), soft skill (10), SQL forráskód (12), Stack Overflow (2), statisztika (11), STEM (3), Stream API (14), swing (26), szakmai előadás (31), szakmai modul (96), szimuláció (10), sztereogram (1), táblázat (11), tananyagfejlesztés (8), tervezés (41), tesztelés (21), tévésorozat (3), TIOBE (2), tipikus munkanap (6), tömb (17), tömegvonzás (5), toplista (5), továbbfejlesztés (23), transzformáció (8), Trendy Skills (2), UML (8), ünnepnap (13), vélemény (4), videó (5), virtuális valóság (5), visszajelzés (5), XML (8)


















 Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.
Dr. Sheldon Cooper karakterét nem kell bemutatni. Ha a kockáknak döntéseket kell hozniuk, akkor az Agymenők (The Big Bang Theory) sorozatban többször is előkerül a kő-papír-olló-gyík-Spock játék.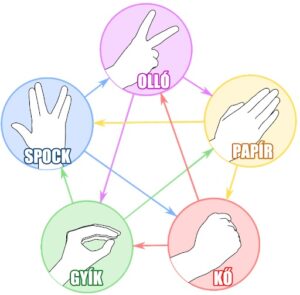
 A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
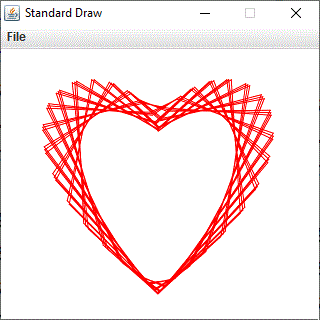
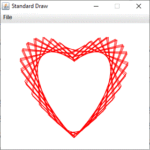 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.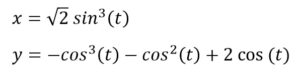



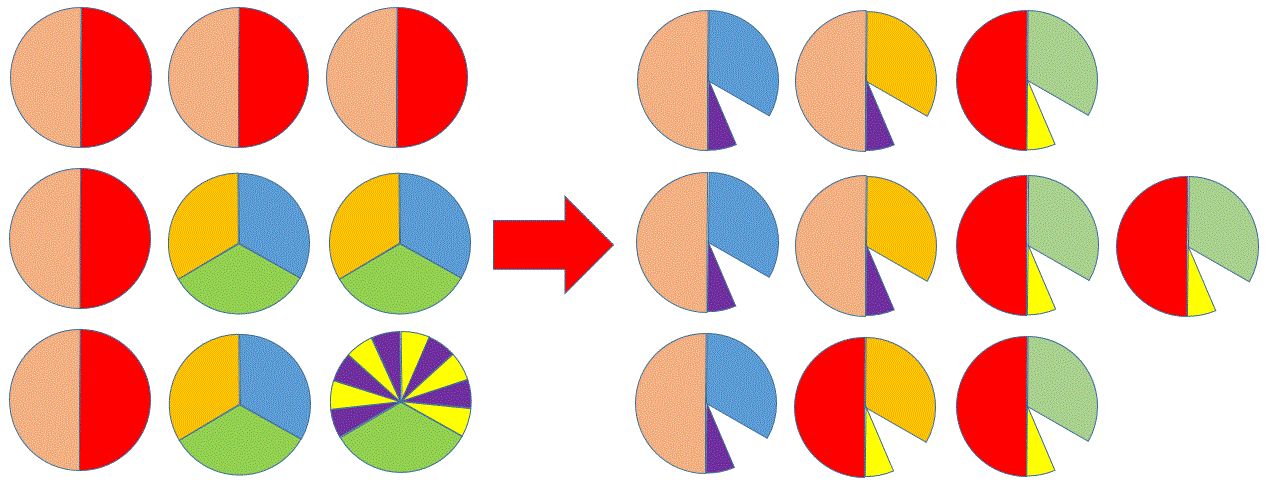
 A kölcsönös ajándékozás időről-időre több közösségben is felmerül. Munkahelyi környezetben és iskolai csoportokban is (például: Télapó, karácsony). Hagyományos megközelítésben így hangzik a szabály: „húzzunk neveket a kalapból”. Másképpen: mindenki 1 ajándékot ad, mindenki 1 ajándékot kap és a sorsolás véletlenszerűen történik.
A kölcsönös ajándékozás időről-időre több közösségben is felmerül. Munkahelyi környezetben és iskolai csoportokban is (például: Télapó, karácsony). Hagyományos megközelítésben így hangzik a szabály: „húzzunk neveket a kalapból”. Másképpen: mindenki 1 ajándékot ad, mindenki 1 ajándékot kap és a sorsolás véletlenszerűen történik.