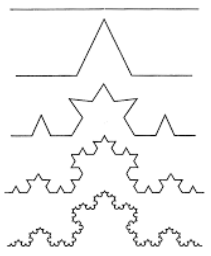
Koch-görbe rajzolása - it-tanfolyam.hu

A Koch-görbe egyike a legrégebben ismert egyszerű fraktáloknak. Mint ilyen, önhasonlóan rekurzív. Az önhasonlóság azt jelenti, hogy az ábra tetszőleges részét felnagyítva mindig hasonló/ugyanolyan részek jelennek meg (a méretaránytól függetlenül). Az n=1 szinten a Koch-görbe kiindulópontja egy szabályos háromszög. A n+1-edik szinten az n-edik szinten található szakaszokat harmadoljuk, és a középső szakasz helyére egy harmad akkora háromszög két szárát illesztjük (az alapját kihagyjuk). Ezt rekurzívan folytatva kapjuk meg a Koch-görbét, másképpen Koch-féle hópelyhet.

Írtam egy egyszerű Java programot, amely n=1-től 9-ig paraméterezhetően kirajzolja a Koch-görbét egy grafikus felületre. Így működik:

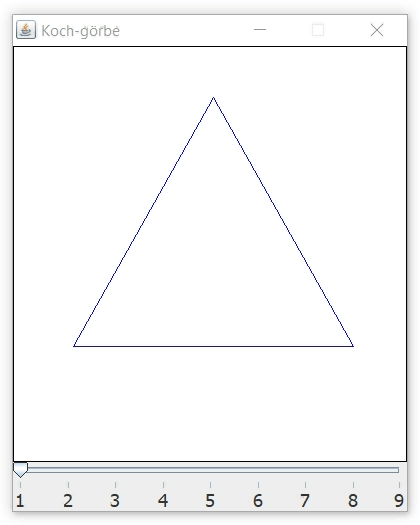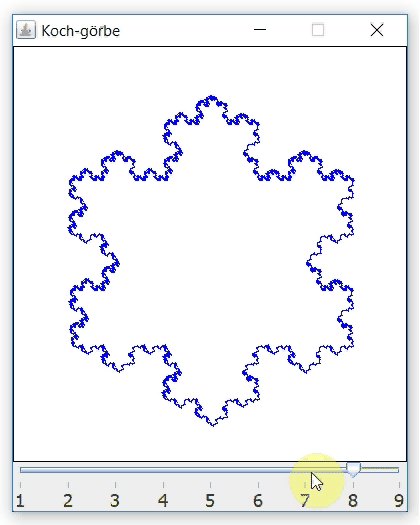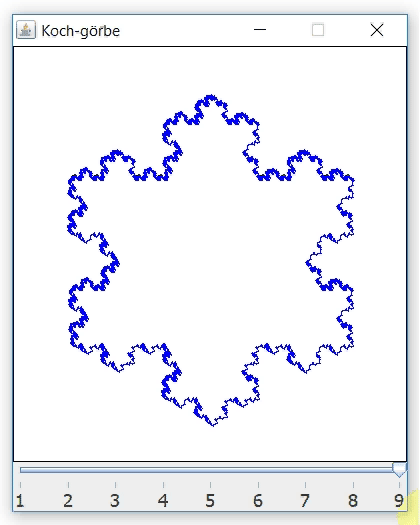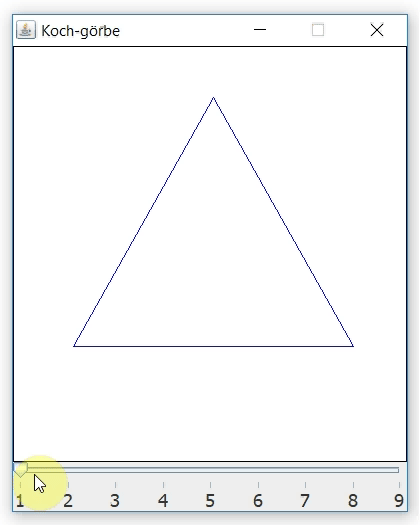
A program elkészítéséhez néhány alapvető dolgot kell csupán tudni:

Vászontechnikával tudunk swing GUI felületre ( Graphics osztályú g objektum) rajzolni, ahol a koordináta-rendszer origója egy téglalap alakú terület bal felső csúcsa, X jobbra növekszik, Y pedig lefelé növekszik.
Kétféle szín áll rendelkezésre: háttérszín (most Color.WHITE), illetve rajzolószín (most Color.BLUE).
A rajzoláshoz grafikai primitíveket használhatunk, például pont, szakasz, téglalap, ellipszis. Szakaszt két végpontjának koordinátáival tudunk rajzolni a drawLine() metódussal.
Be kell állítani a vászon méreteit, azaz annak a komponensnek ( JPanel-ből öröklött KochPanel osztályú pnKoch objektum) a méreteit, amelyre ráfeszül a vászon.
Egy Slider osztályú sSzint nevű vezérlőobjektum ChangeListener figyelőinterfész stateChanged() eseménykezelő metódust implementáló objektumával paraméterezzük a rajzolást 1-től 9-ig.
A pnKoch objektumnak küldött repaint() üzenet/metódushívás meghívja a felüldefiniált paintComponent() metódust.

@Override

protected void paintComponent(Graphics g) {

super.paintComponent(g);

g.setColor(Color.BLUE);

koch(n, 200, 51, 60, 300, g);

koch(n, 60, 300, 340, 300, g);

koch(n, 340, 300, 200, 51, g);

}

A szakasz négy darab harmad akkora szakaszra osztását a megfelelően paraméterezett rekurzív metódushívások oldják meg az alábbi lépéseket követve:

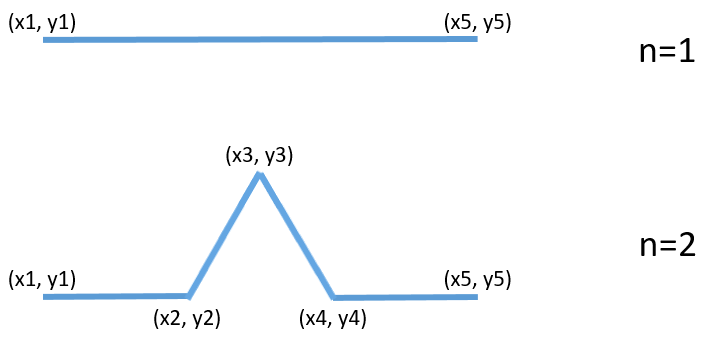
A rekurzív rajzolást a koch() metódus végzi el, ahol a fraktál szabályának megfelelően szakaszharmadolás és a szükséges pontok koordinátáinak (szakaszok végpontjai) kiszámítása történik:

private void koch(int n, int x1, int y1, int x5, int y5, Graphics g) {

if(n==1)

g.drawLine(x1, y1, x5, y5);

else {

double gy=Math.sqrt(3)/6;

int dx=x5-x1, dy=y5-y1,

x2=x1+dx/3, y2=y1+dy/3,

x3=(int)((x1+x5)/2+gy*(y1-y5)), y3=(int)((y1+y5)/2+gy*(x5-x1)),

x4=x1+dx*2/3, y4=y1+dy*2/3;

koch(n-1, x1, y1, x2, y2, g);

koch(n-1, x2, y2, x3, y3, g);

koch(n-1, x3, y3, x4, y4, g);

koch(n-1, x4, y4, x5, y5, g);

}

A Koch-görbének van néhány érdekes tulajdonsága:

kerülete minden rekurzív lépésben minden határon túl növekszik, azaz a végtelenhez tart,
területe véges, hiszen minden rekurzív lépésben belefér a háromszög köré írható körbe,
dimenziója tört, ~ 1,261859.

A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió alkalomra építő 29-36. Grafikus felhasználói felület alkalomhoz kötődik.