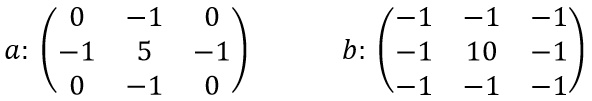Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Lássuk, hogyan valósítható meg Java programozási nyelven a kép élesítése!
A kép adatszerkezete
Adott egy képfájl. Formátuma a tipikus, feldolgozhatók (JPG, GIF, PNG, WebP) egyike. Ezek rasztergrafikus képformátumok. Lekérdezhető a dimenziója: ez képpontban (pixelben) jelenti a kép szélességét (width) és a kép magasságát (height). A vászontechnika meghatározza a kép origóját (0, 0) és a képpontok kétdimenziós koordinátapárját. A kép origója a bal felső sarokban van. A kép oszlopai (column) jobbra haladva növekvő módon, a kép sorai (row) lefelé haladva növekvő módon számozottak. Egy pixel koordinátapárja (c, r) alakban írható le. Minden pixel három szín kombinációjaként áll elő (r, g, b). Másképpen: a piros, zöld és kék összetevők aránya alapján meghatározott. A tipikus színmélység alapján a színek külön-külön 256-félék lehetnek, és ezeket 0-tól 255-ig egész szám képviseli. A 0 az adott szín hiányát, a 255 a szín teljes intenzitását jelenti.
A kép élesítéséhez használható szűrőmátrixok
A kép élesítése során szűrőt alkalmazunk a kép belső pixeleire. A kép 4 szélén lévő pixeleket nem változtatjuk. Többféle szűrő közül választhatunk, íme két példa:
A három színösszetevőre külön-külön kell alkalmazni a szűrőt. Az aktuális pixel – amire alkalmazzuk a szűrőt – a 3×3-as mátrix középső eleméhez igazítva szorzóértékeket tartalmaz. A konkrét eset: az a mátrix esetén az 5 érték a 2. sor 2. oszlopában helyezkedik el; ennek a közvetlen szomszédos pixeleire a -1 értékek, átlós szomszédaira pedig a 0 értékek vonatkoznak. Eredményül a szűrt pixel színeit kapjuk meg külön-külön. Ha a kapott értékek kisebbek 0-nál, akkor nullázzuk őket. Ha a kapott értékek nagyobbak 255-nél, akkor beállítjuk azokat 255-re. Az a szűrőmátrix kevésbé élesít, a b szűrőmátrix erősebben élesít.
Természetesen sok más képélességhez köthető szűrő is van még. Olyanok is vannak, ahol nem csak a közvetlen szomszédos pixeleket veszi figyelembe az algoritmus. További kulcsszavak a témához kötődően: digitális képfeldolgozás, lokális operátor, korreláció, konvolúció, átlagszűrő, mediánszűrő, zajszűrő, Laplace-szűrő.
A kép élesítését megvalósító Java forráskód-részlet
A fenti a mátrixot a
SHARP_FILTER konstans kétdimenziós tömb tárolja. A paraméterként átvett
BufferedImage típusú
img1 objektum kép pixeleinek végigjárását ütközőként segíti a
w szélesség és
h magasság. A
data egydimenziós tömb sorfolytonosan tárolja a kép pixeleit. Az
if elágazó utasítás igaz ága kezeli a kép 4 szélét (változatlanul hagyott másolt színek). Az
if hamis ága a belső pixelekre alkalmazza a szűrőmátrixot. A
red,
green,
blue változók tartalmazzák az aktuális pixel színeit, amelyekbe az eredeti pixelre alkalmazott szűrő által szorzott értékek kerülnek, „belekényszerítve” a 0-255 zárt intervallumba. Végül az eredményül visszaadott
img2 kép pixelei kerülnek beállításra. Az alábbi
sharpenEffect() függvény mindezt megoldja az alábbiak szerint:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
public static BufferedImage sharpenEffect(BufferedImage img1) { final int[][] SHARP_FILTER={ { 0, -1, 0}, {-1, 5, -1}, { 0, -1, 0} }; Color[][] colorArray=new Color[3][3]; int w=img1.getWidth(), h=img1.getHeight(), i=0; int[] data=new int[w*h]; for(int y=0; y<h; y++) for(int x=0; x<w; x++) { if(y==0 || x==0 || y==h-1 || x==w-1) data[i]=img1.getRGB(x, y); else { for(int c=y-1; c<=y+1; c++) for(int r=x-1; r<=x+1; r++) colorArray[x-r+1][y-c+1]=new Color(img1.getRGB(r, c)); int red=0, green=0, blue=0; for(int c=0; c<=2; c++) for(int r=0; r<=2; r++) { red+=SHARP_FILTER[r][c]*colorArray[r][c].getRed(); green+=SHARP_FILTER[r][c]*colorArray[r][c].getGreen(); blue+=SHARP_FILTER[r][c]*colorArray[r][c].getBlue(); } red=(red<0)?0:(red>255?255:red); green=(green<0)?0:(green>255?255:green); blue=(blue<0)?0:(blue>255?255:blue); Color c2=new Color(red, green, blue); data[i]=c2.getRGB(); } i++; } BufferedImage img2= new BufferedImage(w, h, BufferedImage.TYPE_INT_RGB); img2.setRGB(0, 0, w, h, data, 0, w); return img2; } |
A metódus meghívása a fájlkezelést is tartalmazó vezérlőmetódusban például így történhet:
|
|
public static void main(String[] args) { try { BufferedImage imageSource=ImageIO.read( new File("./images/Traditional-Japanese-Garden.jpg")); BufferedImage imageSharpen=sharpenEffect(imageSource); ImageIO.write(imageSharpen, "jpg", new File("./images/Traditional-Japanese-Garden-sharpen.jpg")); } catch(Exception e) { // } } |
Az eredeti és élesített képek összehasonlítása
A bal oldalon az eredeti kép, a jobb oldalon az a mátrixszal élesített kép látható:

A bal oldalon az eredeti kép, a jobb oldalon a b mátrixszal élesített kép látható:

A látvány alapján fontos kiemelni, hogy másképpen is lehet összehasonlítást végezni. Például: színtérkép, színmélység, színösszetevők aránya (hisztogram).
Ötletek továbbfejlesztésre
- Konzolos program átvehetné parancssori paraméterként a szűrőmátrixot, vagy annak nevét, kódját, egyes értékeit.
- Grafikus felületű programban vízszinten
JScrollBar GUI komponens(ek) segítségével paraméterezhető, kigörgethető lehetne a szűrőmátrix szélsőértéke(i).
- A fenti effektek a kép összes pixelét érintik. GUI felületen megoldható az is, hogy ki tudjuk jelölni a kép egy-egy részét, amire alkalmazni szeretnénk az effektek. Ez a kijelölés többféle lehet, például téglalap alakú, szabálytalan, átlátszó, adott vagy adotthoz hasonló árnyalatú színű, vagy valaminek a körvonala.
- Egy mappában lévő összes képre alkalmazható effekt, előnézettel, képfájlonként megerősítéssel, jóváhagyással, csoportos kijelöléssel, szűrővel.
- Szürkeskála effekt megvalósítása és tesztelése az alábbi forráskód-részlettel:
|
|
Color c1=new Color(img1.getRGB(x, y)); int gray=(int) (0.21*c1.getRed()+0.72*c1.getGreen()+0.07*c1.getBlue()); Color c2=new Color(gray, gray, gray); |
- Homályosítás effekt megvalósítás és tesztelése a 4 élszomszéd színeinek átlagolásával, így:
|
|
Color cTop=new Color(img1.getRGB(x, y-1)), cRight=new Color(img1.getRGB(x+1, y)), cBottom=new Color(img1.getRGB(x, y+1)), cLeft=new Color(img1.getRGB(x-1, y)); int r=(cTop.getRed()+cRight.getRed()+ cBottom.getRed()+cLeft.getRed())/4, g=(cTop.getGreen()+cRight.getGreen()+ cBottom.getGreen()+cLeft.getGreen())/4, b=(cTop.getBlue()+cRight.getBlue()+ cBottom.getBlue()+cLeft.getBlue())/4; Color c2=new Color(r, g, b); |
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A Java SE szoftverfejlesztő tanfolyamunkon, a szakmai modul Objektumorientált programozás témakörét követő 29-36. óra Grafikus felhasználói felület alkalmain már tudunk egyszerűbb GUI programot tervezni, kódolni, tesztelni, kiegészítve a 37-44. óra Fájlkezelés alkalmaihoz kötődő példaprogramokkal.
 Kép élesítése effektus működése
Kép élesítése effektus működése Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023 Múzeumok Éjszakája 2023 – SZTAKI, Vasarely Múzeum
Múzeumok Éjszakája 2023 – SZTAKI, Vasarely Múzeum Naprendszer szimuláció – megvalósítás Java nyelven
Naprendszer szimuláció – megvalósítás Java nyelven Naprendszer szimuláció – objektumorientált tervezés
Naprendszer szimuláció – objektumorientált tervezés Naprendszer szimuláció – elméleti háttér
Naprendszer szimuláció – elméleti háttér















 A
A 
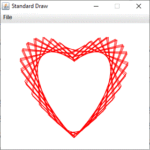 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.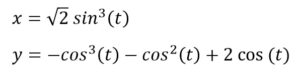



 Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).