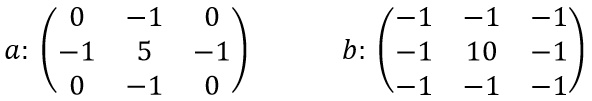Címke: grafikus felhasználói felület
40 blog bejegyzésnél szerepel:
 Kép élesítése effektus működése
Kép élesítése effektus működése
 Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
 Naprendszer szimuláció – megvalósítás Java nyelven
Naprendszer szimuláció – megvalósítás Java nyelven
 Naprendszer szimuláció – objektumorientált tervezés
Naprendszer szimuláció – objektumorientált tervezés
 Naprendszer szimuláció – elméleti háttér
Naprendszer szimuláció – elméleti háttér
 Tankocka – Legyen Ön is milliomos! – Programozás Java nyelven
Tankocka – Legyen Ön is milliomos! – Programozás Java nyelven
 Tankocka – Rövid válasz: Java konstansok
Tankocka – Rövid válasz: Java konstansok
 Tankocka – Párkereső: csomag, osztály, interfész
Tankocka – Párkereső: csomag, osztály, interfész
 Tankocka – Párosítós játék: Programozás Java nyelven
Tankocka – Párosítós játék: Programozás Java nyelven
 Táblázatos komponens testreszabása
Táblázatos komponens testreszabása
 Céline Dion - Courage World Tour
Céline Dion - Courage World Tour
 Dr. Sheldon Cooper szólánc játéka
Dr. Sheldon Cooper szólánc játéka
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017
177 db hozzá kapcsolódó címke:
2017 (24), 2018 (24), 2019 (24), 2020 (24), 2021 (24), 2022 (24), 2023 (24), 2024 (8), adatbázis (25), Agymenők (3), algoritmus (31), állásinterjú (10), álláskeresés (17), animáció (17), AnyChart (1), atipikus megoldás (5), becslés (6), ChatGPT (1), ciklusok (18), csoportmunka (10), csoportváltás (6), dátumkezelés (10), DUF (3), Dunaújvárosi Főiskola (3), élményalapú tanulás (21), előadás műhely-napon (24), elosztott alkalmazás (14), eredménytábla (10), érettségi feladat (8), évforduló (24), fájlkezelés (29), fejtörő (11), Fibonacci (3), fizika (7), fraktál (1), funkcionális programozás (18), gamifikáció (33), GitHub (2), Google Charts (5), Google Cloud Platform (2), grafika (26), hálózatkezelés (14), hatékonyság (28), hierarchikus lekérdezés (7), humor (4), időjárás (2), időzítő (4), IEEE Spectrum (2), Indeed (2), ingyenes esemény (34), ipar 4.0 (6), ipar 5.0 (2), játék (9), Java forráskód (63), JavaFX (3), JavaScript (6), JDBC (12), JExcel API (4), JFreeChart (7), JSON (4), JSP (3), JTable (7), JTree (6), karrier (17), karrierváltás (14), képeffektus (1), keresztrejtvény (2), kígyókocka (2), kivételkezelés (13), kliens-szerver (7), kliensprogram (13), Koch-görbe (1), kockadobás (1), kódolás/dekódolás (6), kollekció (32), kombinatorika (7), konferencia (15), közelítés (3), kriptoaritmetika (2), KSH (3), Kutatók éjszakája (8), lambda kifejezés (13), LEGO (3), lekérdezés (18), lépésszám (9), logikai feladat (21), logisztika (5), lottószelvény (10), matematika érettségi feladat (8), matematika (30), mém (7), memória használat (3), mesterséges intelligencia (12), metódus (30), MMO (6), Multimédia az oktatásban konferencia (6), munkaerőpiac (14), MVC (12), Naprendszer (5), naptár (26), NASA (2), népesedési világnap (1), Neumann János Számítógép-tudományi Társaság (8), NJSZT Multimédia az oktatásban (6), NJSZT (8), nyári tábor (2), okos gyár (5), objektumorientált programozás (85), OpenWeatherMap (2), optikai csalódás (2), Oracle HR séma (12), orientáló modul (39), öröklődés (16), összefoglalás (2), osztálydiagram (7), pályaorientáció (28), pályázat (6), Pi nap (2), Pi (2), ProgCont API (3), programozás (106), programozási tételek (28), projektmunka (5), protokoll (számítógép-hálózat) (3), publikáció (9), PYPL (2), Python (4), rajzolás (15), Reddit (2), rejtjelezés (3), rekurzió (9), rendezvény 2018 (10), rendezvény 2019 (11), rendezvény 2020 (12), rendezvény 2021 (6), rendezvény 2022 (8), rendezvény 2023 (10), RMI (3), robotika (12), robotprogramozás (11), Sankey-diagram (1), soft skill (10), Stack Overflow (2), statisztika (11), STEM (3), Stream API (14), swing (26), szakmai előadás (31), szakmai modul (96), szálkezelés (4), szimuláció (10), sztereogram (1), táblázat (11), tananyagfejlesztés (8), tankocka (15), térinformatika (4), tervezés (41), tesztelés (21), tévésorozat (3), TIOBE (2), tipikus munkanap (6), titkosítás/visszafejtés (4), többféle megoldás összehasonlítása (37), tömb (17), tömegvonzás (5), továbbfejlesztés (23), transzformáció (8), Trendy Skills (2), UML (8), Unity (2), ünnepnap (13), vélemény (4), videó (5), virtuális valóság (5), visszajelzés (5), worldometer (2), XML (8)







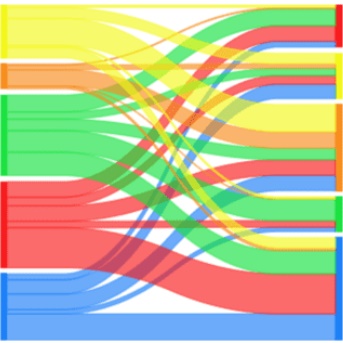








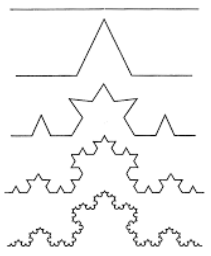



 A
A 
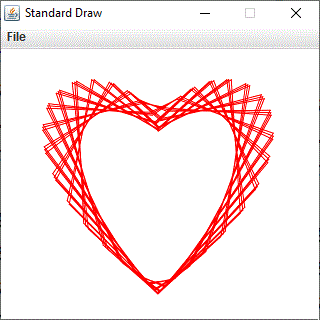
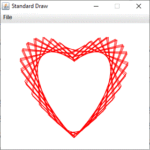 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.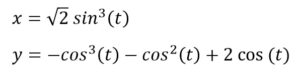



 Időnként készítünk oktatóprogramokat is tanfolyamainkon. Most az volt a cél, hogy kódolás/dekódolás szakterület egyik ismert betűkeveréses algoritmusának működését mutassa be lépésről-lépésre az oktatóprogram. A rácsrejtjelezést választottuk.
Időnként készítünk oktatóprogramokat is tanfolyamainkon. Most az volt a cél, hogy kódolás/dekódolás szakterület egyik ismert betűkeveréses algoritmusának működését mutassa be lépésről-lépésre az oktatóprogram. A rácsrejtjelezést választottuk.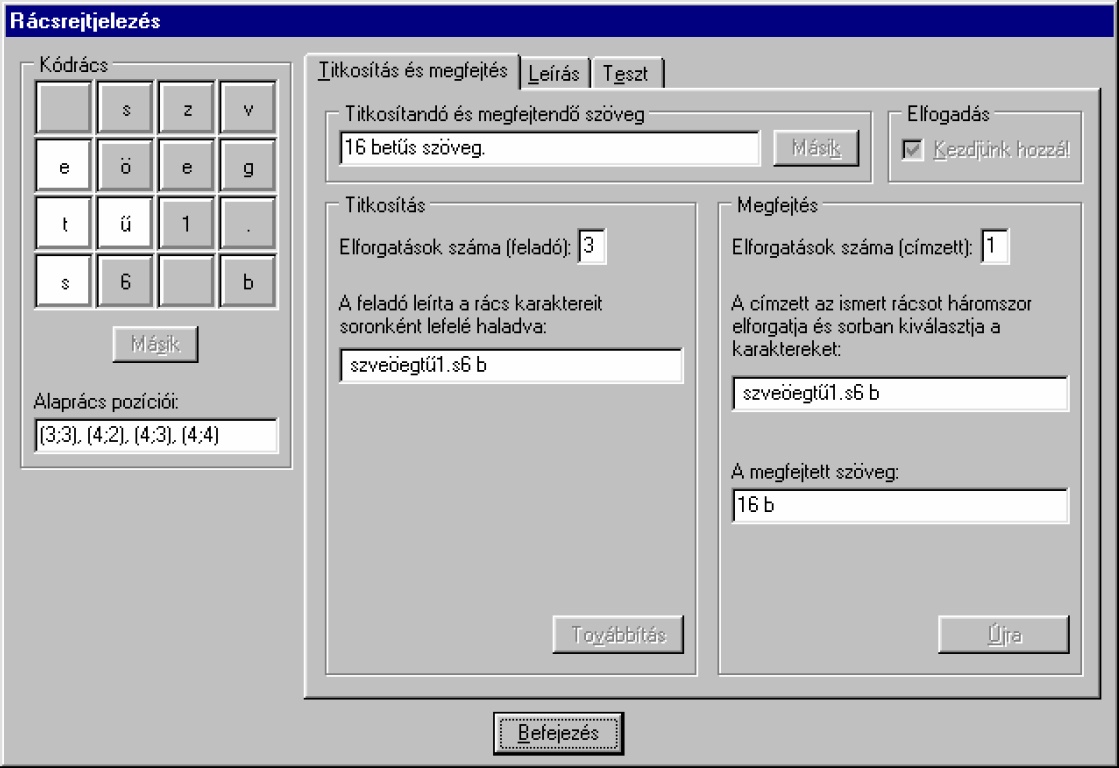
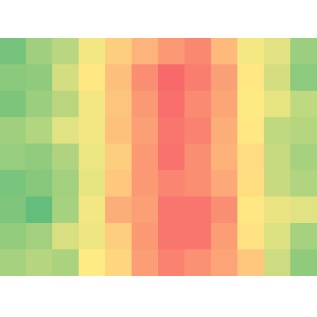
 Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).