Hóesés szimulációt tervezünk és valósítunk meg Java nyelven. A téma igazi örökzöld. Elvileg minden télen aktuális. 😉 A grafikus felülethez és az eseménykezeléshez a swing gyűjteményt használjuk. Adott egy téglalap alakú terület amelyen – méretéhez igazodva – több száz hópehely mocorog. A területet önállóan programoztuk le – azaz ez alkotja a teljes GUI-t –, de lehetne egy nagyobb kép része is. Többféleképpen is beépítünk véletlenszerűséget a szimulációba. Tervezünk is, hiszen az sosem árt. 😉
Többnyire beépített komponenseket, elemeket használunk, de van saját, örökítéssel testre szabott komponensünk is:
- A szimuláció a Window osztályból példányosított felületen működik, amely JFrame utód. Nem átméretezhető és látható.
- A területet JPanel típusú pnTransparentWindow alkotja. Mérete 300*200 pixel. Színe a szürke egyik árnyalata. Ezen mozognak a hópelyhek.
- A hópehely Snowflake típusú JPanel utód. Mérete 2*2 pixel. Színe fehér. Saját swing-es Timer biztosítja az eseménykezelését. A szimulációban 600 hópehely szerepel.
Az elkészült szimuláció
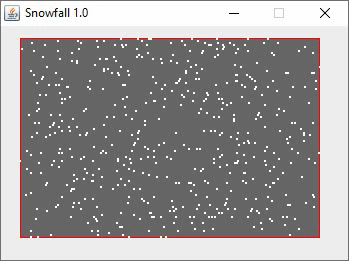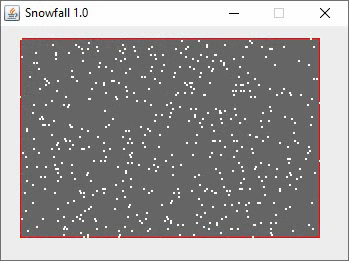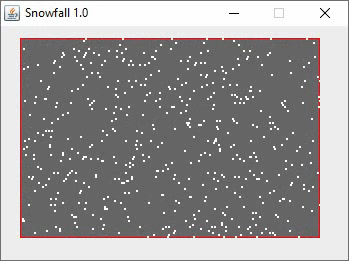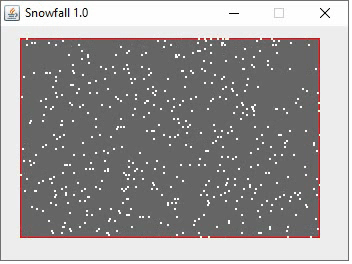
A teljes forráskódból íme a hópehely megvalósítása
|
1 2 3 4 5 6 7 |
public class Snowflake extends JPanel { private Rectangle rectangle=null; private Dimension size=new Dimension(2, 2); private int delay=(int)(Math.random()*5+1)*50 private Timer timer=new Timer(delay, (ActionEvent e) -> { move(); }); |
A hópehelynek „tudnia kell” hol van, azaz mekkora területen mozoghat, ez a rectangle. A hópehelynek van size mérete. A hópehely saját magát mozgatja a területen a timer segítségével. Az időzítés várakoztatására/késleltetésére vonatkozó delay értéke véletlenszerűen 50, 100, …, 250 milliszekundum lehet. Másképpen: a szél által össze-vissza fújt hópelyhek között lehetnek lassabban és gyorsabban mozgók is. Az eseményobjektumhoz lambda kifejezés rendeli hozzá a reakciót jelentő, mozgást megvalósító move() metódus meghívását, amely így adott időközönként bekövetkezik.
|
1 2 3 4 5 6 7 8 9 10 |
public Snowflake(JPanel pnTransparentWindow) { rectangle=pnTransparentWindow.getBounds(); setPreferredSize(size); int x=(int)(Math.random()*rectangle.width); int y=(int)(Math.random()*rectangle.height); setBounds(x, y, size.width, size.height); setOpaque(true); setBackground(Color.WHITE); timer.start(); } |
A hópelyhet a konstruktora hozza létre. Átveszi azt a pnTransparentWindow területet, amelyre később rákerül a Window példányosítása során. A gyengébb setSize() metódus helyett az erősebb setPreferredSize() metódus állítja be a méretet. Véletlenszerű x és y pozícióba kerül ki/fel a területre. A setBounds() örökölt metódus beállítja a pozícióját és méretét. Erre épít a fogadó oldalon az abszolút helyzet, külön elrendezésmenedzser nélkül. Végül a hópehely átlátszó, fehér és elindítja saját időzítőjét a timer.start() metódushívással.
Az időzítés/várakoztatás véletlenszerűsége után íme a második véletlenszerűség a szimulációban. A hópehely mozgása során a szél által össze-vissza fújva eltérő eséllyel/valószínűséggel mozog 8 lehetséges irányba az alábbiak szerint:
- 5-5% eséllyel felfelé, azon belül jobbra vagy balra (átlósan),
- 10-10% eséllyel jobbra vagy balra,
- 20-20% eséllyel lefelé, azon belül jobbra vagy balra (átlósan),
- 30% eséllyel lefelé, függőlegesen,
- felfelé, függőlegesen nem mozog.
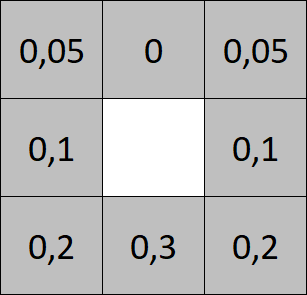
Az esélyek összege 100%. Másképpen kulcsszavakban: 1 = biztos esemény (teljes eseménytér, nincs más lehetőség), egymást kizáró események, geometriai valószínűség. A képen középen lévő hópehely a 8 szomszédja közül a 7 szóba jöhető közül valamelyikre adott eséllyel mozog. A geometriai valószínűséget az ábra alapján az óramutató járásával megegyezően leképeztük az 1..100 intervallumra:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
public void move() { Point location=getLocation(); int tip=(int)(Math.random()*100+1); //1-100 if(1<=tip && tip<=5) location.translate(size.width, -size.height); //jobbra fel else if(6<=tip && tip<=15) location.translate(size.width, 0); //jobbra else if(16<=tip && tip<=35) location.translate(size.width, size.height); //jobbra le else if(36<=tip && tip<=65) location.translate(0, size.height); //le else if(66<=tip && tip<=85) location.translate(-size.width, size.height); //balra le else if(86<=tip && tip<=95) location.translate(-size.width, 0); //balra else //96<=tip && tip<=100 location.translate(-size.width, -size.height); //balra fel if(rectangle.height<location.y) location.translate(0, -(int)location.getY()); setLocation(location); } |
A move() metódus megvalósítja a fenti tervnek megfelelően a hópehely mozgatását. Első lépésben tudni kell a jelenlegi/kiinduló location helyét (a bal felső csúcs, elkérjük). Ezután véletlenszerű esély/ tip generálódik. Az első elágazásban a hópehely translate() metódusával eltoljuk az előbb elkért pontot. Az eltolás relatív. Az utolsó elágazásban kompenzálunk, ha a hópehely alul kilépne a területről. Ekkor felül újra belép a területre. Végül beállítjuk a hópelyhet megvalósító komponenst a manipulált location helyre.
Takarékosak vagyunk: ezzel a megoldással „újrahasznosítjuk” a hópelyheket. Csak annyi van belőlük, amennyi szükséges. Nem kell őket folyamatosan megszüntetni és újra létrehozni. Nem mozognak feleslegesen. Nem mozognak olyan területen, ahol nem láthatóak.
Ötletek továbbfejlesztésre
- A hópelyhek színe lehetne véletlenszerű a fehér és a középszürke között. Ezzel a nézőtől való távolságot, esetleg a kép élességét lehetne modellezni.
- A szél nem feltétlenül szimmetrikus, vagy a hópelyhek mozgatását meg lehetne oldani jobbra és balra eltérő eséllyel is.
- A terület lehetne más alakú, például trapéz, íves, kör, ellipszis.
- Másképpen is vezérelhetnénk a szimulációt. Ahelyett, hogy most minden hópehelynek van saját időzítője, lehetne csak 5 db (lassabbak és gyorsabbak), amelyek közül véletlenszerűen kiválaszthatnánk, hogy melyik hatására mozgatjuk az adott hópelyhet. Fordítva is mehetne: az 5 db időzítőhöz előre hozzárendelhetnénk a hópelyheket. Ez így más-más felelősség, kommunikáció, üzenetküldés, vezérlés lenne az objektumok között. Hasznos tapasztalat lehet megvalósítani bármelyiket.
- A terület lehetne egy nagyobb kép része. Például meghatározhatnánk egy tetszőleges átlátszóságot (színt vagy arányt) és többrétegű felületet megvalósítani képes JLayeredPane komponens elé vagy mögé is elhelyezhető lehetne a terület a grafikus felületen.
- Aki kihívást keres: illessze a területet az alábbi hangulatos képre úgy, hogy a középső ablakok téglalap alakúak, a két szélső trapéz alakú vagy perspektivikus nézetű és a kör/ellipszis alakú tükörben pedig tükröződik valahonnan a hóesés látványa.
- Még bátrabbaknak: a kandallóban lévő tüzet is lehet hasonlóan szimulálni. Itt már többféle fizikai paraméter is figyelembe vehető, például fényerősség, tükröződés. Egy 3D modellezett térben a sugárkövetés (Ray Tracing) algoritmus is megvalósítható. A hópelyheknél lehetne az egyszerű mozgástól eltérő más fizikát is programozni: rugalmas ütközéssel összetapadhatnának vagy rugalmatlan ütközéssel lepattanhatnának egymásról és mindez hathatna a sebességükre is.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A Java SE szoftverfejlesztő tanfolyamunkon, a szakmai modul Objektumorientált programozás témakörét követő 29-36. óra Grafikus felhasználói felület alkalmain már tudunk egyszerűbb szimulációs programot tervezni, kódolni, tesztelni.
Aki haladó már az GUI animáció területén, annak ajánlom a Denevérek a barlangban esettanulmányunkat. Látványban hasonló, de architekturálisan jóval összetettebb és hálózati kommunikációt is használ.
Egyszerű ötlet a továbbfejlesztésre: az utolsó forráskód 19. sorának módosításával könnyen elérhető, hogy az újrahasznosított hópehely ne olyan kiszámítható módon ott jöjjön vissza felül, ahol alul kiment (jobbra-balra értem) az x koordinátát. A 0 helyett legyen
(int)(Math.random()*rectangle.width), ahogyan kezdetben is.Köszi András. Jó ötlet és működik is, bár olyan sokan vannak a hópelyhek, hogy nem nagyon lehetne észrevenni ezt a változást.
Kipróbáltam a
JLayeredPane-t a pingvines/füles mintapéldával. Megmutatom majd a hétvégi órán.Kíváncsian várjuk Anikó! 😉
Aki még nem ismeri, Anikó erre gondolt: How to Use Layered Panes