 Ebben a projektben táblázatos hőtérképet készítünk Java és JS nyelveken. Java programot készítünk az adatok véletlenszerű előállításához és a sablon alapján történő HTML fájl generálásához. JavaScript program fogja a grafikont megjeleníteni a weboldalon. Tervezünk, kódolunk, tesztelünk. Lássunk hozzá!
Ebben a projektben táblázatos hőtérképet készítünk Java és JS nyelveken. Java programot készítünk az adatok véletlenszerű előállításához és a sablon alapján történő HTML fájl generálásához. JavaScript program fogja a grafikont megjeleníteni a weboldalon. Tervezünk, kódolunk, tesztelünk. Lássunk hozzá!
Mi az a hőtérkép?
A hőtérkép (heatmap) olyan grafikon, amely könnyen áttekinthetővé tesz nagy mennyiségű adatot úgy, hogy kategorizál/csoportosít és az előfordulások tartományai alapján különböző színeket rendel azokhoz. A szín hozzárendelése egy intervallumból történik. Például a világosabb a ritkább, a sötétedő szín az egyre gyakoribb értékeket jelenti. A tipikus hőtérkép kétdimenziós és az előforduló adatok mennyiségét, azok arányait, eloszlását, szóródását (nem szórását), gyakoriságát jeleníti meg. A hőtérkép gyors vizuális összefoglalást, áttekintést biztosít. A projekt során sorokból és oszlopokból álló táblázatos hőtérképet készítünk.
A táblázatos hőtérkép nem összekeverendő a következő két megközelítéssel:
- Ha az adatok lokációhoz kötődnek és térképen jelennek meg, akkor azt tematikus térképnek nevezzük. Erről már blogoltam korábban, lásd: Céline Dion – Courage World Tour, amikor az énekesnő USA-beli államokban előforduló koncertjeinek számát jelenítettem meg. Ehhez hasonlók az amerikai elnökválasztás során használt tematikus térképek, amelyek a(z egyes) jelöltek szavazatainak arányát ábrázolják meg szintén államonként.
- Ha az adatok webergonómiához, bannervaksághoz, inkább fókuszban lévő tartalmakhoz, felhasználói élmény (UX) tervezéshez kötődnek, akkor a weboldal grafikus elemeihez (azok pozíciója) alapján rendelünk hozzá színeket attól függően, hogy mennyi ideig nézi azt a felhasználó.
Mi a feladat (koncepcionálisan)?
Adott egy konditerem, amely hétköznapokon egy megadott időintervallumban használható. Ehhez kulcsot kell felvenni és leadni. Az első belépő nyitja és az utolsó távozó zárja az ajtót. A teremhasználat offline nyilvántartott, így nehézkes bármiféle kimutatás, statisztika. A „menet közbeni” jövés-menést nem tudjuk követni. Természetesen adott számos szabály (felelősség, biztonság, balesetvédelem, létszámkorlát), amit most nem részletezek.
Elhelyezünk az ajtó mellett, belülről egy belépéshez és egy távozáshoz tartozó QR kódot. Készítünk egy egyszerű mobil alkalmazást és megkérjük a konditermek használóit, hogy belépéskor és távozáskor „csekkoljanak”. Anonim gyűjtjük a belépések és távozások időpontját (valahol egy szerveren, bármilyen fájlban, adatbázisban).
A konditermek használatára vonatkozó összesített adatokat könnyen átlátható módon szeretnénk weboldalon megjeleníteni: heti bontásban, a nyitva tartás időszakát órás blokkokra bontva az igénybevételtől függően jelenjenek meg az adatok táblázatos hőtérképen.
Ez az állapot átmeneti. Segítheti a konditermekbe tervezett – egyéni használattól független – események ütemezését. Ezeket akkor lenne célszerű időzíteni, amikor nem, alig, vagy kevésbé használt, foglalt az adott konditerem. A továbbfejlesztés következő állapotában könnyen lecserélhető a QR kód RFID alapú proximity kártyára, proxy kulcstartóra: először csak a jelenlét nyilvántartásához, később akár az ajtó nyitásához is.
Mit valósítunk meg mindebből Java nyelven?
Egyetlen konditeremre fókuszálunk. A hétköznaponként nyitva tartás legyen 16 órától 21 óráig. Aki edzésre jön, véletlenszerűen 20 és 40 perc közötti időszakot tölt a konditeremben. 16 órától lehet belépni. Az utolsó belépés 20:40-kor lehet (érdemes). 21 órakor mindenki elhagyja a konditermet. Nem fordul elő, hogy valaki nem jelzi a belépését vagy a távozását. Mivel anonim a nyilvántartás, így elegendő a dátum/időhöz, időbélyeghez egyetlen állapotot tárolni: be vagy ki. Valaki belépett nyitáskor vagy valamikor utána, majd távozott 20-40 perccel később, de legfeljebb záráskor.
A szükséges adatokat véletlenszerűen állítjuk elő. Egy hétre vonatkozó adatokat generálunk. Ezek a fenti paramétereknek megfelelő, összetartozó belépéshez és távozáshoz köthető időpontok. Kiegészítve a napok ciklusban való léptetésével hétfőtől péntekig. Az adatokat feldolgozva, összegyűjtve, csoportosítva, kategorizálva olyan (kimeneti) formátumra alakítjuk, amely kompatibilis a táblázatos hőtérkép adatmodelljével (bemenetével). Mindez Java nyelven valósul meg.
Mi történik JavaScript nyelven?
A webes megjelenítéshez szükséges egy HTML fájl, amelyben beágyazva található meg egy téglalap alakú területként megjelenő táblázatos hőtérkép. Ez sokféleképpen testre szabható: adható hozzá felirat, beállítható a sorokhoz és oszlopokhoz tartozó szöveg és a táblázat celláiban megjelenő értékek, adott a lebegő, az egér kurzor helyzetétől függő – cellánként különböző – jelmagyarázat, és persze mindennek van formátuma (betűtípus, méret, szín, igazítás, kitöltés). A fix, adatoktól nem függő beállításokat tartalmazó weboldalt sablonként elkészítjük. Mindez JavaScript nyelven történik. Ezután Java program a weboldal sablonját kiegészíti (cseréli, behelyettesíti, feltölti) a szükséges adatokkal.
Hogyan alakul az időintervallumok átfedése?
A konditerem használatának alakulását követjük, amihez táblázatos hőtérképet készítünk. Ehhez a nyitva tartás időintervallumát órás blokkokra bontjuk. Blokkonként összesítjük a jelenlétet, azaz megszámoljuk, hogy éppen akkor hányan veszik igénybe a konditermet, hányan vannak jelen/benn.
A konkrét paraméterektől függően az alábbi képen látható 3 eset egyike fordulhat elő. A és B jelöli az órás blokk elejét és végén, tehát ez 60 perces intervallum. Tarthat például: 16:00:00-16:59:59-ig. X és Y jelöli a jelenlét intervallumát, azaz a belépés és távozás időpontjait. Ez 20 és 40 perc között alakul. Haladjunk balról jobbra az ábrán.
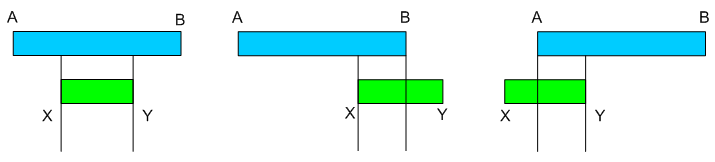
Az első esetben ugyanarra az órára esik a belépés és a távozás. Ez az eset egyértelmű. A másik két esetben átfedés van több órás blokk között, mert különböző órára esik a belépés és a távozás. El kell dönteni, hogy ekkor hogyan összesítjük a jelenlétet. Válasszunk az alábbi két módszer közül:
- Az első módszer szerint mindkét órához – ahol átfedés van – összesítjük a jelenlétet 1-1 főként, hiszen ha nem is végig, de jelen volt mindkét órás blokkban. Például: egy 16:50:00-17:20:00 jelenlétet a 16 és 17 órás blokkban is figyelembe veszünk.
- A második módszer szerint időarányosan tesszük mindezt, azaz súlyozunk aszerint, hogy milyen hosszú jelenlét esik az egymást követő órákban. Például: egy 16:50:00-17:20:00 jelenlétet a 16 órás blokk esetében egyharmad, a 17 órás blokk esetében kétharmad a jelenlét adott órára eső aránya, súlya.
Az első módszert valósítjuk meg. Ez a döntés jelentősen befolyásolja, hogyan kell értelmezni később az elkészült táblázatos hőtérképet.
Objektumorientált tervezés
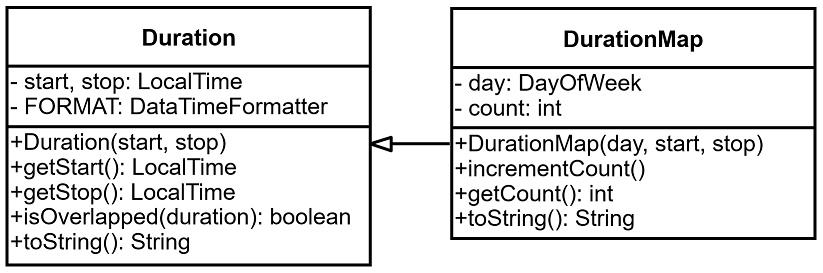
A koncepcionális terv alapján modellezünk. A szükséges adatok tárolására és alapfunkcióira fókuszálunk. Az osztály tárolja az összetartozó adatokat és megvalósít rajtuk értelmezhető műveleteket. Az időintervallum/időtartam kezelését a
Duration ősosztály oldja meg. Tárolja a
start és
stop – naptól független időpontokat tároló – adatok és a rájuk vonatkozó
FORMAT – megjelenítéshez kötődő – konstanst. Biztosítja a szükséges műveleteket: konstruktor, getterek, megvalósítja az időintervallumok átfedését az
isOverlapped() függvénnyel, valamint ad szöveges reprezentációt a
toString() függvénnyel. Az ősosztályból öröklődik az utódosztály. A
DurationMap osztály a naptól független időpontokat kibővíti a hozzájuk tartozó
day nappal, valamint képes tárolni az összesített, megszámolt jelenlétet a
count változóban. Részt vesz a megszámolás folyamatában azzal, hogy lépésenként meghívható az
incrementCount() eljárása.
 A
java.time csomagbeli
LocalTime osztály képes a dátumtól független, napon belüli időpont tárolására és biztosít néhány alapvető funkciót a kezelésükre. Az adattárolás a napon belül eltelt időn alapul és nekünk (bőven) elegendő a másodperc alapú megjelenítés. A
DateTimeFormatter alkalmas ezen időpontok formátumának tárolására, például
óó:pp:mm alakban.
A
java.time csomagbeli
LocalTime osztály képes a dátumtól független, napon belüli időpont tárolására és biztosít néhány alapvető funkciót a kezelésükre. Az adattárolás a napon belül eltelt időn alapul és nekünk (bőven) elegendő a másodperc alapú megjelenítés. A
DateTimeFormatter alkalmas ezen időpontok formátumának tárolására, például
óó:pp:mm alakban.
A
Duration osztályból annyi objektum készül, ahány jelenlét adódik véletlenszerűen. Akár több száz is lehet. A
DurationMap osztályból generált objektumok száma jóval kevesebb. Heti 5 napra, napi 5 órás blokkra 25 db készül belőle.
A vezérléshez kötődő osztály tervezését nem részletezem.
Íme a Java forráskód
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
public class Heatmap { private final DayOfWeek[] WORKDAYS=new DayOfWeek[] { DayOfWeek.MONDAY, DayOfWeek.TUESDAY, DayOfWeek.WEDNESDAY, DayOfWeek.THURSDAY, DayOfWeek.FRIDAY}; private final LocalTime ENTER_START_TIME=LocalTime.of(16, 0, 0); private final LocalTime ENTER_STOP_TIME=LocalTime.of(20, 40, 0); private final LocalTime EXIT_TIME=LocalTime.of(20, 59, 59); private final DateTimeFormatter FORMAT= DateTimeFormatter.ISO_LOCAL_TIME; private final Path HEATMAP_TEMPLATE_FILE= Paths.get("./files/heatmap-template.html"); private final Path HEATMAP_FILE=Paths.get("./files/heatmap.html"); private ArrayList<DurationMap> durationMapAllList=new ArrayList<>(); public Heatmap() { overlapTest(); createHeatmapFile(); } private void overlapTest() { for(DayOfWeek day: WORKDAYS) { LocalTime intervalStart=ENTER_START_TIME; LocalTime intervalStop= intervalStart.plusHours(1).minusSeconds(1); ArrayList<DurationMap> durationMapDayList=new ArrayList<>(); for(int i=1; i<=5; i++) { DurationMap interval= new DurationMap(day, intervalStart, intervalStop); durationMapDayList.add(interval); intervalStart=intervalStart.plusHours(1); intervalStop=intervalStop.plusHours(1); } ArrayList<Duration> durationList=new ArrayList<>(); for(int i=1; i<=10; i++) { int startSec=ENTER_START_TIME.toSecondOfDay(), stopSec=ENTER_STOP_TIME.toSecondOfDay(); int randomSec= (int)(Math.random()*(stopSec-startSec+1)+startSec); LocalTime startTime=LocalTime.ofSecondOfDay(randomSec); int presenceMin=(int)(Math.random()*21+20); LocalTime stopTime=LocalTime.ofSecondOfDay(Math.min( startTime.toSecondOfDay()+presenceMin*60, EXIT_TIME.toSecondOfDay())); durationList.add(new Duration(startTime, stopTime)); } durationMapDayList.stream().forEach((durationMap) -> { durationList.stream(). filter((duration) -> (duration.isOverlapped(durationMap))). forEach((duration) -> { durationMap.incrementCount(); }); }); durationMapAllList.addAll(durationMapDayList); } } private void createHeatmapFile() { String heatmapData=durationMapAllList.stream(). map(DurationMap::toString).collect(Collectors.joining(",\n")); try { String html=Files.readAllLines(HEATMAP_TEMPLATE_FILE).stream(). collect(Collectors.joining("\n")); html=html.replace("##HEATMAP_DATA##", heatmapData); Files.write(HEATMAP_FILE, html.getBytes(), StandardOpenOption.CREATE); } catch(IOException e) { e.printStackTrace(); } } public static void main(String[] args) { new Heatmap(); } } |
A Java forráskód minden megtervezett funkciót megvalósít, támogatva a koncepciót. Most nem részletezem a működését.
A véletlenszerűen előállított adatok
A lista görgethető:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
{x: "hétfő", y: "16:00:00-16:59:59", heat: 4}, {x: "hétfő", y: "17:00:00-17:59:59", heat: 6}, {x: "hétfő", y: "18:00:00-18:59:59", heat: 9}, {x: "hétfő", y: "19:00:00-19:59:59", heat: 6}, {x: "hétfő", y: "20:00:00-20:59:59", heat: 6}, {x: "kedd", y: "16:00:00-16:59:59", heat: 6}, {x: "kedd", y: "17:00:00-17:59:59", heat: 10}, {x: "kedd", y: "18:00:00-18:59:59", heat: 6}, {x: "kedd", y: "19:00:00-19:59:59", heat: 7}, {x: "kedd", y: "20:00:00-20:59:59", heat: 3}, {x: "szerda", y: "16:00:00-16:59:59", heat: 5}, {x: "szerda", y: "17:00:00-17:59:59", heat: 9}, {x: "szerda", y: "18:00:00-18:59:59", heat: 5}, {x: "szerda", y: "19:00:00-19:59:59", heat: 7}, {x: "szerda", y: "20:00:00-20:59:59", heat: 7}, {x: "csütörtök", y: "16:00:00-16:59:59", heat: 4}, {x: "csütörtök", y: "17:00:00-17:59:59", heat: 6}, {x: "csütörtök", y: "18:00:00-18:59:59", heat: 11}, {x: "csütörtök", y: "19:00:00-19:59:59", heat: 7}, {x: "csütörtök", y: "20:00:00-20:59:59", heat: 5}, {x: "péntek", y: "16:00:00-16:59:59", heat: 4}, {x: "péntek", y: "17:00:00-17:59:59", heat: 8}, {x: "péntek", y: "18:00:00-18:59:59", heat: 4}, {x: "péntek", y: "19:00:00-19:59:59", heat: 7}, {x: "péntek", y: "20:00:00-20:59:59", heat: 4} |
A weboldal sablonja
HTML és JavaScript nyelvű forráskód vegyesen. A Java program a fájl 31. sorában lévő
##HEATMAP_DATA## szöveget cseréli le a táblázatos hőtérkép megjelenítéséhez szükséges véletlenszerűen előállított adatokra.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
<html> <head> <title>Heatmap in JavaScript</title> <script src="https://cdn.anychart.com/releases/8.11.0/js/anychart-core.min.js"></script> <script src="https://cdn.anychart.com/releases/8.11.0/js/anychart-heatmap.min.js"></script> <style type="text/css"> html, body, #container { width: 80%; height: 80%; margin: 20pt; padding: 20pt; } </style> </head> <body> <div id="container"></div> <script> anychart.onDocumentReady(function () { let chart=anychart.heatMap(getData()); chart.title("Hogyan alakul a konditerem látogatottsága?"); chart.tooltip().useHtml(true).titleFormat(function () { return "Látogatottság: "+this.heat; }).format(function () { return ( '<span style="color: #CECECE">Nap: </span>'+this.x+"<br/>"+ '<span style="color: #CECECE">Időtartam: </span>'+this.y ); }); chart.container("container"); chart.draw(); }); function getData() { return [ ##HEATMAP_DATA## ]; } </script> </body> </html> |
További részletekért, beállításra vonatkozó, testre szabási lehetőségekért érdemes tanulmányozni az AnyChart dokumentáció Heat Map Chart fejezetét.
Az eredmény
Az előállított weboldalt böngészőben megjelenítve ezt kaphatjuk eredményként (vagy a véletlenszerűen generált adatoktól függően hasonlót):
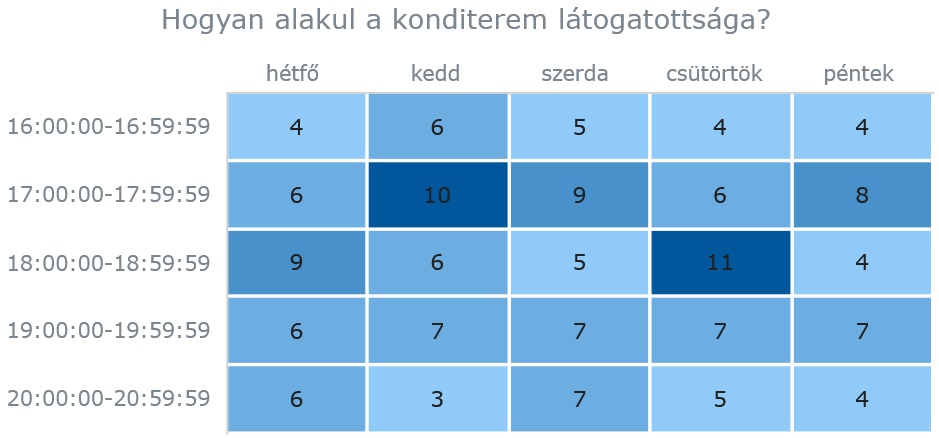
A táblázatos hőtérkép hasznos eszköz. Elemezve könnyen döntéseket hozhatunk a koncepcionális tervezés során vázoltak alapján.
Továbbfejlesztési lehetőségek
- Lehetne több konditerem is. Ekkor rögtön felmerül az összehasonlítás lehetősége, egyben igénye is.
- Lehetne hétköznaponként eltérő a konditerem nyitva tartása.
- Az időpontok kezelési precíz. Egy másodpercen múlik, hogy nem fedik át egymást. Az időpontok megjelenítése lehetne
óó:pp alapú is.
- Az időintervallumok jelenleg állandóak, mindig 1 órásak. Könnyen megoldható lenne, hogy dinamikusak legyenek: például a népszerűbb időszakok felbonthatók lennének két 30 perces blokkra. A népszerűség értelmezhető minden nap (héten) másképp. Egyszerű képlettel: átlag felett, medián felett.
- Általánosíthatnánk a létesítménygazdálkodáshoz kötődő erőforrást nem (feltétlenül) helyhez kötött, mozgatható, kölcsönözhető eszközökre is: hangszer, projektor, stúdió felszerelés.
- Másképpen valósulna meg az adatgyűjtés, ha egyetlen QR kód állna rendelkezésre és back-end helyett a „mobil alkalmazás emlékezne” a belépésre és távozásra. Ez jelentheti legalább az aznapi adatokat, de tárolható historikusan is.
- Hibát is kellene, lehetne kezelni. Például a kiléptetés lehetne automatikus a nyitva tartás végén. A jelenlét igazából igaz-hamis állapot: ha eddig hamis volt és történt valami, akkor igaz lesz és fordítva. Ha van mögötte állapotmegőrző emlékezet (mivel programozunk, így nyilvánvalóan azonnal objektumra gondolunk, vagy annak valamilyen fájlba vagy adatbázisba történő leképezésére).
- A nyilvántartás könnyen megvalósítható személy hozzárendelésével, azaz lehetne nem anonim is a jelenlét.
- Egymást átfedő időpontok esetén (ha nincsenek a hosszukra vonatkozó korlátozó feltételek) általánosítva 6 eset fordulhat elő. Például ha a jelenlét lehetne 60 percnél hosszabb, de 120 percnél rövidebb is, akkor nem lenne elegendő a fenti 3 esetet kezelni a jelenlét összesítése során.
- Valósítsuk meg az időintervallumok átfedésénél bemutatott második – időarányos – módszert!
- A napi jelenlét 20 fővel valósul meg a programban. Lehetne ez a paraméter is véletlenszerű, például 15-30 fő között, vagy esetleg népszerűbb a péntek.
- Jelenleg a táblázatos hőtérkép statikus. Csak a (befejezett egész heti) múltbeli adatokat tudja megjeleníteni. Az aktuális, jelenlegi állapothoz szinkronizáció, ütemezés kell. Óránként (a blokkok végén automatizáltan), de akár 5 percenként is aktualizálható a hőtérkép.
- A táblázatos hőtérkép megjelenítése önálló weboldal helyett beágyazható widget felületén is történhet.
- Többféleképpen is készítettünk már grafikonokat, íme néhány a szakmai blogunkból: Kockadobás kliens-szerver alkalmazás, Sankey-diagram készítése, JFreeChart grafikon készítése.
A bejegyzéshez tartozó forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A projektfeladat – attól függően, milyen szinten valósítjuk meg – kapcsolódhat több tanfolyamunk tematikájához. A fenti forráskód a Java SE szoftverfejlesztő tanfolyam 17-28. óra: Objektumorientált programozás és a 37-44. óra Fájlkezelés alkalmaihoz kötődik. Ha többrétegű, elosztott alkalmazásként valósítjuk meg, akkor a Java EE szoftverfejlesztő tanfolyam a 9-16. óra: XML és JSON feldolgozás, dinamikusan generált weboldalba beépítve a 33-40. óra: Java Server Pages alkalmaihoz kapcsolódik. Ha fájlok helyett egyszerű adatbázist használnánk, akkor a Java SE szoftverfejlesztő tanfolyam 45-52. óra: Adatbázis-kezelés JDBC alapon, ha objektumrelációs leképezéssel oldanánk meg, akkor a Java EE szoftverfejlesztő tanfolyam 25-32. óra: Adatbázis-kezelés JPA alapon alkalmakhoz kötődhet.
 Kép élesítése effektus működése
Kép élesítése effektus működése Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023 Alkalmazottak életpálya modellje – mi lenne, ha…?
Alkalmazottak életpálya modellje – mi lenne, ha…? Naprendszer szimuláció – megvalósítás Java nyelven
Naprendszer szimuláció – megvalósítás Java nyelven Naprendszer szimuláció – objektumorientált tervezés
Naprendszer szimuláció – objektumorientált tervezés Naprendszer szimuláció – elméleti háttér
Naprendszer szimuláció – elméleti háttér Egy matematika érettségi feladat megoldása programozással 2022
Egy matematika érettségi feladat megoldása programozással 2022 Programozás Java nyelven könyv - új, 2022-es kiadás
Programozás Java nyelven könyv - új, 2022-es kiadás


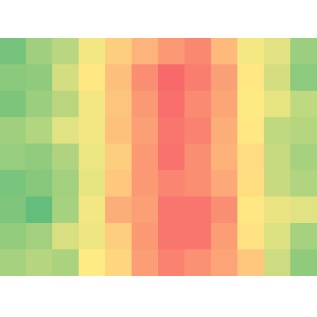











 A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
A PDF népszerű fájlformátum. Az Adobe cég 30+ éves szabványa. Hordozható: azaz minden eszközön, platformon ugyanúgy jelenik meg. Számos nézegető program támogatja, köztük böngészőprogramok is. A PDF rövidítés a Portable Document Format betűszava. Többnyire kimeneti formátumnak tekinthető. Az évek során folyamatosan fejlődött: ma már űrlapokat is tartalmazhat, elektronikusan aláírható, hitelesíthető, és hivatalos ügyek során is használják.
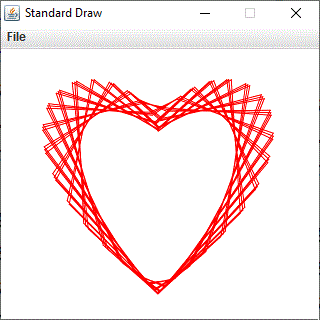
 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.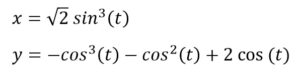



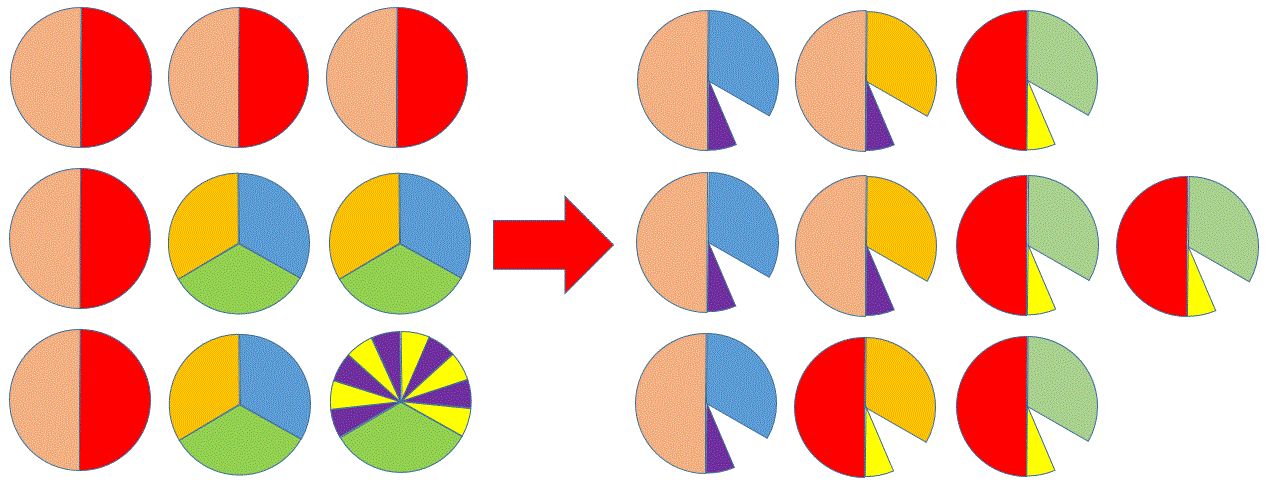
 Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).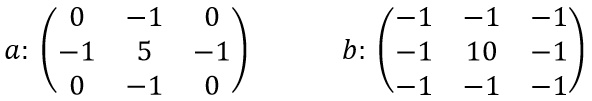


 Ebben a projektben táblázatos hőtérképet készítünk Java és JS nyelveken. Java programot készítünk az adatok véletlenszerű előállításához és a sablon alapján történő HTML fájl generálásához. JavaScript program fogja a grafikont megjeleníteni a weboldalon. Tervezünk, kódolunk, tesztelünk. Lássunk hozzá!
Ebben a projektben táblázatos hőtérképet készítünk Java és JS nyelveken. Java programot készítünk az adatok véletlenszerű előállításához és a sablon alapján történő HTML fájl generálásához. JavaScript program fogja a grafikont megjeleníteni a weboldalon. Tervezünk, kódolunk, tesztelünk. Lássunk hozzá!
 A
A
