A kígyókocka (snake cube, chain cube) 27 egyforma méretű, egymáshoz képest mozgatható/forgatható kockából áll. A kockákat összeköti egy rugalmas fonal/gumi. Az első és az utolsó kocka egy-egy lapján egy-egy lyuk van. A közbenső kockák hat lapjából kettő lyukas. Fából és műanyagból is készülhetnek. Általában kétféle színnel színezettek a kockák. A cél, hogy a 27 kockát kígyózva „összehajtogatva” a kígyó (lánc) összeálljon egy nagyobb 3x3x3 méretű kockává.
Ez egy két részből álló blog bejegyzés 1. része. A blog bejegyzés 2. része itt található.
A színek – a játék gyártóitól függően – nehézségi szinteket jelölhetnek (zöld, kék, piros, narancs, lila). Léteznek könnyebben és nehezebben megoldható kígyókockák. Előbbieknél többször fordul elő két egymással szemben lévő lyukas lap a közbenső kockákon, utóbbiaknál gyakoribbak az egymással szomszédos lapokon lévő lyukak. Másképpen: előbbiben több a három hosszú egyenes rész, utóbbi szinte állandóan tekereg. Általában a kocka egyik csúcsából kezdjük a megoldást, de az igazán nehéz játékok esetében a kígyó indulhat akár a kocka egyik lapjának (3×3) középső kockájától is.
Vannak olyan kígyókockák, amelyeknek több megoldása is van, azaz többféleképpen is összeállítható kockává. Ezek részletes ismertetése (típusok, gyártók, színek), a megoldások (statikusan és dinamikusan), irányokat mutató jelölésrendszer (Front, Left, Up, Back, Right, Down) elérhető Jaap Scherphuis – holland puzzle rajongó – weboldalán: Jaap’s Puzzle Page.
Olyan Java programot készítünk, amely véletlenszerű kígyókockát állít elő.
Tervezés
Szükséges egy háromdimenziós tömb adatszerkezet a kocka tárolására. Több okból is hasznos, ha a tömb mérete 5x5x5. Egyrészt így indexek 0-tól 4-ig futnak és a tömb közepén lévő 3x3x3-as kocka elemei kényelmesen – mátrixszerűen – indexelhetők 1-től 3-ig. Másrészt a tömb közepén lévő 3x3x3-as kocka minden elemére igaz, hogy egységesen van 26 db érvényesen indexelhető szomszédja. A 125 tömbelemből a széleken lévő 98 elem negatív számokkal feltölthető.
A szokásos i, j, k egységvektor rendszerben (koordináta-rendszerben) gondolkodva, i és j a képernyő síkját, k pedig a mélységet jelenti. A k-val 0-tól 4-ig „szeletelve” a tömböt, öt db négyzetet/mátrixot kapunk az alábbiak szerint. A színes tömbelemek negatív számokkal kerülnek feltöltésre, a kígyó útját határolják mindhárom irányból:
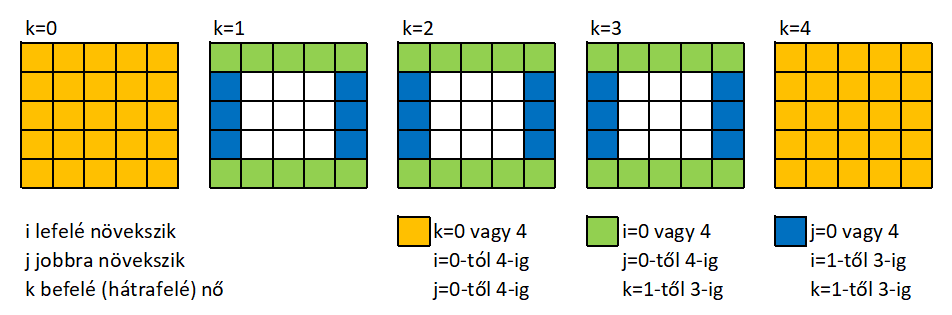
A belül lévő – fehér színű – 3x3x3-as kocka/tömb elemeit kezdőértékként célszerű 0-val feltölteni.
A szomszédos kockák kiválasztása során csak a középen lévő kocka 6 db lapszomszédját kell figyelembe venni. A középen lévő (a következő ábrán nem látszó) kocka három tengely szerinti 2-2-2 szomszédos kockája különböző színekkel jelölt.
Él- és csúcsszomszédság esetén nem tud tekeredni a kígyó. A forduláshoz/tekeredéshez legalább 3 – a kígyóban egymás utáni – kocka szükséges. Az aktuális kockának – pozíciójától függően – legfeljebb 6 lapszomszédja lehet. Ezt csökkenti, ha a kocka valamelyik csúcsban helyezkedik el, illetve menet közben is – ahogyan egyre hosszabb lesz a kígyó – folyamatosan csökken a még szabad elemek száma.
A megoldás során a belül lévő – fehér színű – 3x3x3-as kocka/tömb elemeit kell sorszámozni 1-től 27-ig, jelölve ezzel a kígyó útját. A kezdetben 0-val jelölt szabad elemek végül elfogynak.
Megállapodunk abban, hogy a kígyó az útját az (1, 1, 1) pozícióban kezdi és az 1 sorszámot kapja. Addig kell újabb szomszédos kockákat – egyesével haladva – kiválasztani módszeresen vagy véletlenszerűen próbálkozva, vagy akár visszalépéses algoritmussal is, amíg mind a 27 kiválasztásra kerül.
Megvalósítás
Létre kell hozni a háromdimenziós tömböt példányváltozóként:
int[][][] cube=new int[5][5][5];
A cubeInit() metódus kezdetben feltölti a tömb elemeit. A széleken lévő elemekbe különböző negatív értékek kerülnek, hogy jól megkülönböztethető legyen, melyik ciklus melyik pozíciókért felel. Másképpen is lehetne: például kezdetben minden elem -1, utána a belül lévők felülírhatók 0-val.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
private void cubeInit() { //k=0, k=4 for(int i=0; i<=4; i++) for(int j=0; j<=4; j++) { cube[0][i][j]=-1; cube[4][i][j]=-1; } //i=0, i=4 for(int j=0; j<=4; j++) for(int k=1; k<=3; k++) { cube[k][0][j]=-2; cube[k][4][j]=-2; } //j=0, j=4 for(int i=1; i<=3; i++) for(int k=1; k<=3; k++) { cube[k][i][0]=-3; cube[k][i][4]=-3; } //kocka belseje for(int k=1; k<=3; k++) for(int i=1; i<=3; i++) for(int j=1; j<=3; j++) cube[k][i][j]=0; cube[1][1][1]=1; } |
Hasznos a cubePlot() metódus, amellyel megjeleníthetők a konzolon a tömb elemei (állapota):
|
1 2 3 4 5 6 7 8 9 10 11 12 |
private void cubePlot(String message) { System.out.println(message); for(int i=0; i<=4; i++) { for(int j=0; j<=4; j++) { for(int k=0; k<=4; k++) System.out.print(String.format("%3d", cube[j][i][k])); if(j<4) System.out.print(" |"); } System.out.println(); } } |
A getNextNeighbour() függvény egydimenziós tömbként ( int[]) visszaadja a paramétereként átvett – x, y, z koordinátával jelölt – kocka egyik kiválasztott szomszédját, amely a kígyó útját jelöli. A kiválasztás történhet módszeresen vagy véletlenszerűen próbálkozva, vagy akár visszalépéses algoritmussal is. A metódus forráskódját most nem részletezem. A metódus felelős a kígyó helyes útvonaláért, azaz a kiválasztás során a kígyó nem rekedhet meg zsákutcában, másképpen nem haraphatja meg saját magát.
A vezérlést a run() metódus végzi el az alábbiak szerint:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
private void run() { cubeInit(); cubePlot("1. lépés:"); int count=1, i=1, j=1, k=1; while(count<27) { int[] rN=getNextNeighbour(i, j, k); i=rN[0]; j=rN[1]; k=rN[2]; count++; cube[i][j][k]=count; cubePlot(count+". lépés:"); } } |
Addig fut a ciklus, amíg a kígyó nem tölti ki a 3x3x3-as kockát (másképpen: amíg a kígyó nem éri el a maximális hosszúságot). A tömb állapotát kezdetben és lépésenként is kiíratja a vezérlő metódus a konzolra.
Konzolos eredmény
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
1. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 2. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 3. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 4. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 5. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 6. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 7. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 8. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 9. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 0 0 -3 | -3 9 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 10. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 0 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 11. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 12. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 13. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 14. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 15. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 16. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 17. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 17 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 18. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 0 -3 | -3 2 17 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 19. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 20. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 21. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 22. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 23. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 24. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 25. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 25 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 26. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 25 -3 | -3 8 11 26 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 27. lépés: -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -3 7 12 25 -3 | -3 8 11 26 -3 | -3 9 10 27 -3 | -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1 |
A konzolos eredmény előállításánál fontos volt, a tömb változásait tudjuk követni. Az összes negatív szám elhagyható lehet a kiírásból, ha meggyőződtünk az implementált algoritmus helyes működéséről. Átlátva a problémát, a megoldás könnyen elállítható egy grafikus és/vagy egy irányokat mutató jelölésrendszer szerint is, például:
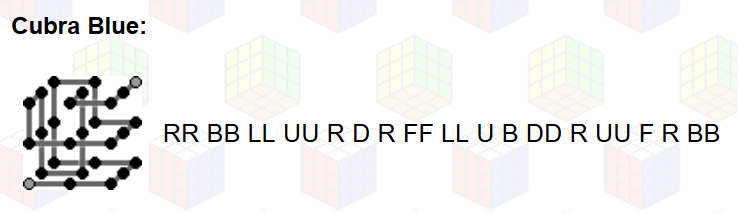
Hivatkozások
- Hogyan lehet megoldani az egyik kígyókockát? (képek+videó)
- A feladat általános megoldhatóságának izgalmas levezetése (gráfelmélet, Hamilton-kör):
Bent Hamilton Cycles in d-Dimensional Grid Graphs (2002),
Finding a Hamiltonian Path in a Cube with Specified Turns is Hard (2013) - Haskell nyelvű megoldás: Solving the Snake Cube Puzzle in Haskell
- Aki online vásárolna kígyókockát webáruházakból:
Fakopáncs, Amazon1, Amazon2, AliExpress - JavaScript kígyókocka
- Aki saját maga barkácsolna kígyókockát
- 4x4x3-as kígyókocka
- 4x4x4-es kígyókocka (anakonda)
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam tematikájához kötődik. Több alkalommal is tudunk ezzel a feladattal foglalkozni, attól függően, hogy a getNextNeighbour() függvény működését hogyan tervezzük és implementáljuk:
- A 13-16. óra: Tömbök témakör esetén a szomszédos kockák közül módszeresen – azonos sorrendben haladva a legfeljebb 6 lehetséges szomszéd közül – választjuk ki mindig az elsőt. Ekkor mindig ugyanazt az egyetlen helyes megoldást kapjuk meg.
- A 17-28. óra: Objektumorientált programozás témakör esetén atipikusan a kivételkezelést használhatjuk vezérlésre úgy, hogy a lehetséges szomszédos kockák közül mindig véletlenszerűen választunk. Ekkor a kígyó önmagába harapását úgy előzzük meg, hogy tömb túlindexelésekor keletkező kivételt benyeljük és újrakezdjük a feladatot mindaddig, amíg találunk egy olyan megoldást, aminek lépései közben nem keletkezik kivétel.
- Az orientáló modul 9-12. óra: Mesterséges intelligencia témakör esetén véletlenszerű kocka kiválasztási stratégiával rendelkező visszalépéses algoritmust specifikálhatunk és implementálhatunk. Ez lényegesen összetettebb feladat és mindig helyes megoldást ad több lehetséges megoldás közül.
Ez egy két részből álló blog bejegyzés 1. része. A blog bejegyzés 2. része itt található.
Rákattantunk a témára és barkácskodtunk a https://woodgears.ca/puzzles/snake_cube.html útmutatása szerint. Az ILIAS-os csoportba töltöttünk fel képeket. Elsőre nem lett olyan szép, de azután lefestettük. Hasznos volt, mert hosszú már a HO 🙂 és a fiúknak is az itthoni suli. Most már mind a hat nevesített példányt sikerült összeállítani és kirakni: https://www.jaapsch.net/puzzles/javascript/snakecubej.htm
OK Dániel, az ILIAS-os csoportban folytatjuk és meg is beszéljük a következő órán.
Láttam a képeket. Valahogy ide is lehet csatolni. Péter mutatta az órán, de nem írtam fel. Hihetetlenül alaposak és türelmesek voltatok. Náray Erika jutott eszembe, ő mondta egyszer: „karácsonykor minden gond nélkül lesütök két raklap mézeskalácsot, de ha kettőt fel kell díszíteni, akkor az ideg széthajít”. Lehet, hogy többet profitáltak belőle a fiúk, mint az utóbbi hetek online gimis technika óráiból.
Én a JS forráskódot böngésztem, de egyelőre elvesztem a matekban, ahogyan rajzol, de a blogban leírt algoritmust már értem.
Szuper Anikó! Örülök neki.
Kedvet kaptam:
– vettem egy 4*4*4-es anakondát. GoPro-val szétszedtem a biztonság kedvéért. Hasznos volt a videó, amikor elakadtam az összerakás közben. Kerestem és találtam hozzá megoldást, de nem teljesen ugyanolyan az én kockámban az útvonal, de nem jött rosszul: https://www.youtube.com/watch?v=L6A4xyyXezc
– írtam egy
getNextNeighbour()függvényt visszalépéses algoritmussal és 3*3*3 esetben jól működik. Szinte minden általános benne, de elakad, amikor megpróbáltam 4*4*4 méretben futtatni. Feltöltöttem ILIAS-ra, Sándor, megnéznéd a következő órára, mitől nem jó?Igen Dániel. Kíváncsi vagyok, meddig jutottál el ebben a nehéz feladatban. Ha van kedved, össze is foglalhatnád a csoportnak a gondolatmenetedet a következő órán.
F. Dániel: láttam az ILIAS-on a megoldásodat. Én is írtam egy visszalépéses megoldást, másféleképpen. Ha olyan pozícióból indul a kígyó, ahonnét nem kell az útvonalon háromnál többet visszalépni, akkor talál utat. Hosszabb visszalépésnél valami probléma van. Ilyen elakad a program. Megbeszéljük Discordon?
BPali: oké, szívesen, inkább személyesen, a következő pénteki óra előtt vagy után?
Örülök, hogy kooperáltok. Összefoglalnátok, hogy mire jutottatok? A kapcsolódó ILIAS fórumban vagy itt a blogon? Ha kell, Péter is tud segíteni a pénteki óra előtt/után.
Tudom, nem kígyókocka, de szívesen olvasnék a ti szemüvegetek keresztül a Rubik-kocka algoritmusairól. Például: CFOP kirakás. Péter: tervezitek, hogy programoztok ilyet és valamikor blogoltok róla?
Meglátjuk Nándor.
Egy Java EE alumni hallgatónk készített pet projektként korábban Rubik-kocka kirakó GUI-t Java 3D-ben, de csak visszalépéses algoritmust implementált. A csakot erősen idézőjelesen írtam, mert ez is kellően összetett volt, de nem külön nevesített, mint amire hivatkoztál. Addig is megpróbáljuk őt meghívni valamelyik következő rendezvényünkre: mutassa be ezt a projektjét.
Kristóf: én is próbálkoztam a visszalépéses algoritmussal. Rájöttem arra, hogy 1-2 visszalépés nem elég és elakad a megoldás. Hány visszalépéshez kellene adatokat tárolni, ami már elég lehet?
Endre: erre nincs általános képlet visszalépéses algoritmus esetén. Függ a feladattípus (kígyókocka) paramétereitől (méret: 3x3x3, 4x4x3, 4x4x4). A legrosszabb esetre is fel lehet/kell készülni. Ilyen például az:
Több olyan feladattípus is van (nem a kígyókocka), amelynél nem garantált, hogy a visszalépéses algoritmus terminál (eredményesen vagy sem, de befejeződik).
A 10 éves fiam megtervezte a Cubra Blue-féle kígyókockát labirintusként, 3D-ben. Ilyen lett:
Keresett hozzá egy fém golyót és megkérte az apját, hogy a golyóhoz méretezve nyomtassa ki neki a nemrég beszerzett 3D nyomtatón. Szóval rendesen inspirálódott a blogból.
Örülök Adrienn, hogy Máté ilyen lelkes volt és már itt tart. Ha lehet, akkor átlátszó filamentet használjatok hozzá.