A Pi-t (π) mindenki ismeri. Talán sokaknak kedvenc története is van a π-vel kapcsolatosan, amelyet iskolában vagy utazásai alatt szerzett. A π Euklidesz geometriájában a kör kerületének és átmérőjének arányát jelöli. A π irracionális szám, azaz végtelen, nem szakaszos tizedestört; másképpen számjegyei között nincs ismétlődés. A π értékével a hétköznapokban 3,14-dal szokás számolni, de a tudomány területén ennél sokkal pontosabb közelítést szokás alkalmazni. A π közelítése az informatikának köszönhetően akár több millió tizedesjegyig is lehetséges (például: S. Memphill: Pi to 1,000,000 places).
A nemzetközi Pi nap alkalmából (március 14) megvalósítottunk néhány – végtelen összeggel és szorzattal – π közelítésre való képletet, algoritmust Java nyelven.
1. Viète-féle sor
|
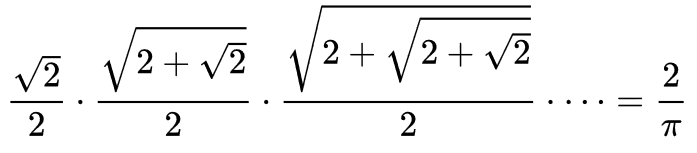
1 2 3 4 5 6 7 8 9 10 11 12 13 |
private static void megold1() { //Viète-féle sor double p=1, pi=1; for(int i=11; i>1; i--) { p=2; for(int j=1; j<i; j++) p=2+Math.sqrt(p); p=Math.sqrt(p); pi=pi*p/2; } pi*=Math.sqrt(2)/2; pi=2/pi; System.out.println(pi); } |
A módszer néhány eredménye: i=5 esetén 3.140331156954752 (2 tizedesjegyre pontos), i=10-nél 3.1415914215112 (5 tizedesjegyre pontos), i=11 esetén 3.1415923455701176 (6 tizedesjegyre pontos).
2. Leibniz-féle sor
|
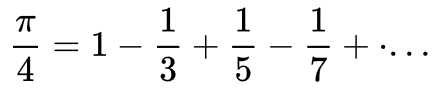
1 2 3 4 5 6 7 |
public static void megold2() { //Leibniz-féle sor double s=0; for(int i=0; i<=2500; i++) s+=Math.pow(-1, i)/(2*i+1); double pi=s*4; System.out.println(pi); } |
A módszer néhány eredménye: a 24. lépéstől stabil 1 tizedesjegyre, a 626. lépéstől stabil 2. tizedesjegyre, a 2453. lépéstől stabil 3 tizedesjegyre (hiszen alternál).
3. Wallis-formula
|
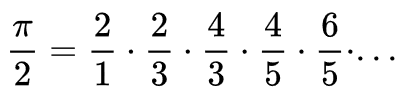
1 2 3 4 5 6 7 |
public static void megold3() { //Wallis-formula double p=1; for(int i=2; i<=17000; i+=2) p*=(1.0*i/(i-1)*(1.0*i/(i+1))); double pi=p*2; System.out.println(pi); } |
A módszer néhány eredménye: A 38. lépéstől 1, a 986. lépéstől 2, a 2650. lépéstől 3, a 16954. lépéstől már 4 tizedesjegyre pontos.
4. Csebisev-sor
|
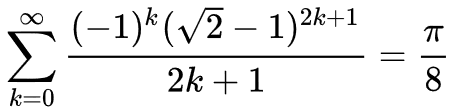
1 2 3 4 5 6 7 |
private static void megold8() { //Csebisev-sor, V1 double s=0; for(int k=0; k<=20; k++) s+=(Math.pow(-1, k)*Math.pow(Math.sqrt(2)-1, 2*k+1))/(2*k+1); double pi=s*8; System.out.println(pi); } |
A módszer k=10-re már 8 tizedesjegyig pontos.
A bejegyzéshez tartozó teljes forráskódot – további 8 közelítő módszer implementációjával együtt – ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 5-8. óra: Vezérlési szerkezetek alkalmához kötődik.
Az IThon.info is blogolt a Pi közelítésről:
https://ithon.info/blog/2019/03/18/programozono-pi-rekord/
Aki látta S. Rámánudzsan életéről szóló „Az ember, aki ismerte a végtelent” című 2015-ben megjelent amerikai-indiai-angol drámát, biztosan ismerős neki a Pi-t közelítő alábbi képlete:
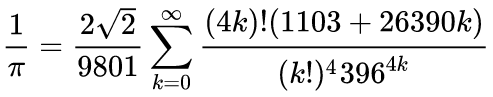
Ez a végtelen sor igen hatékonyan konvergál, már két tagra 17 pontos tizedesjegyet eredményez.
A film IMDb adatlapja: The Man Who Knew Infinity
Az megvan mindenkinek, hogy mivel a Pi végtelen hosszú, tartalmazza a világ összes TAJ számát, telefonszámát, bankszámlaszámát…?
És még az a mém, hogy a mérnököknek a Pi==3?
Igen, persze Roland. Ezek kihagyhatatlanok. 😉
Pi-versek is vannak, ez is külön műfaj:
Minden idők legjobb magyar nyelvű pi-verse
Köszönjük Angéla.