Címke: statisztika
11 blog bejegyzésnél szerepel:
 Doktoranduszok programoznak – újratöltve
Doktoranduszok programoznak – újratöltve
 Egy matematika érettségi feladat megoldása programozással 2021
Egy matematika érettségi feladat megoldása programozással 2021
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017
83 db hozzá kapcsolódó címke:
2017 (24), 2019 (24), 2020 (24), 2021 (24), 2023 (24), 2024 (8), adatbázis (25), algoritmus (31), animáció (17), ASCII (6), becslés (6), ciklusok (18), címkefelhő (2), csoportváltás (6), dátumkezelés (10), doktori képzés (4), élményalapú tanulás (21), elosztott alkalmazás (14), érettségi feladat (8), évforduló (24), fájlkezelés (29), fejtörő (11), fizika (7), funkcionális programozás (18), gamifikáció (33), Google Charts (5), grafika (26), grafikus felhasználói felület (40), hálózatkezelés (14), hatékonyság (28), hierarchikus lekérdezés (7), időzítő (4), Java forráskód (63), JDBC (12), JExcel API (4), JSON (4), kivételkezelés (13), kliensprogram (13), kockadobás (1), kódolás/dekódolás (6), kollekció (32), kombinatorika (7), közelítés (3), KSH (3), lambda kifejezés (13), lépésszám (9), logikai feladat (21), matematika érettségi feladat (8), matematika (30), mesterséges intelligencia (12), metódus (30), MVC (12), naptár (26), népesedési világnap (1), objektumorientált programozás (85), orientáló modul (39), öröklődés (16), péntek 13 (1), programozás (106), programozási tételek (28), projektmunka (5), rajzolás (15), rejtjelezés (3), rekurzió (9), Stream API (14), swing (26), szakmai modul (96), szimuláció (10), szófelhő (2), táblázat (11), tananyagfejlesztés (8), térinformatika (4), tervezés (41), tesztelés (21), titkosítás/visszafejtés (4), többféle megoldás összehasonlítása (37), tömb (17), toplista (5), továbbfejlesztés (23), továbbképzés (4), ünnepnap (13), worldometer (2), XML (8)









 Időnként készítünk oktatóprogramokat is tanfolyamainkon. Most az volt a cél, hogy kódolás/dekódolás szakterület egyik ismert betűkeveréses algoritmusának működését mutassa be lépésről-lépésre az oktatóprogram. A rácsrejtjelezést választottuk.
Időnként készítünk oktatóprogramokat is tanfolyamainkon. Most az volt a cél, hogy kódolás/dekódolás szakterület egyik ismert betűkeveréses algoritmusának működését mutassa be lépésről-lépésre az oktatóprogram. A rácsrejtjelezést választottuk.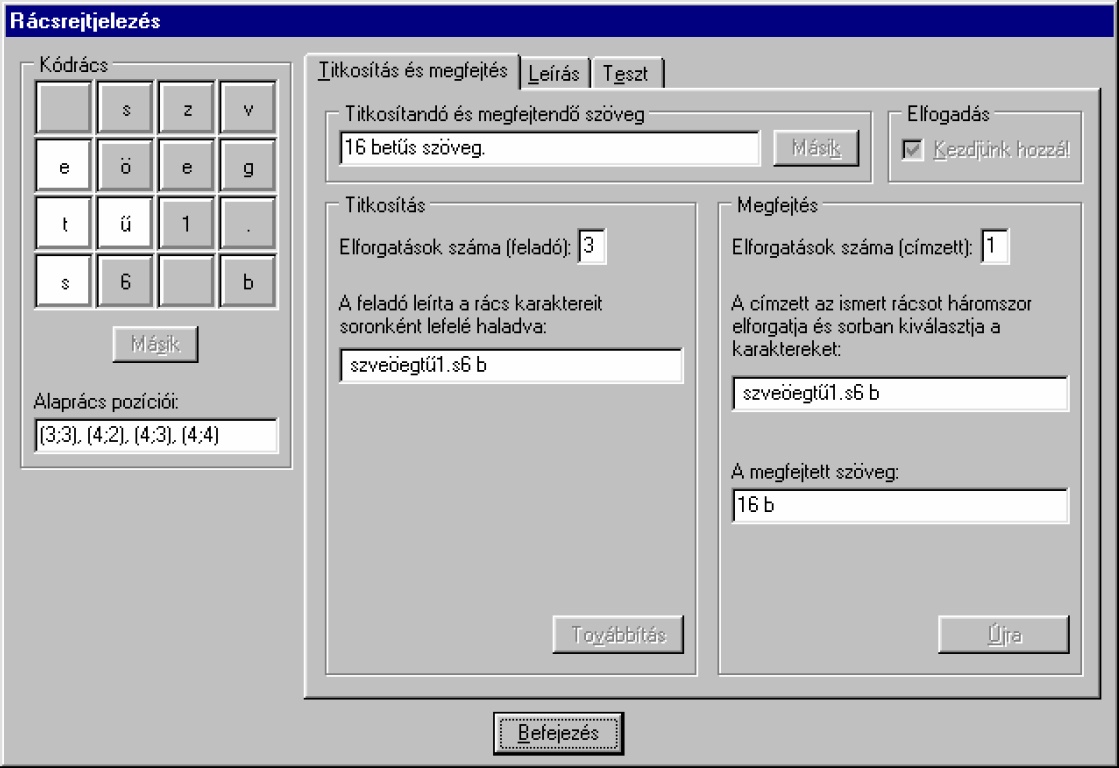
 Saját doktorandusz csoporttársaimmal én is többször beszélgettem már arról –
Saját doktorandusz csoporttársaimmal én is többször beszélgettem már arról – 
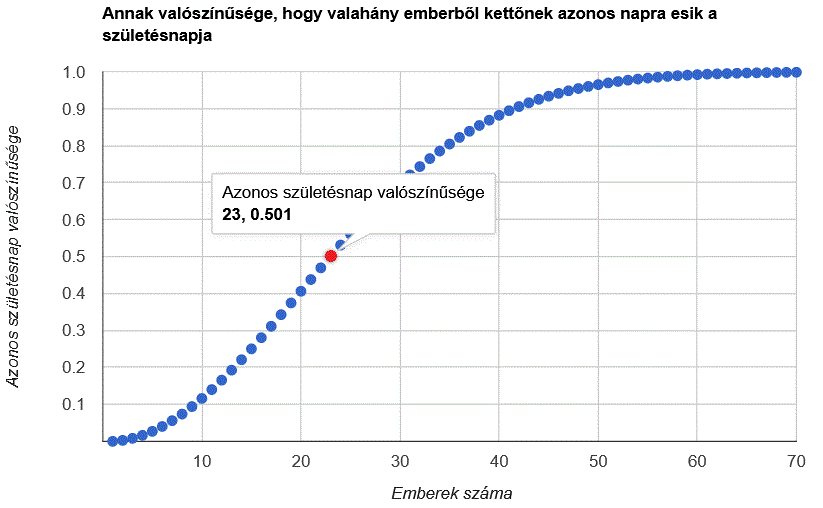
 A 2021-es középszintű matematika érettségi feladatsor 12. feladata inspirált arra, hogy a programozás eszköztárával oldjuk meg ezt a feladatot. Szükséges hozzá néhány programozási tétel: sorozatszámítás, eldöntés, megszámolás, kiválogatás. Többféle megoldás/megközelítés is előkerül. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az
A 2021-es középszintű matematika érettségi feladatsor 12. feladata inspirált arra, hogy a programozás eszköztárával oldjuk meg ezt a feladatot. Szükséges hozzá néhány programozási tétel: sorozatszámítás, eldöntés, megszámolás, kiválogatás. Többféle megoldás/megközelítés is előkerül. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az  Vajon hogyan kerül elő a Rómeó és Júlia az
Vajon hogyan kerül elő a Rómeó és Júlia az