A Fun Holidays – Fun, Wacky & Trivial Holidays weboldal sokféle különleges ünnepnapot listáz. Ezek leírása többnyire vicces, emlékezős, de néhány igazán érdekes, régi-régi hagyományt elevenít fel.
Ma van (november 23.) a Fibonacci nap. Fibonacci középkori matematikus volt, ő tette közismertté a Fibonacci-sorozat-ot. A (0), 1, 1, 2, 3, 5, 8, 13, 21, 34, … sorozat igen népszerű azok közében is, akik programozást tanulnak. A sorozat első két eleme 1 és 1 (ha szükséges, akkor nulladik elemmel is dolgozhatunk), és minden további elem az előző két elem összege. Többféle történet is fűződik ehhez, talán az egyik legismertebb a nyúlpárok szaporodásához kötődik.
Honnan származik a Fibonacci nap? A mai nap hh.nn. formátumban 11.23. , és a számjegyek részei a Fibonacci-sorozatnak. Mindössze ennyi, ilyen egyszerű. 😉
A sorozat elemei könnyen előállíthatók néhány változó használatával. Ha a kezdő programozó már ismeri a ciklust – algoritmikus építőelemként –, akkor ez az iteratív megoldás. A rekurzív megoldás tipikus rossz megoldásként ismert. Lássuk az utóbbi Java megvalósítását:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public class FibTeszt { final static int N=5; static int fib(int n) { for(int i=1; i<=N-n; i++) System.out.print("-"); System.out.println("fib("+n+")"); if(n<2) return n; return fib(n-1)+fib(n-2); } public static void main(String[] args) { System.out.println(fib(N)); } } |
Ha kiadnám a fenti Java forráskódot papíron ezt egy dolgozatban, zárthelyin, állásinterjú szakmai részén azzal a kérdéssel, hogy mit ír ki a program a képernyőre, akkor bizony sokan bajban lennének. Meg is történt ez már sokszor, tapasztalatból írom. A rekurzió első leszálló ágáig szinte mindenki eljut, de az ott induló első felszálló ágat követően sokan belezavarodnak a részlépések egymásutániságába. A végeredményt szinte mindenki tudja, de itt most arra helyezzük a hangsúlyt, hogy hogyan jutunk el odáig. Persze n=5-re fib(5)=5. Alig fordult még elő, hogy valaki hibátlanul leírta volna az alábbi eredményt:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
fib(5) -fib(4) --fib(3) ---fib(2) ----fib(1) -----fib(0) ----fib(1) ---fib(2) ----fib(1) -----fib(0) --fib(3) ---fib(2) ----fib(1) -----fib(0) ----fib(1) 5 |
A megoldás során – emlékeztetek arra, hogy ez atipikus megközelítés – sok-sok redundáns lépés történik. Hiszen például a fib(3)-at tudni kell a fib(4)-hez és a fib(5)-höz is, hiszen fib(4)=fib(2)+fib(3) és fib(5)=fib(3)+fib(4), valamint ebben az implementációban nincs semmilyen emlékezet (puffer, adatszerkezet), amivel a sok feleslegesnek vélhető számítást elkerülhetnénk.
Nyert ügye lehet annak, aki „fejben összerakja” az alábbi fát – akár dinamikusan, menet közben hozzáadva és törölve elemeket – és ebben navigálva (ezt bejárva) válaszolja meg a kérdést:
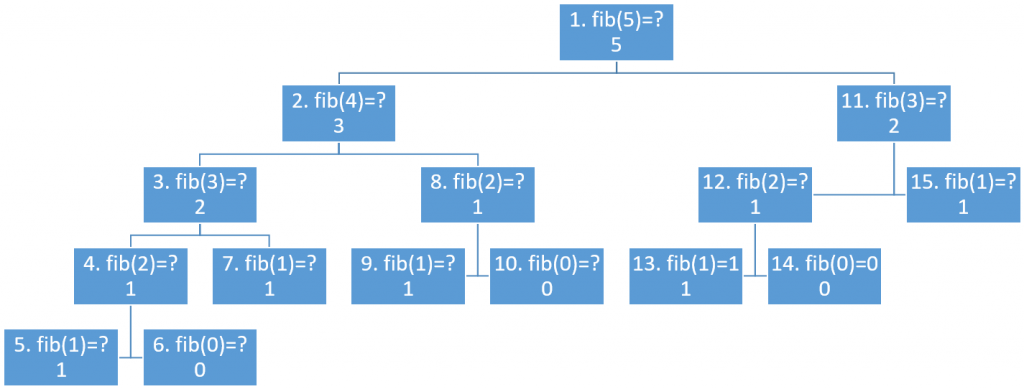
Az alábbi animáció segíthet a megértésben. 45 lépésben mutatja be az aktuális részlépést/részfeladatot (leszálló ág) és/vagy az aktuális részeredményt (felszálló ág):
A Fibonacci-sorozat többféleképpen kapcsolódik a természethez, természeti jelenséghez, növényekhez, állatokhoz. Például: virágszirmok száma, levelek elfordulása, napraforgók magjai, fenyőtoboz pikkelyei, nautilus háza, aranymetszés, zenei hangolás, zeneművek tagolása). A Fibonacci-sorozat felhasználható algoritmusok futási idejének becsléséhez, fa adatszerkezetek építéséhez is. Az aranymetszésről megoszlanak a vélemények. Vannak akik szinte mindenben ezt látják (művészet: festészet, szobrászat), mások módszeresen cáfolják ezt. Utóbbira példa Falus Róbert: Az aranymetszés legendája, Magyar Könyvklub, 2001, második, javított kiadás, ISBN 963-547-332-X.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió alkalmához kötődik.
Nekem tetszettek és megosztom:
Fibonacci Sequence (a sorozat és az aranymetszés kapcsolata):
https://www.mathsisfun.com/numbers/fibonacci-sequence.html
The AMAZING Fibonacci Spiral/Sequence – Extended Version! (látványos videó):
https://www.youtube.com/watch?v=Y1VL1g2Gg6o
Fibonacci Sequence—A Handy Mathematical Approach For Looking At Evolution! (innovatív foglalkozásokhoz ötletek):
https://www.sciencefriday.com/educational-resources/fibonacci-sequence-handy-mathematical-approach-looking-evolution/
Identities involving Fibonacci Series (sok-sok gondolkodtató feladattal):
https://brilliant.org/wiki/fibonacci-series/
Köszönöm Péter. Hasznos ötleteket adtál egy következő Fibonacci naphoz. 😉
Péter: készíthetnénk egy GUI-s animációs programot a 2020-as Fibonacci naphoz kötődően. Például a Fibonacci-spirál lépésenként/fázisonként GUI-n megvalósítva. Van kedved?
Sanyi: OK. Találjuk ki, hogy asztali swing legyen, vagy böngészőben fusson. Beleépíthetnénk valamilyen távirányítóhoz hasonló vezérlést a fázisok közötti váltáshoz: Első, Előző, Következő, Utolsó. Augusztus első szombatján ráérek.
Péter: rendben.
Nagy küzdelem ez a rekurzió. Hogy lehet ezt könnyen megérteni?
Endre: ezt nem tudom megválaszolni egy hozzászólásban. Ez egy összetett kérdés/probléma. A programozás tanításának egy nagy kihívása. Kapcsolódik a matematikában a teljes indukcióhoz. A kontakt óráinkon mutatunk sok-sok mintapéldát, összehasonlítjuk néhány alapfeladat, programozási tétel ciklussal való megoldását (iteratív) a ciklus nélküli megoldással (rekurzív). Megnézünk néhány tipikus és atipikus rekurzív megoldást. Lépésenként futtatunk forráskódot és közben figyeljük: melyik változóval mi történik, hol jár a végrehajtás. A rekurzió – mint elv, algoritmus, gondolatmenet – nem csupán az utasítás végrehajtás kódolása során van a fejlesztők fejében, hanem adatszerkezetek felépítésénél, feldolgozásánál (például: fa és bejárása) is.
Hasznos volt, hogy átbeszéltük szombaton. El is készültem vele. Időzítettem a blog bejegyzést az idei Fibonacci napra, azaz 2020.11.23-ra.
Ma megjelent Péter blog bejegyzése: Fibonacci-spirál
Ma Balázs is blogolt a Fibonacci-sorozatról, hiszen ma újra Fibonacci nap van. Az atipikus rekurzív megközelítés szép alternatíváját adja a Binet-formula, amihez nem kell sorozat (és hozzá adatszerkezet/tárhely) és nem kell ismerni az n-edik elem kiszámításához az előző két elemet sem. Íme: https://it-tanfolyam.hu/fibonacci-sorozat/