 A Fun Holidays – Fun, Wacky & Trivial Holidays weboldal sokféle különleges ünnepnapot listáz. Ezek leírása többnyire vicces, emlékezős, de néhány igazán érdekes, régi-régi hagyományt elevenít fel.
A Fun Holidays – Fun, Wacky & Trivial Holidays weboldal sokféle különleges ünnepnapot listáz. Ezek leírása többnyire vicces, emlékezős, de néhány igazán érdekes, régi-régi hagyományt elevenít fel.
Ma van (november 23.) a Fibonacci nap. Fibonacci középkori matematikus volt, ő tette közismertté a Fibonacci-sorozat-ot. A
(0), 1, 1, 2, 3, 5, 8, 13, 21, 34, … sorozat igen népszerű azok közében is, akik programozást tanulnak. A sorozat első két eleme
1 és
1 (ha szükséges, akkor nulladik elemmel is dolgozhatunk), és minden további elem az előző két elem összege. Többféle történet is fűződik ehhez, talán az egyik legismertebb a nyúlpárok szaporodásához kötődik.
Honnan származik a Fibonacci nap? A mai nap
hh.nn. formátumban
11.23. , és a számjegyek részei a Fibonacci-sorozatnak. Mindössze ennyi, ilyen egyszerű. 😉
A sorozat elemei könnyen előállíthatók néhány változó használatával, ha a kezdő programozó már ismeri a ciklust, mint algoritmikus építőelem – ez az iteratív megoldás. A rekurzív megoldás tipikus rossz megoldásként ismert, lássuk ennek Java megvalósítását:
|
|
public class FibTeszt { final static int N=5; static int fib(int n) { for(int i=1; i<=N-n; i++) System.out.print("-"); System.out.println("fib("+n+")"); if(n<2) return n; return fib(n-1)+fib(n-2); } public static void main(String[] args) { System.out.println(fib(N)); } } |
Ha kiadnám a fenti Java forráskódot papíron ezt egy dolgozatban, zárthelyin, állásinterjú szakmai részén azzal a kérdéssel, hogy mit ír ki a program a képernyőre, akkor bizony sokan bajban lennének. Meg is történt ez már sokszor, tapasztalatból írom. A rekurzió első leszálló ágáig szinte mindenki eljut, de az ott induló első felszálló ágat követően sokan belezavarodnak a részlépések egymásutániságába. A végeredményt szinte mindenki tudja, de itt most arra helyezzük a hangsúlyt, hogy hogyan jutunk el odáig. Persze
n=5-re
fib(5)=5. Alig fordult még elő, hogy valaki hibátlanul leírta volna az alábbi eredményt:
|
|
fib(5) -fib(4) --fib(3) ---fib(2) ----fib(1) -----fib(0) ----fib(1) ---fib(2) ----fib(1) -----fib(0) --fib(3) ---fib(2) ----fib(1) -----fib(0) ----fib(1) 5 |
A megoldás során – emlékeztetek arra, hogy ez atipikus megközelítés – sok-sok redundáns lépés történik. Hiszen például a
fib(3)-at tudni kell a
fib(4)-hez és a
fib(5)-höz is, hiszen
fib(4)=fib(2)+fib(3) és
fib(5)=fib(3)+fib(4), valamint ebben az implementációban nincs semmilyen emlékezet (puffer, adatszerkezet), amivel a sok feleslegesnek vélhető számítást elkerülhetnénk.
Nyert ügye lehet annak, aki „fejben összerakja” az alábbi fát – akár dinamikusan, menet közben hozzáadva és törölve elemeket – és ebben navigálva (ezt bejárva) válaszolja meg a kérdést:
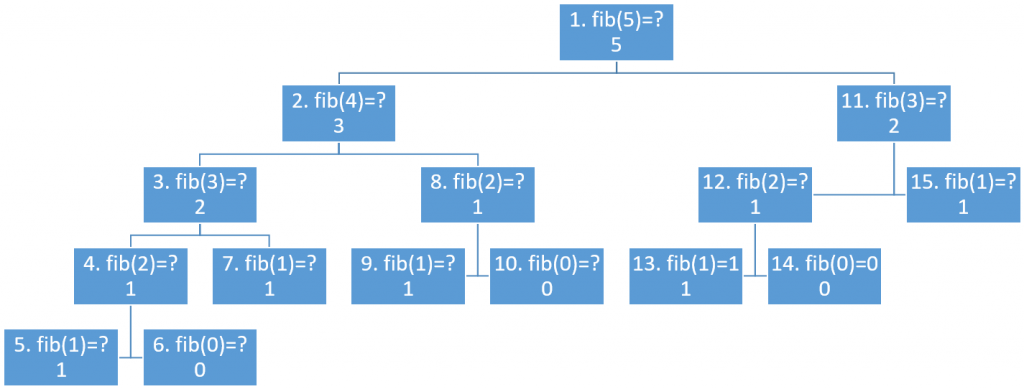
Az alábbi animáció segíthet a megértésben: 45 lépésben mutatja be az aktuális részlépést/részfeladatot (leszálló ág) és/vagy az aktuális részeredményt (felszálló ág):

A Fibonacci-sorozat többféleképpen kapcsolódik a természethez, természeti jelenséghez, növényekhez, állatokhoz (virágszirmok száma, levelek elfordulása, napraforgók magjai, fenyőtoboz pikkelyei, nautilus háza, aranymetszés, zenei hangolás, zeneművek tagolása), felhasználható algoritmusok futási idejének becsléséhez, fa adatszerkezetek építéséhez is. Az aranymetszésről megoszlanak a vélemények: vannak akik szinte mindenben ezt látják (művészet: festészet, szobrászat), mások módszeresen cáfolják ezt (például Falus Róbert: Az aranymetszés legendája, Magyar Könyvklub, 2001, második, javított kiadás, ISBN 963-547-332-X).
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió alkalmához kötődik.




 Az elmúlt 20 évben rengeteg logikai feladatokból álló tesztet állítottam össze. Kezdetben iskolai szakkörökhöz, versenyekre való felkészítéshez, tehetséggondozáshoz használtam ezeket. Ezután következett a Logikus gondolkodásra nevelő Diákműhely, amelyben ez már professzionális lett. Végül több cég/vállalkozás számára állítottam össze többféle programozói, szoftverfejlesztői tanfolyam tematikájához illeszkedően toborzáshoz, felvételihez, jelentkeztetéshez, kiválogatáshoz, szakmai interjúk során használható tesztet/feladatsort. Ezek eltérő igények szerint mérik/skálázzák a logikus gondolkodást, a problémamegoldást, az algoritmikus készségek meglétét, az összefüggések/szabályok felismerésének és alkalmazásának szintjét, a szakmai felkészültséget.
Az elmúlt 20 évben rengeteg logikai feladatokból álló tesztet állítottam össze. Kezdetben iskolai szakkörökhöz, versenyekre való felkészítéshez, tehetséggondozáshoz használtam ezeket. Ezután következett a Logikus gondolkodásra nevelő Diákműhely, amelyben ez már professzionális lett. Végül több cég/vállalkozás számára állítottam össze többféle programozói, szoftverfejlesztői tanfolyam tematikájához illeszkedően toborzáshoz, felvételihez, jelentkeztetéshez, kiválogatáshoz, szakmai interjúk során használható tesztet/feladatsort. Ezek eltérő igények szerint mérik/skálázzák a logikus gondolkodást, a problémamegoldást, az algoritmikus készségek meglétét, az összefüggések/szabályok felismerésének és alkalmazásának szintjét, a szakmai felkészültséget.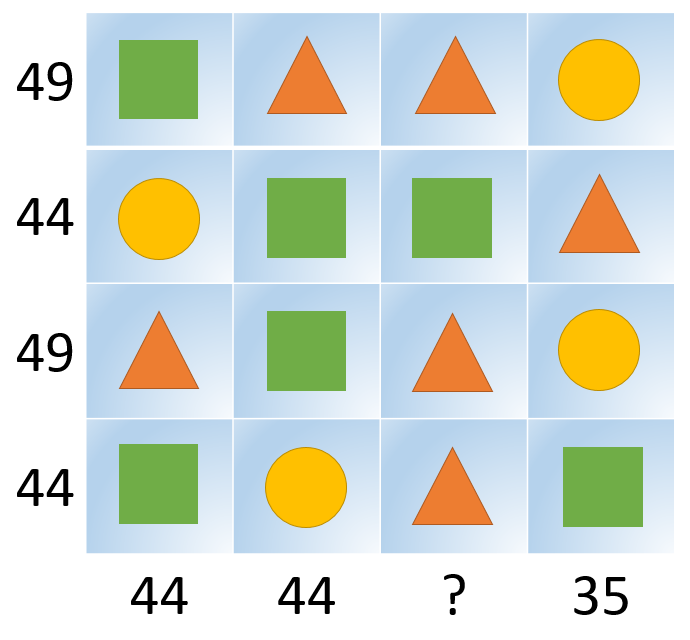
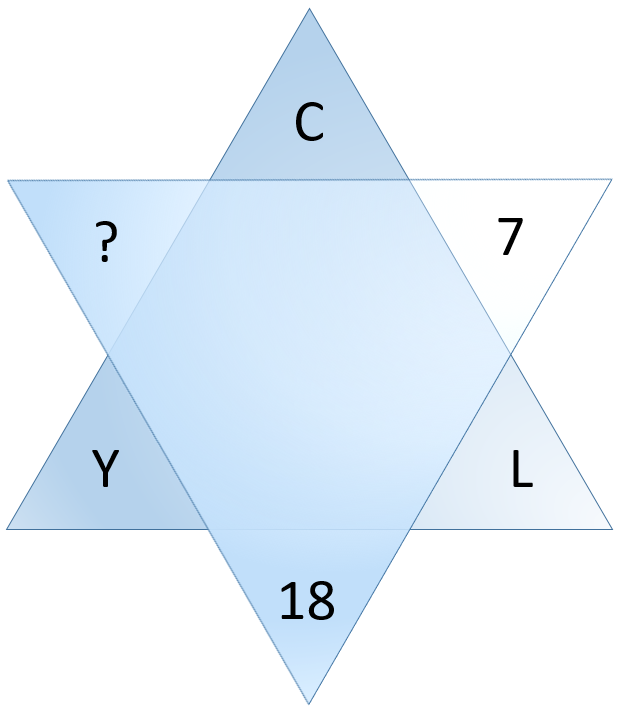
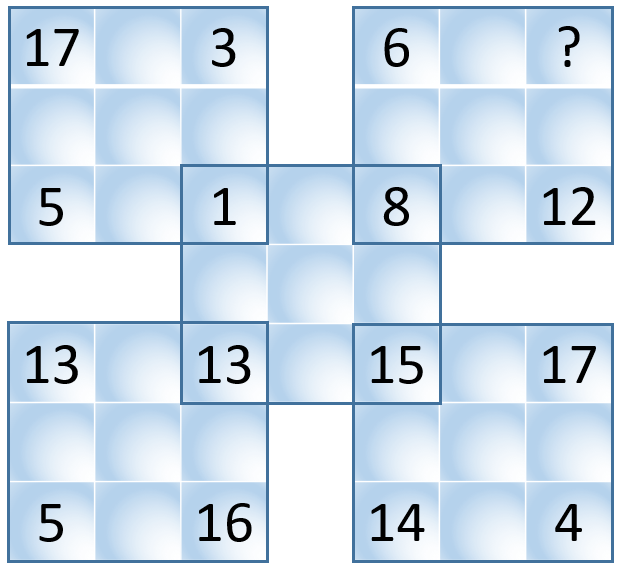


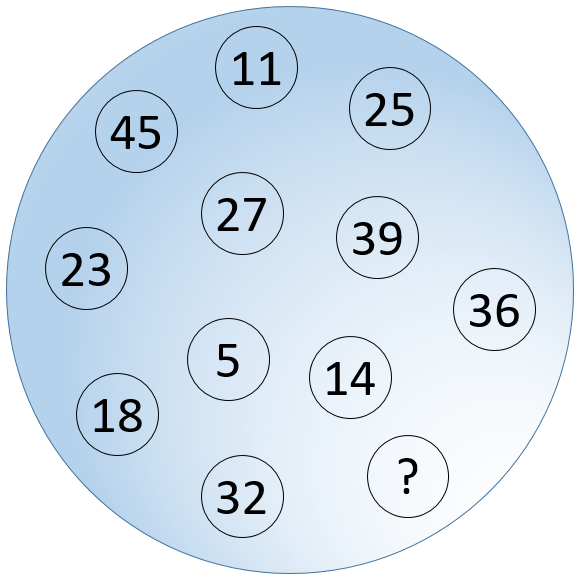
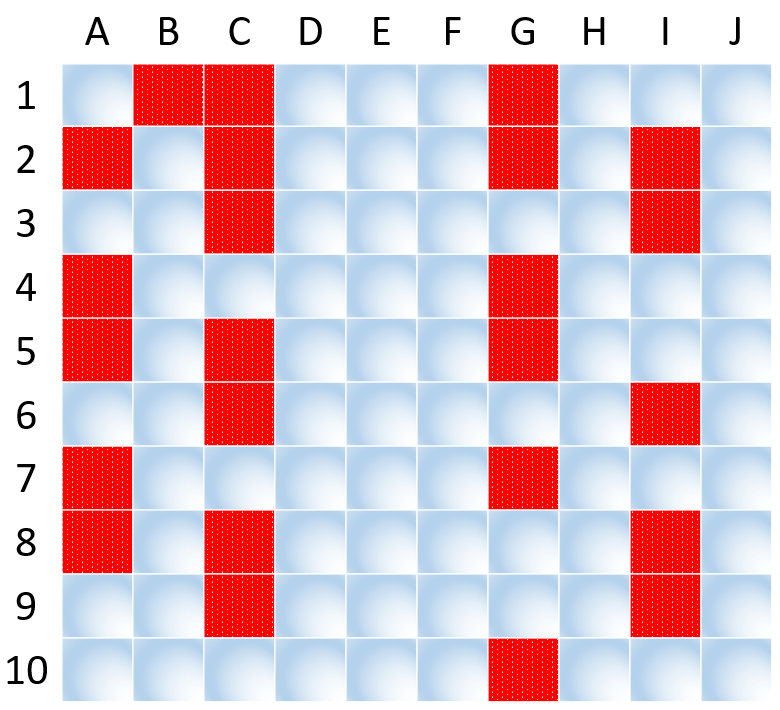



 A
A 

 Most nem a híres kisvonatról van szó, hanem egy ismert kriptoaritmetikai feladványról. Ebben a feladattípusban egyszerű matematikai műveletek szerepelnek és a különböző betűk különböző számjegyeket jelölnek. Általában többféleképpen megoldhatók: intuíció, ötlet, módszeres próbálkozás, következtetés, kizárás vagy klasszikus behelyettesítés. Ha van megoldás és meg is találunk egyet, akkor a következő kérdés az, hogy van-e még, illetve összesen hány megoldás van?
Most nem a híres kisvonatról van szó, hanem egy ismert kriptoaritmetikai feladványról. Ebben a feladattípusban egyszerű matematikai műveletek szerepelnek és a különböző betűk különböző számjegyeket jelölnek. Általában többféleképpen megoldhatók: intuíció, ötlet, módszeres próbálkozás, következtetés, kizárás vagy klasszikus behelyettesítés. Ha van megoldás és meg is találunk egyet, akkor a következő kérdés az, hogy van-e még, illetve összesen hány megoldás van?