Címke: ünnepnap
13 blog bejegyzésnél szerepel:
76 db hozzá kapcsolódó címke:
2017 (24), 2018 (24), 2020 (24), 2021 (24), 2022 (24), 2023 (24), 2024 (8), algoritmus (31), animáció (17), atipikus megoldás (5), becslés (6), ciklusok (18), címkefelhő (2), dátumkezelés (10), életrajz (4), évforduló (24), fájlkezelés (29), fejtörő (11), felvételi feladat (4), Fibonacci (3), funkcionális programozás (18), gamifikáció (33), Google Charts (5), grafika (26), grafikus felhasználói felület (40), hálózatkezelés (14), hatékonyság (28), húsvétvasárnap (1), IT történet (20), Java forráskód (63), JSON (4), kliens-szerver (7), kliensprogram (13), kollekció (32), kombinatorika (7), közelítés (3), KSH (3), lambda kifejezés (13), lépésszám (9), logikai feladat (21), matematika (30), megemlékezés (2), metódus (30), MVC (12), naptár (26), népesedési világnap (1), nőnap (1), objektumorientált programozás (85), operációs rendszerek (2), öröklődés (16), péntek 13 (1), Pi nap (2), Pi (2), programozás (106), programozási tételek (28), projektmunka (5), rajzolás (15), rekurzió (9), statisztika (11), Stream API (14), swing (26), szakmai modul (96), szálkezelés (4), szófelhő (2), télapó probléma (1), térinformatika (4), tervezés (41), tesztelés (21), többféle megoldás összehasonlítása (37), tömb (17), toplista (5), továbbfejlesztés (23), transzformáció (8), videó (5), worldometer (2), XML (8)









 A
A 
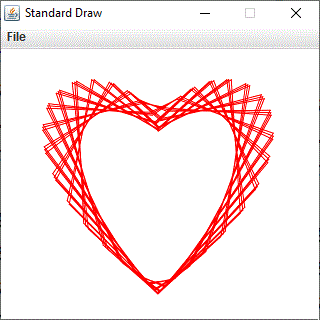
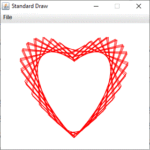 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.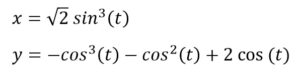


 Ma van (november 23.) a Fibonacci nap (újra).
Ma van (november 23.) a Fibonacci nap (újra). 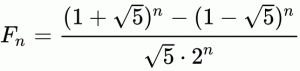
 Vajon hogyan kerül elő a Rómeó és Júlia az
Vajon hogyan kerül elő a Rómeó és Júlia az