Címke: 2017
24 blog bejegyzésnél szerepel:
 Programozási Hét 2017 – CodeWeek.eu
Programozási Hét 2017 – CodeWeek.eu
 HWSW – Merre tart a Java? Nyár végi Java fejlesztői meetup
HWSW – Merre tart a Java? Nyár végi Java fejlesztői meetup
 Ismerkedjünk lambda kifejezésekkel!
Ismerkedjünk lambda kifejezésekkel!
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017
 Hogyan értékeljük az online vizsgafeladatot?
Hogyan értékeljük az online vizsgafeladatot?
110 db hozzá kapcsolódó címke:
adatbázis (25), algoritmus (31), alkalmazottak életpálya modellje (3), alkalmazottak fizetése (4), alkalmazottak munkaköre (6), álláskeresés (17), animáció (17), Applet (1), atipikus megoldás (5), becslés (6), brute force (7), ciklusok (18), CodeWeek.eu (7), csoportváltás (6), dátumkezelés (10), Digitális Témahét (8), életpálya modell (3), életrajz (4), előadás műhely-napon (24), eredménytábla (10), érettségi feladat (8), értékelési szempont (6), Euler (3), évforduló (24), fájlkezelés (29), fejtörő (11), felvételi feladat (4), Fibonacci (3), funkcionális programozás (18), gamifikáció (33), grafika (26), grafikus felhasználói felület (40), hatékonyság (28), hexadecimális (2), hierarchikus lekérdezés (7), húsvétvasárnap (1), HWSW (4), idézet (10), ingyenes esemény (34), IT történet (20), játék (9), Java forráskód (63), JavaFX (3), JDBC (12), JFreeChart (7), JSP (3), karrier (17), karrierváltás (14), kígyókocka (2), kivételkezelés (13), kliens-szerver (7), kliensprogram (13), kockadobás (1), kollekció (32), kombinatorika (7), könyvajánló (4), közelítés (3), kriptoaritmetika (2), Kutatók éjszakája (8), lambda kifejezés (13), lekérdezés (18), lépésszám (9), logikai feladat (21), matematika érettségi feladat (8), matematika (30), megemlékezés (2), metódus (30), munkaerőpiac (14), MVC (12), naptár (26), nőnap (1), online vizsgafeladat (2), objektumorientált programozás (85), operációs rendszerek (2), Oracle HR séma (12), organogram (2), orientáló modul (39), öröklődés (16), összefoglalás (2), pályaorientáció (28), péntek 13 (1), programozás (106), Programozási Hét (7), programozási tételek (28), rajzolás (15), rekurzió (9), rendezvény 2017 (5), Servlet (1), soft skill (10), SQL forráskód (12), statisztika (11), Stream API (14), swing (26), szakmai előadás (31), szakmai modul (96), szálkezelés (4), szimuláció (10), táblázat (11), télapó probléma (1), tervezés (41), tesztelés (21), többféle megoldás összehasonlítása (37), tömb (17), továbbfejlesztés (23), transzformáció (8), ünnepnap (13), vélemény (4), videó (5), visszajelzés (5), XML (8)















 Az operációs rendszerek tervezésének fontos része az ütemezési, erőforrás- és szálkezelési feladatok problémamentes, holtpontmentes megoldása, szinkronizálása, amiről sok ismert szerző publikált már, néhányan közülük angol nyelven:
Az operációs rendszerek tervezésének fontos része az ütemezési, erőforrás- és szálkezelési feladatok problémamentes, holtpontmentes megoldása, szinkronizálása, amiről sok ismert szerző publikált már, néhányan közülük angol nyelven:  A
A 

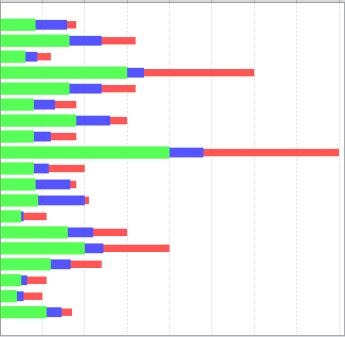
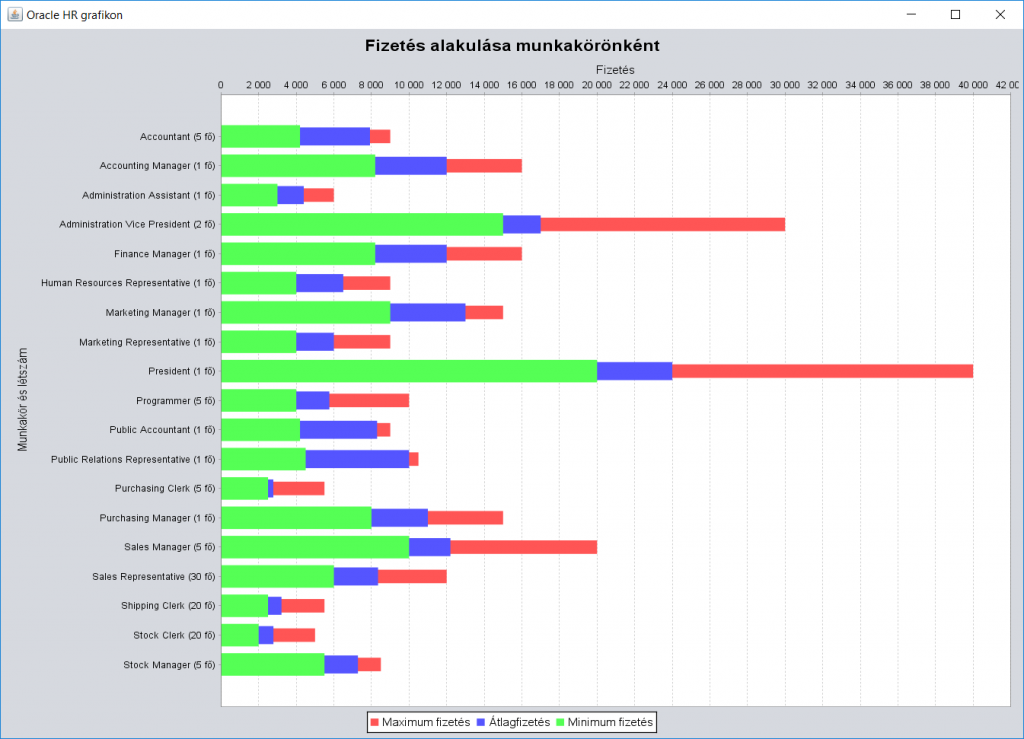
 XML formátumban megkapott adatokat grafikonon jelenítünk meg. 5 összetartozó adat/tulajdonság sorozatát dolgozzuk fel:
XML formátumban megkapott adatokat grafikonon jelenítünk meg. 5 összetartozó adat/tulajdonság sorozatát dolgozzuk fel:
 Sokan szerencsés vagy balszerencsés napnak tartják a péntek tizenharmadikát. Évente 1-2-3 alkalommal megtörténik, hogy a hónap 13. napja péntekre esik (minden vasárnap kezdődő hónapban). A hónap 13. napja valamivel valószínűbben péntekre esik, mint a hét bármely más napja. Átlagosan 212,35 naponként fordul elő péntek 13. Előfordulhat két egymást követő hónapban is, de akár 14 hónap is eltelhet két péntek 13 között.
Sokan szerencsés vagy balszerencsés napnak tartják a péntek tizenharmadikát. Évente 1-2-3 alkalommal megtörténik, hogy a hónap 13. napja péntekre esik (minden vasárnap kezdődő hónapban). A hónap 13. napja valamivel valószínűbben péntekre esik, mint a hét bármely más napja. Átlagosan 212,35 naponként fordul elő péntek 13. Előfordulhat két egymást követő hónapban is, de akár 14 hónap is eltelhet két péntek 13 között.