Ma van (november 23.) a Fibonacci nap (újra). Fibonacci középkori matematikus volt, ő tette közismertté a Fibonacci-sorozat-ot. A
(0), 1, 1, 2, 3, 5, 8, 13, 21, 34, … sorozat igen népszerű azok közében is, akik programozást tanulnak. A sorozat első két eleme
1 és
1 (ha szükséges, akkor nulladik elemmel is dolgozhatunk), és minden további elem az előző két elem összege.
Korábban is blogoltak a kollégáim a témában:
- Kaczur Sándor: Fibonacci nap,
- Balogh Péter: Fibonacci-spirál.
Következzen most az én öt különböző megoldásom Java forráskódja, rövid magyarázattal. Mindegyik a Fibonacci-sorozat első tíz elemét állítja elő.
1. megoldás
|
1 2 3 4 5 6 7 8 9 |
private void solution1(int n) { System.out.println("Az első "+n+" Fibonacci szám:"); List<Integer> list=new ArrayList<>(); list.add(1); list.add(1); for(int i=2; i<n; i++) list.add(list.get(i-1)+list.get(i-2)); System.out.println(list); } |
Az első megoldás generikus listát épít. Az első két elemet elhelyezi a lista elején ( list.add(1)). Ezek a lista nulladik és első elemei lesznek. Ezután a metódus a maradék 8 elemmel 2-től n-1-ig fiktív indexként hivatkozva az előző két elem összegeként ( list.get(i-1)+list.get(i-2)) index nélkül bővíti a listát.
2. megoldás
|
1 2 3 4 5 6 7 8 9 10 11 |
private static int fib(int n) { if(n<=1) return n; return fib(n-1)+fib(n-2); } private void solution2(int n) { System.out.println("Az első "+n+" Fibonacci szám:"); for(int i=1; i<=n; i++) System.out.println(fib(i)); } |
A második megoldás a tipikusan nem hatékony rekurzív módszert implementálja. A rekurzív fib() függvény a sorozat egyetlen elemét adja vissza, amit (a függvényt) a ciklus sokszor meghív ahelyett, hogy a ciklus vagy a rekurzió „emlékezne” az előző elemekre.
3. megoldás
|
1 2 3 4 5 6 7 8 |
private void solution3(int n) { System.out.println("Az első "+n+" Fibonacci szám:"); Stream.iterate( new int[] {0, 1}, f->new int[] {f[1], f[0]+f[1]}). limit(n). map(f->f[1]). forEach(System.out::println); } |
A harmadik megoldás funkcionális nyelvi elemeket (Stream API) használ. A folyamba kétdimenziós tömbre történő hivatkozással ( …f-> new int[]… ), közvetlen hozzárendeléssel/leképezéssel ( map()), kerülnek be a sorozat elemei.
4. megoldás
|
1 2 3 4 5 6 7 8 9 |
private void solution4(int n) { System.out.println("Az első "+n+" Fibonacci szám:"); final double SQRT5=Math.sqrt(5); for(int i=1; i<=n; i++) { int f=(int)((Math.pow(1+SQRT5, i)-Math.pow(1-SQRT5, i))/ (SQRT5*Math.pow(2, i))); System.out.println(f); } } |
A negyedik megoldás a Fibonacci-számok zárt alakját használja. Másképpen ez a Binet-formula:
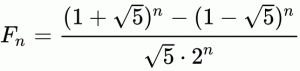
Ezzel a képlettel a sorozat elemei közvetlenül megadhatók, azaz nem szükséges más elemekre való hivatkozás. A ciklus adja meg, hogy a sorozat 1-10-ig indexelt elemei szükségesek.
5. megoldás
|
1 2 3 4 5 6 7 8 9 |
private void solution5(int n) { System.out.println("5 Az első "+n+" Fibonacci szám:"); final double SQRT5=Math.sqrt(5); IntStream.iterate(1, i->i+1). limit(n). map(i->(int)((Math.pow(1+SQRT5, i)-Math.pow(1-SQRT5, i))/ (SQRT5*Math.pow(2, i)))). forEach(System.out::println); } |
Az ötödik megoldás szintén Stream API-t használ. Először előállít egy sorozatot 1-10-ig, amiket a leképezésnél ( map()) inputként használ és alkalmazza rájuk a Binet-formulát. Hagyományos ciklus utasítás nem szükséges.
Eredmény
Mindegyik megoldás a konzolra írja szövegesen az eredményt, azaz a Fibonacci-sorozat első tíz elemét: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Érdemes elemezni a hatékonyság klasszikus három szempontja (időigény/lépésszám, tárigény, bonyolultság) alapján a különböző megoldásokat. Ezek mérésével könnyen kiegészíthetők a fenti metódusok, vagy az azokat meghívó osztályban a vezérlés.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió és 17-28. óra Objektumorientált programozás alkalmaihoz kötődik.
Erős ütőkártya ez a matek. Főleg a 4. megoldásnál használt Binet-formula. Eredeti alakja ebben a bizonyításban szerepel: https://www.milefoot.com/math/discrete/sequences/binetformula.htm
Így van Attila. Én már a formula kissé átrendezett, optimalizált változatát használtam. Ezt „kényelmesebb” kiszámolni.