A 2017-es középszintű matematika érettségi feladatsor 12. feladata inspirált egy Java program megírására. Szükséges hozzá néhány programozási tétel: sorozatszámítás, megszámolás, valamint adatszerkezetként ideális egy kétdimenziós tömb. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az oktatas.hu-ról.
12. feladat
Egy kockával kétszer egymás után dobunk. Adja meg annak a valószínűségét, hogy a két dobott szám összege 7 lesz! Válaszát indokolja!
Matematikai megoldás
A feladat nagyon egyszerű. Két megoldást ismertet a javítási-értékelési útmutató:
- Összesen 6 * 6 = 36-féleképpen dobhatunk. Hat olyan dobáspár van, amelyben 7 az összeg: (1; 6), (2; 5), (3; 4), (4; 3), (5; 2) és (6; 1). A keresett valószínűség 6/36-od, vagyis egyhatod.
- Bármennyit is dobunk elsőre, ezt a második dobás egyféleképpen egészítheti ki 7-re. Így a második dobásnál a hat lehetséges értékből egy lesz számunkra kedvező. A keresett valószínűség egyhatod.
Közelítő megoldások szimulációval
Egy alkalom két kockadobást jelent egymás után. A dobások sorrendje nem számít (alkalmanként és összességében sem). Minél több alkalommal végezzük el a kockadobásokat, annál jobban megközelítjük a fenti valószínűséget (várható értéket, bővebben: nagy számok törvénye). Az egyhatod közelítő értéke a Java
double adattípusával 0.16666666666666666.
1. megoldás
Ha nem akarunk emlékezni a dobásokra, összegükre, csupán megszámolnánk, hogy hány olyan dobáspár van, amelyben 7 az összeg, akkor ehhez mindössze egy számláló ciklus kell, aminek a ciklusmagjában két véletlen kockadobás összegét előállítjuk és növelünk egy számlálót/gyűjtőt, ha az éppen 7. Az eredményt a számláló és a ciklus lépésszámának hányadosa adja meg. Például meghívhatjuk a metódust így:
kockadobas1(5000); és kaphatjuk eredményül ezt:
5000 alkalomból 7 összegként 836 alkalommal fordult elő. Valószínűség: 0.1672 . A metódus kivételt dob, ha értelmetlen a paramétere. Íme a metódus Java forráskódja:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
static void kockadobas1(int alkalomDb) { if(alkalomDb<=0) throw new IllegalArgumentException("Hiba: alkalomDb<=0"); int osszeg7db=0; for(int i=1; i<=alkalomDb; i++) { int dobas1=(int)(Math.random()*6+1); int dobas2=(int)(Math.random()*6+1); if(dobas1+dobas2==7) osszeg7db++; } System.out.println( alkalomDb+" alkalomból 7 összegként "+ osszeg7db+" alkalommal fordult elő. Valószínűség: "+ ((double)osszeg7db/alkalomDb)); } |
2. megoldás
Ha egy 13 elemű egész típusú tömböt használhatunk emlékezetként. Kezdetben 2-től 12-ig indexelve nullázzuk ki, így csoportos gyűjtést tudunk megvalósítani. A nullázás most inicializáló blokkal történt, mert nem sok eleme van a tömbnek (sok elemnél inkább használjunk erre ciklust). A tömb első két elemét nem használjuk semmire. Mi történik a ciklusban? Például dobas1=3 és dobas2=4 esetén a dobasDbTomb[7] elemét növeli (mindegy mi volt ott korábban, de inkrementálódjon). Most több adatot tárolunk, mint amiből megválaszolható a feladatban megfogalmazott konkrét kérdés, de ezt tekinthetjük strukturális tartaléknak.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
static void kockadobas2(int alkalomDb) { if(alkalomDb<=0) throw new IllegalArgumentException("Hiba: alkalomDb<=0"); int[] dobasDbTomb={-1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; for(int i=1; i<=alkalomDb; i++) { int dobas1=(int)(Math.random()*6+1); int dobas2=(int)(Math.random()*6+1); dobasDbTomb[dobas1+dobas2]++; } System.out.println( alkalomDb+" alkalomból 7 összegként "+ dobasDbTomb[7]+" alkalommal fordult elő. Valószínűség: "+ ((double)dobasDbTomb[7]/alkalomDb)); } |
Hasonló, egydimenziós tömbbel történő belső adattárolást megvalósító elosztott alkalmazásról blogoltunk már: Kockadobás kliens-szerver alkalmazás.
3. megoldás
Ez az igazi szimuláció, swing GUI grafikus környezetben, ahogyan az alábbi képernyőképen látható. A megvalósítás kétdimenziós tömböt használ adatszerkezetként. Álljon 7 sorból és 7 oszlopból és legyen
i a sor- és
j az oszlopindex. A tömb
[0][0]-dik elemét nem használjuk semmire. Az első oszlopába (
j=0 és
i>0) bekerülhetnek a dobókockán előforduló számok 1-től 6-ig. Hasonlóan az első sorba (
i=0 és
j>0) is. Ezek a dobott számok alapján indexek lesznek és az ábrán zöld hátterű cellákba kerültek. A tömb többi eleme kezdetben 0 (nulla), ezek az ábrán fehér hátterű cellák. A szürke hátterű cellák (mellékátló) esetén a dobott számok összege 7 és jól látszik, hogy ez hatféleképpen fordulhat elő a 36-féle eset közül. Például a 2. sor 5. oszlopában lévő szám mutatja, hogy a 10000 alkalomból 274-szer fordult elő az, hogy a dobáspár a (2; 5) lett. A tömb két indexe felcserélhető lenne, mert ez a mellékátlóban lévő számok összegét nem befolyásolja.
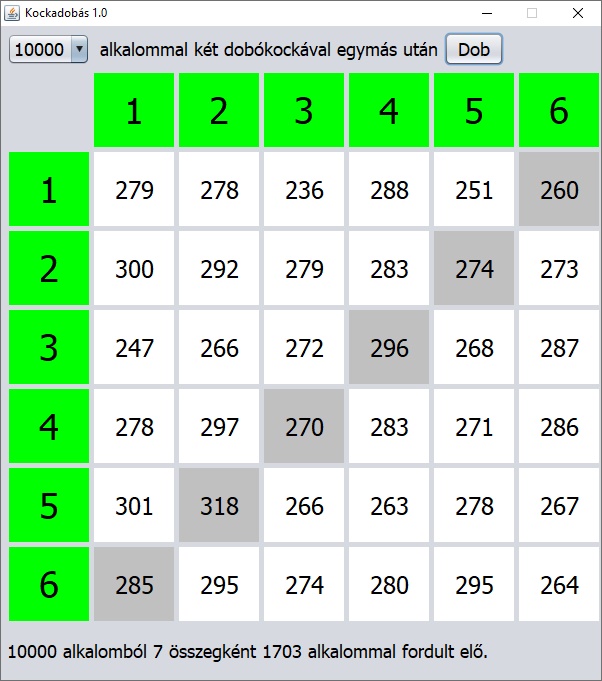
A programban kiválasztható néhány alkalomból amit szeretnénk, és a Dob nyomógombra kattintva indul el időzítővel a folyamat. Várakoztatás/menet közben piros színnel kiemelve látszik/megfigyelhető, hogy az éppen aktuális dobás hol növeli az értéket/előfordulást/darabszámot. A képernyőképen befejeződött állapot látható. Az eredményt a szürke cellákban lévő számok összegének és az alkalmak számának hányadosa adja meg. Ezt a háttérbeli kétdimenziós tömbben összesítéssel az alábbi Java forráskód-részlet adja meg:
|
1 2 3 4 5 |
int osszeg7db=0; for (int i = 1; i <= 6; i++) osszeg7db+=dobasTomb[i][7-i]; String eredmeny=alkalomDb+" alkalomból 7 összegként "+ osszeg7db+" alkalommal fordult elő."; |
Most lényegesen több adatot tárolunk, mint ami a konkrét válaszhoz kell, de cserébe jól érzékeltethető a csoportos gyűjtés/megszámolás működése. A program grafikus felhasználói felületének felépítését és az eseménykezelés megvalósítását most nem részletezzük.
Eszünkbe juthatna, hogy a program miért dob kétszer 1 és 6 közötti számot egymás után és ezt összegzi, amikor egyetlen 2 és 12 közötti dobással (véletlenszám generálással) megkaphatnánk a dobáspár összegét. Hiszen két db 1 és 6 közötti szám összege mindig 2 és 12 közötti szám. Jó lenne ez az ötlet/megvalósítás? Igen? Nem? Miért? A hozzászólásokhoz várjuk az indoklást.
Ajánljuk matematika érettségi feladat címkénket, mert a témában évről-évre blogolunk.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 17-28. óra: Objektumorientált programozás alkalmaira épülő 29-36. óra: Grafikus felhasználói felület alkalmaihoz kötődik.
Válasz a kérdésre:
Nem lenne jó, mert ha egyetlen 2 és 12 közötti dobással (véletlenszám generálással) állítanánk elő a dobáspár összegét, akkor a 11-féle lehetőség miatt egytizenegyed lenne az esélye egy összegnek. Mindegyikre közel azonos lenne a gyakoriság/előfordulás. Ez egyenletes eloszlás lenne és nem jönne ki, hogy két dobással a 7 a leggyakoribb összeg.
Orsi: hát ez gyorsan ment. 😉 Precíz indoklás, így van.