Out of her favour, where I am in love.
Alas, that love, whose view is muffled still,
Here's much to do with hate, but more with love.
Why, then, O brawling love! O loving hate!
This love feel I, that feel no love in this.
Why, such is love's transgression.
With more of thine: this love that thou hast shown
Love is a smoke raised with the fume of sighs;
Being purged, a fire sparkling in lovers' eyes;
Being vex'd a sea nourish'd with lovers' tears:
In sadness, cousin, I do love a woman.
A right good mark-man! And she's fair I love.
From love's weak childish bow she lives unharm'd.
She hath forsworn to love, and in that vow
widow of Vitravio; Signior Placentio and his lovely
One fairer than my love! the all-seeing sun
Under love's heavy burden do I sink.
Is love a tender thing? it is too rough,
Did my heart love till now? forswear it, sight!
It is my lady, O, it is my love!
O, that I were a glove upon that hand,
Call me but love, and I'll be new baptized;
With love's light wings did I o'er-perch these walls;
For stony limits cannot hold love out,
And what love can do that dares love attempt;
And but thou love me, let them find me here:
Than death prorogued, wanting of thy love.
By love, who first did prompt me to inquire;
If my heart's dear love--
The exchange of thy love's faithful vow for mine.
Wouldst thou withdraw it? for what purpose, love?
Love goes toward love, as schoolboys from
But love from love, toward school with heavy looks.
How silver-sweet sound lovers' tongues by night,
Then plainly know my heart's dear love is set
And bad'st me bury love.
I pray thee, chide not; she whom I love now
Doth grace for grace and love for love allow;
A gentleman, nurse, that loves to hear himself talk,
Then love-devouring death do what he dare;
Tybalt, the reason that I have to love thee
But love thee better than thou canst devise,
Till thou shalt know the reason of my love:
Wert thou as young as I, Juliet thy love,
My conceal'd lady to our cancell'd love?
No nightingale: look, love, what envious streaks
That may convey my greetings, love, to thee.
And trust me, love, in my eye so do you:
Ah me! how sweet is love itself possess'd,
When but love's shadows are so rich in joy!
By heaven, I love thee better than myself;
Call this a lightning? O my love! my wife!
Here's to my love!
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017


 Vajon hogyan kerül elő a Rómeó és Júlia az
Vajon hogyan kerül elő a Rómeó és Júlia az  A
A 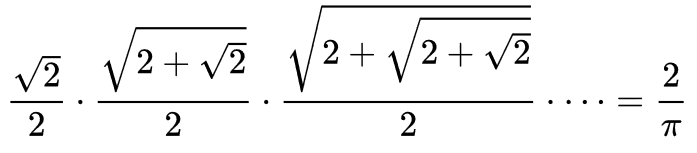
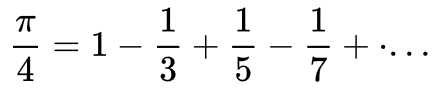
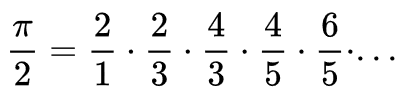
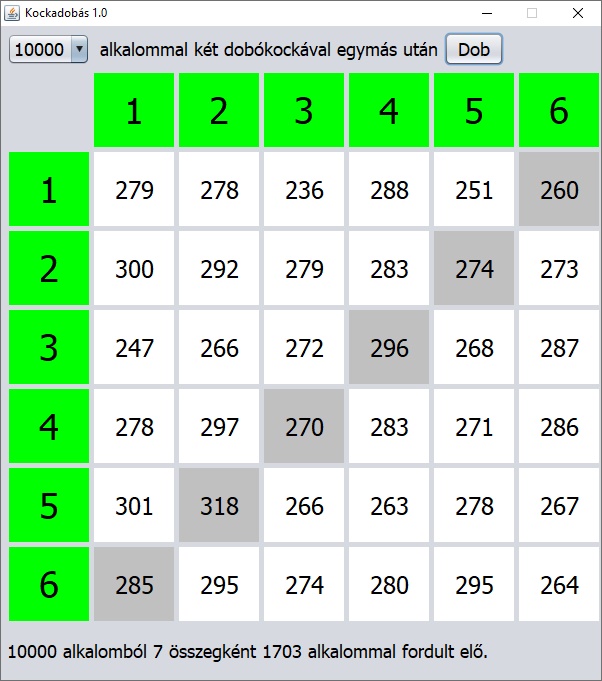
 A 2017-es középszintű matematika érettségi feladatsor 12. feladata inspirált egy Java program megírására. Szükséges hozzá néhány programozási tétel: sorozatszámítás, megszámolás, valamint adatszerkezetként ideális egy kétdimenziós tömb. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az
A 2017-es középszintű matematika érettségi feladatsor 12. feladata inspirált egy Java program megírására. Szükséges hozzá néhány programozási tétel: sorozatszámítás, megszámolás, valamint adatszerkezetként ideális egy kétdimenziós tömb. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az