CHOO + CHOO = TRAIN

2023. július 5.2017. február 5. Szerző: Kaczur Sándor

Most nem a híres kisvonatról van szó, hanem egy ismert kriptoaritmetikai feladványról. Ebben a feladattípusban egyszerű matematikai műveletek szerepelnek és a különböző betűk különböző számjegyeket jelölnek. Általában többféleképpen megoldhatók: intuíció, ötlet, módszeres próbálkozás, következtetés, kizárás vagy klasszikus behelyettesítés. Ha van megoldás és meg is találunk egyet, akkor a következő kérdés az, hogy van-e még, illetve összesen hány megoldás van?

Íme a feladat:

Érdemes minden megoldás során figyelembe venni a minden számjegyet 0-9-ig végigpróbáló lépések helyett legalább az alábbi öt feltételt:

C >= 5, hiszen CHOO olyan négyjegyű szám, aminek a kétszerese ötjegyű szám,
T = 1, mivel két négyjegyű szám összege 10000 < TRAIN < 20000 (ebben az esetben),
O >= 6, hiszen maradéknak képződnie kell, mert I és N különbözik,
2 <= N < I és
I >= 3 és szintén a maradékképződés miatt.

Esetleg még tovább gondolkodva, felfedezhetünk egyéb összefüggéseket, illetve kizárhatunk egyéb értékeket, így jelentősen csökkenthető egy-egy Java implementáció lépésszáma.

1. megoldás

Ez adatszerkezet nélküli megoldás, így eléggé összetett feltétellel valósul meg a művelet teljesülése (megfelelő helyiértékek használatával) és a különbözőségek vizsgálata.

public static void chooChooTrain1() {

for (int c = 5; c <= 9; c++)

for (int h = 0; h <= 9; h++)

for (int o = 6; o <= 9; o++)

for (int r = 0; r <= 9; r++)

for (int a = 0; a <= 9; a++)

for (int i = 3; i <= 9; i++)

for (int n = 2; n < i; n++)

if((1000*c+100*h+10*o+o)*2 == 10000+1000*r+100*a+10*i+n &&

c!=h && c!=o && c!=1 && c!=r && c!=a && c!=i && c!=n &&

h!=o && h!=1 && h!=r && h!=a && h!=i && h!=n &&

o!=1 && o!=r && o!=a && o!=i && o!=n &&

r!=1 && r!=a && r!=i && r!=n &&

a!=1 && a!=i && a!=n &&

i!=1 && i!=n &&

n!=1)

System.out.println(

" "+c+h+o+o+"\n+ "+c+h+o+o+"\n------\n "+1+r+a+i+n+"\n");

}

2. megoldás

Itt az ellenőrzési feltétel egyszerűbb, mert a különbözőség/egyediség tesztelését áthárítottam a halmazszerűen működő HashSet generikus kollekcióra, építve annak beépített képességére.

public static void chooChooTrain2() {

HashSet<Integer> hs=new HashSet<>();

for (int c = 5; c <= 9; c++)

for (int h = 0; h <= 9; h++)

for (int o = 6; o <= 9; o++)

for (int r = 0; r <= 9; r++)

for (int a = 0; a <= 9; a++)

for (int i = 3; i <= 9; i++)

for (int n = 2; n < i; n++) {

hs.add(c); hs.add(h); hs.add(o);

hs.add(1); hs.add(r); hs.add(a); hs.add(i); hs.add(n);

if(hs.size()==8 &&

(1000*c+100*h+10*o+o)*2 == 10000+1000*r+100*a+10*i+n)

System.out.println(

" "+c+h+o+o+"\n+ "+c+h+o+o+"\n------\n "+1+r+a+i+n+"\n");

hs.clear();

}

Mit gondolsz, melyik megoldás hajtódik végre gyorsabban? Miért?

Mivel a két megoldásnál a ciklusok szervezése megegyezik, így a használt adatszerkezet dönt (hiszen annak konstrukciós és szelekciós, azaz karbantartási műveletei vannak). Az 1. megoldás a gyorsabb, mert nem használ adatszerkezetet. A 2. megoldás lényegesen lassabban fut, mert a generikus kollekció műveletei miatt az automatikus szemétgyűjtő tevékenység erősen igénybe vett. A különbség nagyságrendileg 15-szörös.

A feladatnak két megoldása van: 5466 + 5466 = 10932 és 5488 + 5488 = 10976.

A bejegyzéshez tartozó teljes – időméréssel kiegészített – forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

Akinek kedve támadt, lásson hozzá hasonló feladatokhoz:

SEND + MORE = MONEY
6 * KAYAK = SPORT
2 * MOST = TOKYO
CROSS + ROADS = DANGER
FORTY + TEN + TEN = SIXTY
mathsisfun.com – Algebra Puzzles
cryptarithms.awardspace.us – Crack-a-Puzzle Online – Puzzles Menu
www.campusgate.co.in – Cryptoarithmetic problem with explanation

A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió alkalomhoz, illetve a 21-24. óra: Objektumorientált programozás, 2. rész alkalomhoz kötődik.

Ajánljuk a Java SE szoftverfejlesztő tanfolyam kategóriából

Doktoranduszok programoznak – újratöltve

Nemzetközi Pi nap

Hello World! másképpen

Kígyókocka grafikus felületen

Rácsrejtjelezés

Táblázatos hőtérkép készítése

“CHOO + CHOO = TRAIN” bejegyzéshez 13 hozzászólás

Balogh Péter

2018. május 25. - 00:16

A SEND+MORE=MONEY kézi megoldását láthatjuk a videóban lépésenként:
https://www.youtube.com/watch?v=kKF-qBaGgAY
Válasz
Balogh Péter

2019. február 3. - 09:56

Ajánljuk rendezvényeinket, ahol időről-időre tartunk élményszerű foglalkozásokat, válogatva a logikus gondolkodásra nevelés feladatgyűjteményünkből.
Válasz
Balogh Péter

2020. február 9. - 08:59

Itt egy másik hasonló gondolkodtató feladvány:

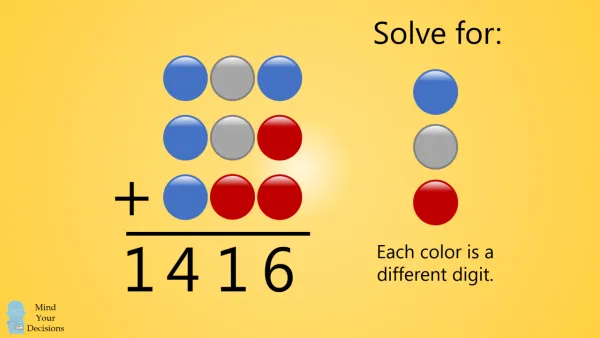
Az alábbi weboldalon találtam, ahol van hozzá szöveges magyarázat, ppt és videó is:
https://mindyourdecisions.com/blog/2020/01/27/solve-for-3-digits-belgian-olympiad/
Válasz
- E. István
  
  2020. március 2. - 09:16
  
  Én is találtam egy jót:
  
  Válasz
Kiss Balázs

2020. augusztus 17. - 22:03

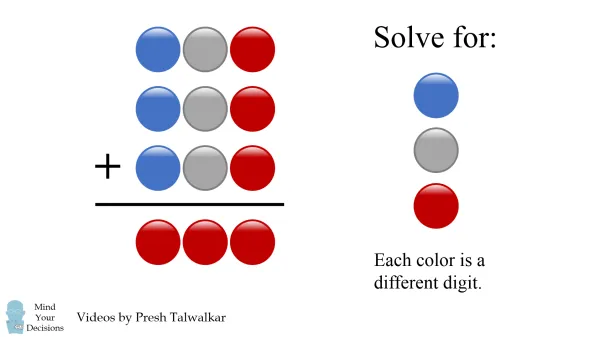
A népszerű gyermekdal (YT videó) 🙂
Train Song: Choo Choo Train for Children, Kids, Babies and Toddlers | Counting Song | Miss Patty
Válasz
Kaczur Sándor

2021. április 4. - 11:15
Íme néhány nehezebb példa a kihívást keresőknek. Ezeket már másképpen érdemes/hatékony megoldani:
- AN + ACCELERATING + INFERENTIAL + ENGINEERING + TALE + ELITE + GRANT + FEE + ET + CETERA = ARTIFICIAL + INTELLIGENCE
- NIIHAU ± KAUAI ± OAHU ± MOLOKAI ± LANAI ± MAUI ± HAWAII = 0
- PI * R * R = AREA
- NORTH / SOUTH = EAST / WEST
Nem csak egy konkrét példa megoldásának szintjén lehet gondolkodni, így aki még kitartóbb általánosabban is lehet: keresse meg az összes n₁ + ... + n_t = n'₁ + ... + n'_t' alakú egyenletet úgy, hogy angolul mind matematikailag, mind pedig alfametikailag igazak legyenek, ha minden változó 20-nál kisebb különböző pozitív egész. Például:
- TWELVE + NINE + TWO = ELEVEN + SEVEN + FIVE
Forrás: D. E. Knuth: A számítógép-programozás művészete, 4. kötet, 2. rész, Permutációk és n-esek előállítása, AnTonCom Infokommunikációs Kft., Budapest, 2008, ISBN 987-963-87947-1-0
Válasz

Úgy érzem, hogy megértettem a rekurziót az ILIAS-os példák alapján és próbálkoztam ezzel a feladattal. Tehát íme a CHOO + CHOO = TRAIN rekurzívan:

public static void chooChooTrain3(String s) {

if(s.length()==8) {

int c=s.charAt(0)-'0', h=s.charAt(1)-'0', o=s.charAt(2)-'0',

t=s.charAt(3)-'0', r=s.charAt(4)-'0', a=s.charAt(5)-'0',

i=s.charAt(6)-'0', n=s.charAt(7)-'0';

if(c!=0 && t!=0 &&

(1000*c+100*h+10*o+o)*2 == 10000*t+1000*r+100*a+10*i+n)

System.out.println(

" "+c+h+o+o+"\n+ "+c+h+o+o+"\n------\n "+t+r+a+i+n+"\n");

}

else

for(int i=0; i<=9; i++)

if(!s.contains(""+i))

chooChooTrain3(s+i);

}

Válasz

Látszik, hogy alaposan átgondoltad és megértetted a rekurziót Anett. A szöveg jelenti az emlékezetet a programodban. A karakterek számmá átalakításához a karakterkódok különbségeit használtad. Én is továbbgondoltam a megoldásodat és kicseréltem ezt csomagolóosztály konvertáló függvényére úgy, hogy a számjegyeket ; választja el egymástól:

public static void chooChooTrain4(String s) {

String[] d=s.split(";");

if(d.length==9) {

int c=Integer.parseInt(d[1]), h=Integer.parseInt(d[2]),

o=Integer.parseInt(d[3]), t=Integer.parseInt(d[4]),

r=Integer.parseInt(d[5]), a=Integer.parseInt(d[6]),

i=Integer.parseInt(d[7]), n=Integer.parseInt(d[8]);

if(c!=0 && t!=0 &&

(1000*c+100*h+10*o+o)*2 == 10000*t+1000*r+100*a+10*i+n)

System.out.println(

" "+c+h+o+o+"\n+ "+c+h+o+o+"\n------\n "+t+r+a+i+n+"\n");

}

else

for(int i=0; i<=9; i++)

if(!s.contains(""+i))

chooChooTrain4(s+";"+i);

}

Nem mértem, hogy melyikünk megoldása hatékonyabb, csak egy alternatívát szerettem volna mutatni. A rekurzió általában mindig lassabban működik az iterációhoz képest. Persze a használt adatszerkezet karbantartó műveleteinek igényeire is tekintettel kell lenni. Örülök, hogy inspirált a feladat.

Válasz

Kriszta

2023. január 3. - 10:01

Gratulálok Anett, hogy már itt tartasz. Én ezeket még nem ugrottam meg, de már kitaláltam, hogy a két alábbi c miért egyezik meg:

c=s.charAt(0)-'0';

c=Integer.parseInt(s.split(";")[1]);

😉
Válasz
- Kaczur Sándor
  
  2023. január 3. - 10:17
  
  Ez is rendben van Kriszta, hiszen fontos és szükséges lépés az odavezető úton.
  Válasz
K. Anett

2023. január 3. - 10:04

Köszönöm Sándor. Kipróbáltam az ILIAS-ban lévő Unit tesztes időmérő tesztkörnyezettel és ezeket kaptam:
1. megoldás végrehajtási ideje: 9 ms
2. megoldás végrehajtási ideje: 129 ms
3. megoldás végrehajtási ideje: 395 ms
4. megoldás végrehajtási ideje: 2361 ms
Szóval a rekurzió fejben nagyon szép, de a gyakorlatban nem annyira.
Válasz
- Kaczur Sándor
  
  2023. január 3. - 10:15
  
  Köszönöm Anett. Örülök, hogy ehhez összeraktad fejben az öröklődéssel való testre szabást is, ami kellett a teszteléshez ebben a környezetben.
  Válasz

Kiss Balázs

2023. január 3. - 10:27

Nohát, micsoda aktivitás van itt újév alkalmából. 🙂 Anett, Kriszta: igazán motiváltak vagytok, szuper!
Válasz

1. megoldás

2. megoldás

Ajánljuk a Java SE szoftverfejlesztő tanfolyam kategóriából

“CHOO + CHOO = TRAIN” bejegyzéshez 13 hozzászólás

Szólj hozzá! Válasz megszakítása