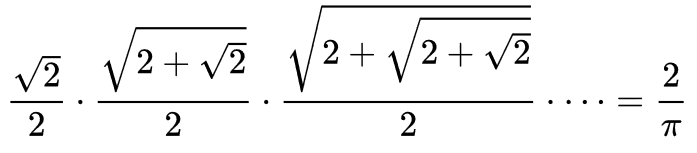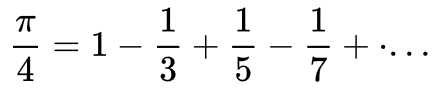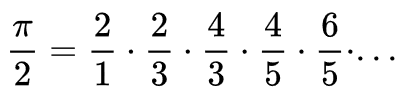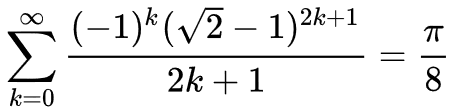2 blog bejegyzésnél szerepel:
23 db hozzá kapcsolódó címke:
2018 (24), 2024 (20), algoritmus (33), becslés (6), évforduló (24), fájlkezelés (29), grafika (30), grafikus felhasználói felület (44), hatékonyság (30), Java forráskód (70), közelítés (3), lépésszám (10), matematika (34), metódus (33), naptár (26), objektumorientált programozás (94), Pi nap (2), programozás (116), rajzolás (17), szakmai modul (104), többféle megoldás összehasonlítása (42), tömb (18), ünnepnap (13)
A nemzetközi Pi nap alkalmából (március 14) Java programmal grafikusan ábrázoljuk a π számjegyeit. Kiindulunk egy négyzet alakú grafikus felület középpontjából. Ezt tekintjük origónak. Sorra vesszük a π első néhány számjegyét: 100, 1000, 10000 paraméterezhető módon. Minden számjegyet egy rövid szakasszal ábrázolunk. A szakaszok egymást követik. Az előző végpontja megegyezik a következő kezdőpontjával. A rajzolás elejét és végét kör jelzi.
Az alábbi szabály alapján döntjük el, hogy a π előforduló számjegyei esetén melyik irányba és milyen színnel rajzolunk szakaszt:
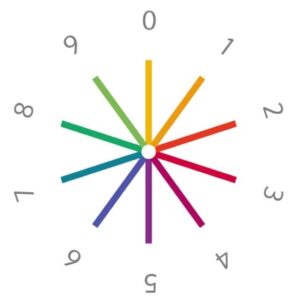
A π első 100000 db számjegyét tároljuk egy szövegfájlban. Ömlesztve, sortörés, tizedesvessző nélkül. Így a π első 30 számjegye: 314159265358979323846264338327. A szövegfájl helyét a String PI_FILE konstans jegyzi meg. A paraméternek megfelelően ebből vesszük az első N db számjegyet. Ezt a Java program beolvassa egy String típusú pi szövegobjektumba. A számjegyek összetartozó adatait egy Digit osztály rendeli egymáshoz. Ennek három adattagja van: melyik számjegy: int digit, melyik irányba kell szakaszt rajzolni java.awt.Point direction, milyen színnel kell szakaszt rajzolni java.awt.Color color. A tízféle színt egy konstans tömb tárolja: Color[] COLORS.
A π tízféle számjegyéből az alábbi forráskód-részlettel létrejön egy tömb adatszerkezet: Digit[] digits. A koordináták/vektorok kiszámítása követi az analóg óra számlapjának 36 fokonként való felosztását.
|
1 2 3 4 5 6 7 |
for(int i=0; i<10; i++) { Point p=new Point( (int)(Math.cos(Math.toRadians(i*36-90))*LINE_LENGTH), (int)(-Math.sin(Math.toRadians(i*36-90))*LINE_LENGTH) ); digits[i]=new Digit(i, p, COLORS[i]); } |
A rajzoláshoz szükséges még néhány konstans: milyen vastag vonalat kell rajzolni: double PEN_RADIUS, mekkora átmérőjű kör jelzi a rajzolás kezdő- és végpontját: double POINT_RADIUS, milyen hosszú vonalat kell rajzolni: int LINE_LENGTH, a rajzterületet mekkorára kell méretezni/skálázni: int SCALE.
Mindezek alapján az alábbi forráskód-részlet vizualizálja a π számjegyeit:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
private void piDraw() { StdDraw.setScale(-SCALE, SCALE); StdDraw.setPenRadius(PEN_RADIUS); Point p1=new Point(0, 0); StdDraw.setPenColor(digits[3-1].getColor()); StdDraw.circle(p1.x, p1.y, POINT_RADIUS); for(int i=0; i<PI.length(); i++) { int digit=Integer.parseInt(""+PI.charAt(i)); Point p2=new Point( p1.x+digits[digit].getDirection().x, p1.y+digits[digit].getDirection().y); StdDraw.setPenColor(digits[digit].getColor()); StdDraw.line(p1.x, p1.y, p2.x, p2.y); p1=p2; } StdDraw.circle(p1.x, p1.y, POINT_RADIUS); } |
Eredményül ezek az ábrák készíthetők el:
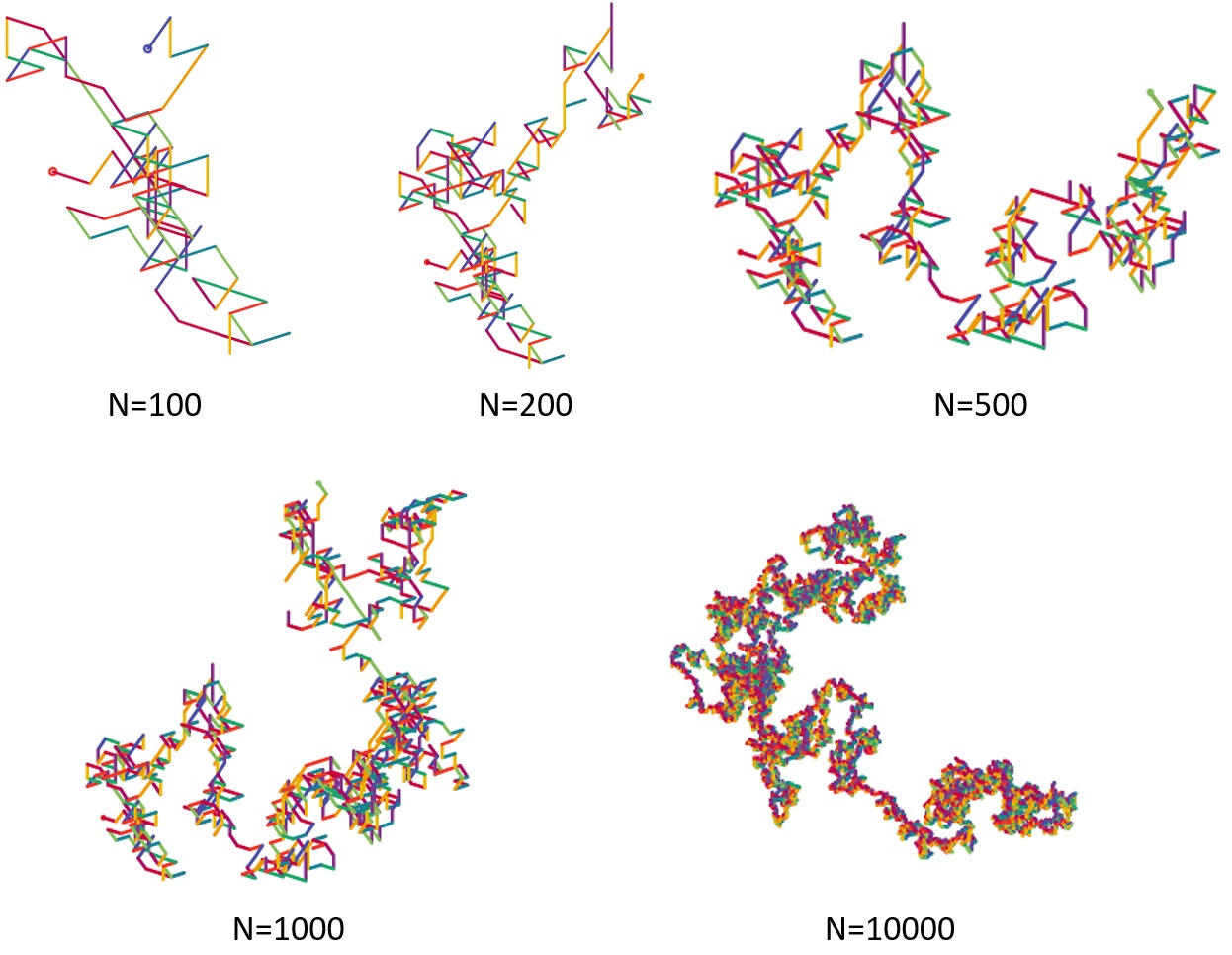
A rajzoláshoz felhasználtuk az StdDraw osztályt, amely ennek a tankönyvnek a példatárából származik: Robert Sedgewick, Kevin Wayne: Computer Science: An Interdisciplinary Approach, 1st edition, Princeton University, Addison-Wesley Professional, 2016, ISBN 978-0134076423. Az osztály metódusaival könnyen beállítható a nézőpont, a vízszintes/függőleges skála, a rajzoláshoz használt toll mérete/színe és a grafikai primitívek közül csak a kör és szakasz ábrázolása szükséges.
Korábban is megemlékeztünk néhány közelítő algoritmus – Viète-féle sor, Leibniz-féle sor, Wallis-formula, Csebisev-sor – implementálásával erről az ünnepnapról: Nemzetközi Pi nap. Ajánljuk korábbi blog bejegyzéseinket rajzolás, animáció, grafika címkékkel, illetve ASCII művészet Java-ban.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 5-8. óra: Vezérlési szerkezetek, 13-16. óra: Tömbök, 17-28. óra: Objektumorientált programozás, 29-36. óra: Grafikus felhasználói felület, 37-44. óra: Fájlkezelés alkalmaihoz kötődik.
A Pi-t (π) mindenki ismeri. Talán sokaknak kedvenc története is van a π-vel kapcsolatosan, amelyet iskolában vagy utazásai alatt szerzett. A π Euklidesz geometriájában a kör kerületének és átmérőjének arányát jelöli. A π irracionális szám, azaz végtelen, nem szakaszos tizedestört; másképpen számjegyei között nincs ismétlődés. A π értékével a hétköznapokban 3,14-dal szokás számolni, de a tudomány területén ennél sokkal pontosabb közelítést szokás alkalmazni. A π közelítése az informatikának köszönhetően akár több millió tizedesjegyig is lehetséges (például: S. Memphill: Pi to 1,000,000 places).
A nemzetközi Pi nap alkalmából (március 14) megvalósítottunk néhány – végtelen összeggel és szorzattal – π közelítésre való képletet, algoritmust Java nyelven.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
private static void megold1() { //Viète-féle sor double p=1, pi=1; for(int i=11; i>1; i--) { p=2; for(int j=1; j<i; j++) p=2+Math.sqrt(p); p=Math.sqrt(p); pi=pi*p/2; } pi*=Math.sqrt(2)/2; pi=2/pi; System.out.println(pi); } |
A módszer néhány eredménye: i=5 esetén 3.140331156954752 (2 tizedesjegyre pontos), i=10-nél 3.1415914215112 (5 tizedesjegyre pontos), i=11 esetén 3.1415923455701176 (6 tizedesjegyre pontos).
|
1 2 3 4 5 6 7 |
public static void megold2() { //Leibniz-féle sor double s=0; for(int i=0; i<=2500; i++) s+=Math.pow(-1, i)/(2*i+1); double pi=s*4; System.out.println(pi); } |
A módszer néhány eredménye: a 24. lépéstől stabil 1 tizedesjegyre, a 626. lépéstől stabil 2. tizedesjegyre, a 2453. lépéstől stabil 3 tizedesjegyre (hiszen alternál).
|
1 2 3 4 5 6 7 |
public static void megold3() { //Wallis-formula double p=1; for(int i=2; i<=17000; i+=2) p*=(1.0*i/(i-1)*(1.0*i/(i+1))); double pi=p*2; System.out.println(pi); } |
A módszer néhány eredménye: A 38. lépéstől 1, a 986. lépéstől 2, a 2650. lépéstől 3, a 16954. lépéstől már 4 tizedesjegyre pontos.
|
1 2 3 4 5 6 7 |
private static void megold8() { //Csebisev-sor, V1 double s=0; for(int k=0; k<=20; k++) s+=(Math.pow(-1, k)*Math.pow(Math.sqrt(2)-1, 2*k+1))/(2*k+1); double pi=s*8; System.out.println(pi); } |
A módszer k=10-re már 8 tizedesjegyig pontos.
A bejegyzéshez tartozó teljes forráskódot – további 8 közelítő módszer implementációjával együtt – ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 5-8. óra: Vezérlési szerkezetek alkalmához kötődik.