lépésszám - címke - it-tanfolyam.hu

Egy matematika érettségi feladat megoldása programozással 2021

2023. január 3.2021. május 4. Szerző: Kaczur Sándor

A 2021-es középszintű matematika érettségi feladatsor 12. feladata inspirált arra, hogy a programozás eszköztárával oldjuk meg ezt a feladatot. Szükséges hozzá néhány programozási tétel: sorozatszámítás, eldöntés, megszámolás, kiválogatás. Többféle megoldás/megközelítés is előkerül. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az oktatas.hu-ról.

12. feladat

A háromjegyű pozitív egész számok közül véletlenszerűen kiválasztunk egyet. Mennyi annak a valószínűsége, hogy a kiválasztott szám számjegyei különbözők? Megoldását részletezze!

1. megoldás

static void feladat12Megoldas1() {

int db=0;

for(int szazas=1; szazas<=9; szazas++)

for(int tizes=0; tizes<=9; tizes++)

for(int egyes=0; egyes<=9; egyes++)

if(szazas!=tizes && tizes!=egyes && szazas!=egyes)

db++;

System.out.println("1. megoldás: "+db/900.0);

}

Az 1. megoldás egymásba ágyazott ciklusokkal behelyettesíti a szóba jöhető 900 db háromjegyű szám számjegyeit. A feltétel 648 esetben teljesül. Három számjegy azonosságát két részfeltétel és kapcsolatával eldönthetnénk a trichotómia miatt. Három számjegy különbözőségéhez három részfeltétel és kapcsolatából áll össze a feltétel. A válasz a kedvező és összes eset aránya/hányadosa, azaz 0,72. Másképpen 648 db szám a 900 db háromjegyű szám közül. A megoldás lépésszáma 900.

2. megoldás

static void feladat12Megoldas2() {

int db=0;

for(int szazas=1; szazas<=9; szazas++)

for(int tizes=0; tizes<=9; tizes++)

if(szazas!=tizes)

for(int egyes=0; egyes<=9; egyes++)

if(tizes!=egyes && szazas!=egyes)

db++;

System.out.println("2. megoldás: "+db/900.0);

}

Az egymásba ágyazott ciklusok lépésszáma összeszorzódik. A legbelső ciklus az előtte lévő feltételtől függően kevesebbszer is végrehajtódhat, hiszen a százas és tízes helyiértéken lévő számjegyek egyezése esetén nincs értelme az egyes helyiértéken lévő számjegy vizsgálatának. Így a 2. megoldás lépésszáma 810, azaz 10%-kal kevesebb. Ez a három részből álló feltétel két részre bontásával érhető el.

3. megoldás

static void feladat12Megoldas3() {

int db=0;

for(int i=100; i<=999; i++) {

int szazas=i/100;

int tizes=i%100/10;

int egyes=i%100%10;

if(szazas!=tizes && tizes!=egyes && szazas!=egyes)

db++;

}

System.out.println("3. megoldás: "+db/900.0);

}

A 3. megoldásban egyetlen ciklus végzi a vizsgálatot, a megszámolást. A ciklusváltozó már nem számjegy, hanem maga a háromjegyű szám, amiről döntést kell hozni: különbözik-e mindegyik számjegye vagy sem. Három beszédes nevű segédváltozó segít értelmezni a Java forráskódot. Ezek az egész osztás és a maradékos osztás műveleteivel állíthatók elő.

4. megoldás

static boolean kulonbozoSzamjegyek(int i) {

int szazas=i/100;

int tizes=i%100/10;

if(szazas==tizes)

return false;

int egyes=i%100%10;

if(tizes==egyes || szazas==egyes)

return false;

return true;

}

static void feladat12Megoldas4() {

int db=0;

for(int i=100; i<=999; i++)

if(kulonbozoSzamjegyek(i))

db++;

System.out.println("4. megoldás: "+db/900.0);

}

A 4. megoldás logikai visszatérési értékű segédfüggvényt alkalmaz. Ez egy menekülőutas megoldás. Ha kizáró feltétel szerint már döntést tudunk hozni (például megegyezik a százas és a tízes helyiértéken lévő számjegy), akkor hamis értékkel menekülünk. Egyébként ág nélkül ezután következhet az egyes helyiértéken lévő számjegy összehasonlítása a többivel. A második feltétel az eddigiekhez képest tagadott, mert a menekülés a cél. Ha nincs menekülés amiatt, hogy volt két megegyező számjegy, akkor – a feltételek egymásra épülése miatt – nincs más hátra, mint igaz értékkel visszatérni (ami azt jelenti, hogy nem volt egyezés, azaz minden számjegy különbözött).

5. megoldás

static long kulonbozoSzamjegyDb(int i) {

return IntStream.of(i/100, i%100/10, i%100%10).distinct().count();

}

static void feladat12Megoldas5() {

int db=0;

for(int i=100; i<=999; i++)

if(kulonbozoSzamjegyDb(i)==3)

db++;

System.out.println("5. megoldás: "+db/900.0);

}

Az 5. megoldás segédfüggvénye a háromjegyű szám esetén a különböző számjegyek darabszámával tér vissza. A röptében előállított százaz, tízes, egyes helyiértékeken lévő számjegyekből folyam adatszerkezet készül, aminek feldolgozását a Stream API műveletei (egyediesítő, megszámoló) végzik el. Ezt a vezérlő ciklusban hárommal összehasonlítva léptethető a megszámolást megvalósító változó, hiszen ha teljesül a feltétel, akkor eggyel több megfelelő szám van, mint előtte volt.

6. megoldás

static void feladat12Megoldas6() {

int db=0;

for(int i=100; i<=999; i++) {

int szazas=i/100;

int tizes=i%100/10;

int egyes=i%100%10;

if(szazas==tizes || tizes==egyes || szazas==egyes)

db++;

}

System.out.println("6. megoldás: "+(900-db)/900.0);

}

Az 6. megoldás újra másképpen közelít. Ha könnyebbnek tűnik az a feltétel, hogy mikor nem jó (kedvezőtlen) nekünk egy szám, akkor beépíthetjük ezt is. Megszámoljuk azokat a háromjegyű számokat, amelyeknél egy vagy két számjegy azonos, majd ez kivonjuk a háromjegyű számok darabszámából.

7. megoldás

static void feladat12Megoldas7() {

long db=IntStream.range(100, 1000).

filter(i -> IntStream.of(i/100, i%100/10, i%100%10).

distinct().count()==3).count();

System.out.println("7. megoldás: "+db/900.0);

}

A 7. megoldás már mindent folyamokkal old meg, azok képességeire építve. Az összes háromjegyű számot előállítja, majd rajtuk kiválogatás programozási tételt (szűrőt) használ (az 5. megoldás segédfüggvényére építve), végül a folyamban maradó számokat megszámolja. Ez a megoldás már olyan haladóknak való, akik magabiztosan építik össze a Stream API műveleteit és a lambda kifejezéseket. Mindent egyben. Persze hol itt a hatékonyság? Hozzászólásokban megbeszélhetjük.

8. megoldás

static void feladat12Megoldas8() {

long db=IntStream.range(100, 1000).

filter(i -> !(i/100==i%100/10 && i%100/10==i%100%10)). //1. szűrő

filter(i -> !(i/100==i%100/10)). //2. szűrő

filter(i -> !(i%100/10==i%100%10)). //3. szűrő

filter(i -> !(i/100==i%100%10)). //4. szűrő

count();

System.out.println("8. megoldás: "+db/900.0);

}

A 8. megoldás szintén folyam adatszerkezettel működik, de négy egymást követő lépésben végez szűrést (kiválogatást). A 900 db háromjegyű számból indulunk ki. Az 1. szűrő kihagyja a 9 db AAA számot, amelyek számjegyei azonosak és így marad utána 891 db szám. A 2. szűrő után marad 810 db szám, mert kimarad az a 81 db AAB alakú szám (ahol a százas és tízes helyiértéken lévő számjegyek megegyeznek) az összesen 90 db-ból, ami még a folyamban maradt az 1. szűrő után. A 3. szűrő kihagy 81 db ABB alakú számot és meghagy 729 db számot. A 4. szűrő kihagy 80 db ABA alakú számot és meghagy 648 db ABC alakú számot.

A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

Ajánljuk matematika érettségi feladat címkénket, mert a témában évről-évre blogolunk.

A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 5-8. óra: Vezérlési szerkezetek, 13-16. óra: Tömbök, valamint 21-24. óra: Objektumorientált programozás, 2. és 3. rész alkalmaihoz kötődik.

Dr. Sheldon Cooper szólánc játéka

2022. július 8.2020. április 1. Szerző: Kaczur Sándor

Dr. Sheldon Cooper karakterét nem kell bemutatni. Az Agymenők (The Big Bang Theory) című sorozat 2. évad 5. epizódjának címe A vitatkozás nagymestere (The Euclid Alternative). Nagyon találó az epizód címe magyarul. Miközben Penny reggel Sheldont munkába viszi, Sheldon az autóban kémiai elemek nevéből álló szólánc játékával különösen Penny agyára megy (pedig a játékot Penny nyeri 😀):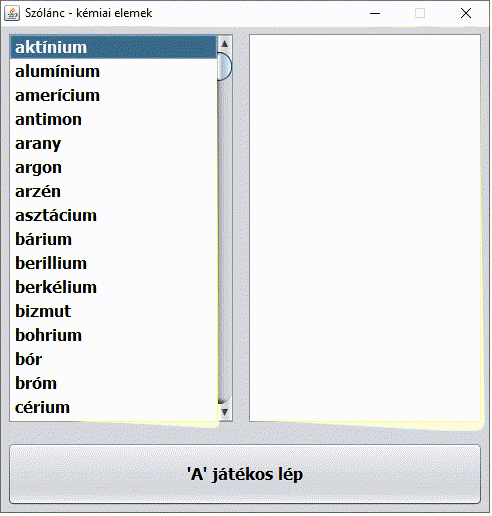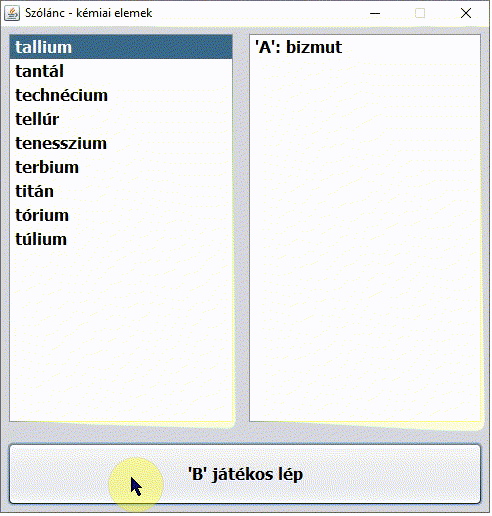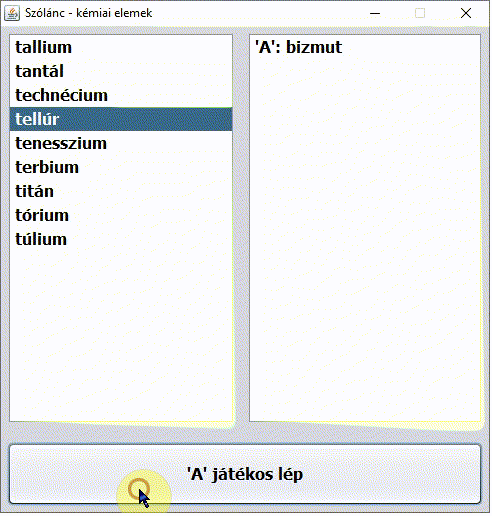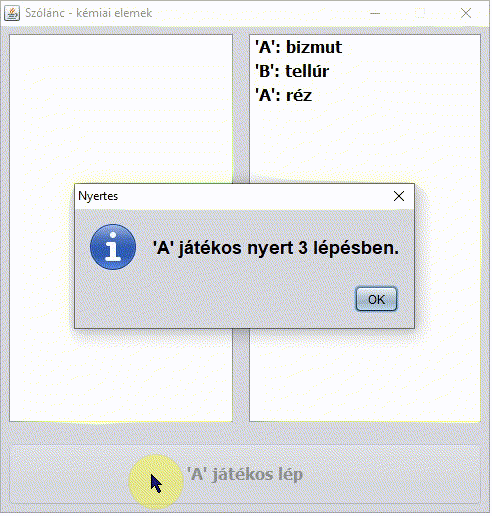

A játék során Sheldon az alábbi kémiai elemeket mondja:

magyar nyelven: Hélium ↦ Mangán ↦ Neptúnium ↦ Magnézium ↦ Molibdén ↦ Nitrogén ↦ Nobélium ↦ Mendelévium
angol nyelven: Helium ↦ Mercury ↦ Ytterbium ↦ Molybdenum ↦ Magnesium ↦ Manganese ↦ Europium ↦ Mendelevium

Támogassuk meg ezt a játékot! Készítsünk olyan programot Java nyelven, ami segít(ene) felkészülni Sheldon szólánc játékára!

A szükséges lépések áttekintése

Gyűjtsük össze a kémiai elemek nevét magyar nyelven a Wikipédia – Kémiai elemek listája szócikkéből és rendezzük ábécé sorrendbe!
Építsük be az elemlistát a program adatmodelljébe!
Indítsuk el a lépésszámláló nulláról! Ha a lépésszámláló páros, akkor az ’A’ játékos, egyébként a ’B’ játékos lép.
Készítsük elő a játékmenet tárolására alkalmas adatszerkezetet, szöveget, listát!
Kezdetben kínáljuk fel a teljes elemlistát úgy, hogy mindig egy és csak egy legyen belőle kiválasztható!
A kiválasztást követően tároljuk el a játékmenetben az elemet, töröljük ezt az elemlistából, majd kínáljuk fel azoknak az elemeknek a listáját, amelyek kezdőbetűje megegyezik az előzőleg kiválasztott elem utolsó betűjével és növeljük meg a lépésszámlálót!
Amíg a felkínálható elemek listája nem üres, addig az előző lépést ismételjük meg!
A játék végén az nyert, aki a játékmenet utolsó elemét választotta ki. Írjuk ki a nevét és a lépésszámot!

A grafikus felületű megvalósítás képernyőképe rövid játékmenettel

Ötletek a megvalósításra és a továbbfejlesztésre

A program Java nyelven konzolos menükezeléssel, asztali alkalmazásként swing-esen többféle GUI komponens használatával és eseménykezeléssel, böngészőben futó JSP webalkalmazásként többféle űrlapmezővel, illetve HTML+CSS+JavaScript alapon is implementálható.
A kémiai elemek listája lecserélhető az angol nevekre. Ekkor figyeljünk arra, hogy a kis- és nagybetűket ne különböztessük meg az utolsó-első betű párosítása során.
Lehet a játék bármikor megszakítható, illetve a vége után újrakezdhető.
A program mérhetné a játék során az eltelt időt.
A program lehetne peer-to-peer vagy szerver-kliens elosztott és megvalósíthatna hálózatos kommunikációt.
A program mobil alkalmazásként is implementálható.

A bejegyzéshez tartozó teljes forráskódot – többféle változatban is – ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

Többféleképpen is hozzájuthatunk az adatokhoz attól függően, hogy milyen előismeretekkel rendelkezünk a különböző tanfolyamainkon:

A Java SE szoftverfejlesztő tanfolyamon dolgozhatunk szövegtömbbel, generikus kollekcióval (listával/halmazzal), konzolos és swing-es változatot is készíthetünk. Ehhez a feladathoz objektumorientált alapok mindenképpen szükségesek. Kézzel előállított szövegfájlból olvasva (mentve a Wikipédia oldaláról a táblázatot) hozzájuthatunk a kémiai elemek nevéhez, amihez kivételkezelés is szükséges.
A Java EE szoftverfejlesztő tanfolyamon megvalósítható, hogy a program kivételkezeléssel hálózati kapcsolatot épít, majd közvetlenül olvassa és/vagy menti a Wikipédia HTML tartalmából a kémiai elemek nevét szövegfájlba vagy generikus kollekcióba, amivel a feladat visszavezethető az SE szemléletű megközelítésre. Böngészőben futó JSP és/vagy Servlet technológiára építő webalkalmazásként is megvalósítható a feladat.

Barátságos számok

2023. január 3.2018. július 19. Szerző: Balogh Péter

Azokat a számpárokat, amelyekre igaz, hogy az egyik szám önmagánál kisebb osztóinak összege megegyezik a másik számmal és fordítva, külön-külön barátságos számoknak, együtt barátságos számpárnak hívjuk.

Másképpen: legyen d(n) az n természetes szám önmagánál kisebb osztóinak összege. Ha d(a)=b és d(b)=a, ahol a≠b, akkor a és b barátságos számpár.

Például: (220; 284), hiszen a 220 önmagánál kisebb osztói: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 és ezek összege 284, illetve 284 önmagánál kisebb osztói: 1, 2, 4, 71, 142 és ezek összege 220.

Írjunk Java programot, amely kiírja az 1-10000 zárt intervallumban található barátságos számpárokat!

1. megoldás

A baratsagosSzamparok1() eljárás ciklusai a brute force módszer szerint behelyesítik az összes lehetséges számot. Minimális lépésszám csökkentésre adódik lehetőség, hiszen a belső ciklus j változója i+1-ről indítható (így a megtalált számpárok nem íródnak ki fordítva is, mert teljesül, hogy i<j).

Az osztokOsszege1(n) függvény is minden lehetséges osztót figyelembe vesz 1-től n-1-ig.

private static int osztokOsszege1(int n) {

int s=0;

for(int i=1; i<n; i+=1)

if(n%i==0)

s+=i;

return s;

}

private static void baratsagosSzamparok1() {

System.out.println("Barátságos számpárok 1-től 10000-ig:");

for(int i=1; i<=10000; i++)

for(int j=i+1; j<=10000; j++)

if(i==osztokOsszege1(j) && j==osztokOsszege1(i))

System.out.println("("+i+"; "+j+")");

}

2. megoldás

Kisebb módosításokkal a lépésszám csökkenthető. A baratsagosSzamparok2() eljárás külső ciklusánál figyelembe vettem, hogy a legkisebb barátságos számpár kisebb tagja nagyobb 200-nál. Mivel a barátságos számpárok tagjainak paritása mindig megegyezik (azaz mindkettő páros vagy mindkettő páratlan), így a belső ciklus j változója indítható i+2-ről és léptethető kettesével ( j+=2), és továbbra is teljesül, hogy i<j.

Az osztokOsszege2(n) függvényt is módosítottam. Mivel az 1 minden számnak osztója, illetve a 2 minden páros számnak osztója, így s lehet 3 vagy 1 és a ciklus indítható 3-ról. A páros számok esetén a számnál kisebb legnagyobb osztó maximum n/2 lehet, illetve ugyanez páratlan számok esetén n/3 lehet. Ezekre figyelve a max változó adja a ciklus léptetésének felső határát. Az i változó léptetésénél figyelembe vettem, hogy páratlan számnak csak páratlan osztói lehetnek ( i=3-mal szinkronban).

private static int osztokOsszege2(int n) {

int s=(n%2==0?3:1);

int max=(n%2==0?n/2:n/3);

int lepes=(n%2==0?1:2);

for(int i=3; i<=max; i+=lepes)

if(n%i==0)

s+=i;

return s;

}

private static void baratsagosSzamparok2() {

System.out.println("Barátságos számpárok 1-től 10000-ig:");

for(int i=200; i<=10000; i++)

for(int j=i+2; j<=10000; j+=2)

if(i==osztokOsszege2(j) && j==osztokOsszege2(i))

System.out.println("("+i+"; "+j+")");

}

3. megoldás

Az eddigi két egymásba ágyazott ciklus helyett átszervezhető a baratsagosSzamparok3() eljárás. A j>i && osztokOsszege2(j)==i feltétel kiértékelése így sokkal hatékonyabb.

private static void baratsagosSzamparok3() {

System.out.println("Barátságos számpárok 1-től 10000-ig:");

for(int i=200; i<=10000; i++) {

int j=osztokOsszege2(i);

if(j>i && osztokOsszege2(j)==i)

System.out.println("("+i+"; "+j+")");

}

Vajon milyen nagyságrendű különbségek adódnak, ha összehasonlítjuk a három megoldás futási idejét?

Az 1. megoldás futási ideje 1104156 ms, a 2. megoldásé 257055 ms, a 3. megoldásé 121 ms. A konkrét értékek helyett a nagyságrendet megfigyelve a különbség nagyon látványos.

Mindhárom megoldás helyes és megkapjuk az intervallumban található öt barátságos számpárt: (220; 284), (1184; 1210), (2620; 2924), (5020; 5564), (6232; 6368).

A bejegyzéshez tartozó teljes – időméréssel kiegészített – forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

Források:

Wikipédia – Barátságos számok
Wikipedia – Amicable numbers
www.mathe.tu-freiberg.de – Vollkommene, befreundete und gesellige Zahlen
gorbem.hu – Barátságok számok
Hasonló feladat: https://projecteuler.net/problem=21 és megoldás: http://code.jasonbhill.com/c/project-euler-problem-21/

A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 9-12. óra: Metódusok, rekurzió alkalomhoz kötődik.

Nemzetközi Pi nap

2023. január 1.2018. március 14. Szerző: Kaczur Sándor

A Pi-t ( $π$ ) mindenki ismeri. Talán sokaknak kedvenc története is van a $π$ -vel kapcsolatosan, amelyet iskolában vagy utazásai alatt szerzett. A $π$ Euklidesz geometriájában a kör kerületének és átmérőjének arányát jelöli. A $π$ irracionális szám, azaz végtelen, nem szakaszos tizedestört; másképpen számjegyei között nincs ismétlődés. A $π$ értékével a hétköznapokban 3,14-dal szokás számolni, de a tudomány területén ennél sokkal pontosabb közelítést szokás alkalmazni. A $π$ közelítése az informatikának köszönhetően akár több millió tizedesjegyig is lehetséges (például: S. Memphill: Pi to 1,000,000 places).

A nemzetközi Pi nap alkalmából (március 14) megvalósítottunk néhány – végtelen összeggel és szorzattal – $π$ közelítésre való képletet, algoritmust Java nyelven.

1. Viète-féle sor

private static void megold1() { //Viète-féle sor

double p=1, pi=1;

for(int i=11; i>1; i--) {

p=2;

for(int j=1; j<i; j++)

p=2+Math.sqrt(p);

p=Math.sqrt(p);

pi=pi*p/2;

}

pi*=Math.sqrt(2)/2;

pi=2/pi;

System.out.println(pi);

}

A módszer néhány eredménye: i=5 esetén 3.140331156954752 (2 tizedesjegyre pontos), i=10 -nél 3.1415914215112 (5 tizedesjegyre pontos), i=11 esetén 3.1415923455701176 (6 tizedesjegyre pontos).

2. Leibniz-féle sor

public static void megold2() { //Leibniz-féle sor

double s=0;

for (int i=0; i<=2500; i++)

s+=Math.pow(-1, i)/(2*i+1);

double pi=s*4;

System.out.println(pi);

}

A módszer néhány eredménye: a 24. lépéstől stabil 1 tizedesjegyre, a 626. lépéstől stabil 2. tizedesjegyre, a 2453. lépéstől stabil 3 tizedesjegyre (hiszen alternál).

3. Wallis-formula

public static void megold3() { //Wallis-formula

double p=1;

for (int i=2; i<=17000; i+=2)

p*=(1.0*i/(i-1)*(1.0*i/(i+1)));

double pi=p*2;

System.out.println(pi);

}

A módszer néhány eredménye: A 38. lépéstől 1, a 986. lépéstől 2, a 2650. lépéstől 3, a 16954. lépéstől már 4 tizedesjegyre pontos.

4. Csebisev-sor

private static void megold8() { //Csebisev-sor, V1

double s=0;

for (int k=0; k<=20; k++)

s+=(Math.pow(-1, k)*Math.pow(Math.sqrt(2)-1, 2*k+1))/(2*k+1);

double pi=s*8;

System.out.println(pi);

}

A módszer k=10 -re már 8 tizedesjegyig pontos.

A bejegyzéshez tartozó teljes forráskódot – további 8 közelítő módszer implementációjával együtt – ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 5-8. óra: Vezérlési szerkezetek alkalmához kötődik.

Péntek 13

2023. január 1.2017. október 13. Szerző: Kaczur Sándor

Sokan szerencsés vagy balszerencsés napnak tartják a péntek tizenharmadikát. Évente 1-2-3 alkalommal megtörténik, hogy a hónap 13. napja péntekre esik (minden vasárnap kezdődő hónapban). A hónap 13. napja valamivel valószínűbben péntekre esik, mint a hét bármely más napja. Átlagosan 212,35 naponként fordul elő péntek 13. Előfordulhat két egymást követő hónapban is, de akár 14 hónap is eltelhet két péntek 13 között.

A nap említése sok helyen előfordult: regényekben, filmekben, híres emberek születése vagy halála is esett péntek 13-ra. Átlag alatti közlekedési baleset szokott előfordulni ezeken a napokon – talán mert az emberek óvatosabbak. Kimutatható összefüggést/korrelációt, „péntek 13 hatást” figyeltek meg a tőzsdén is.

Hasznos lehet, ha írunk egy Java programot, amely néhány egymást követő év esetén listázza a konzolra azokat a hónapokat, amikor 13-a péntekre esik.

Tervezés

Legyen egy listFriday13(year) eljárás, amely a paraméterként átvett évben kiírja azokat a hónapokat a konzolra, amelyekben 13-a péntekre esett/esik. Például: 2017: január, október. A hónapok nevei magyar nyelven jelenjenek meg. Az adott év hónapjain végighaladó ciklus legyen hatékony. Optimalizáljunk a ciklus lépésszámára! A ciklus álljon le, ha már talált 3 hónapot (mivel nem lehet több).

1. megoldás

A megoldást a tematika Tömbök témakörében az alábbiak szerint készíthetjük el. Előismeretek: változók, operátorok, ciklusok, programozási tételek, metódusok, tömbök, String összehasonlítás. Az ismert öröknaptár algoritmusokból implementáljuk az egyiket, például:

static boolean isLeapYear(int year) {

return (year>=1582) &&

((year%4==0 && year%100!=0) || (year%400==0));

}

public static String dayOfWeek(int year, int month, int day) {

int centuryCode=2*(3-year/100%4);

int yearOfCentury=year%100;

int monthCode=new int[] {-1,

isLeapYear(year)?6:0, isLeapYear(year)?2:3, 3, 6,

1, 4, 6, 2,

5, 0, 3, 5

}[month];

int dayCode=(centuryCode+yearOfCentury+

yearOfCentury/4+monthCode+day)%7;

return new String[] {

"Sunday", "Monday", "Tuesday", "Wednesday",

"Thursday", "Friday", "Saturday"

}[dayCode];

}

public static void listFriday13v1(int year) {

String[] months={"",

"január", "február", "március", "április",

"május", "június", "július", "augusztus",

"szeptember", "október", "november", "december"};

System.out.print(year+": ");

for(int month=1, count=1; month<=12 && count<=3; month++)

if(dayOfWeek(year, month, 13).equals("Friday")) {

System.out.print(months[month]+", ");

count++;

}

System.out.println();

}

A listFriday13v1(year) eljárásban az elemi döntés egyszerű: dayOfWeek(year, month, 13).equals("Friday"). Épít az öröknaptárt megvalósító – saját – szöveget visszaadó függvényre. A függvény az algoritmus szerinti kódok előállításához ( centuryCode, monthCode, dayCode) felhasználja a szökőév ( isLeapYear(year)) függvényt, valamint két – konstansnak is tekinthető – névtelen tömböt ( new int[], new String[]).

2. megoldás

A megoldást a tematika Objektumorientált programozás témakörében az alábbiak szerint készíthetjük el. Felhasználjuk eddigi ismereteinket és a JDK beépített dátumkezelő (tároló, formázó) funkcióit (osztályok, interfészek, konstansok, felsorolások).

public static void listFriday13v2(int year) {

SimpleDateFormat dfMonth=

new SimpleDateFormat("MMMM", new Locale("hu"));

ArrayList<String> listMonths=new ArrayList<>();

for(int month=1, count=1; month<=12 && count<=3; month++) {

GregorianCalendar date=new GregorianCalendar(year, month-1, 13);

if(date.get(Calendar.DAY_OF_WEEK)==Calendar.FRIDAY) {

listMonths.add(dfMonth.format(date.getTime()));

count++;

}

System.out.println(year+": "+String.join(", ", listMonths));

}

A listFriday13v2(year) eljárás a Calendar absztrakt osztály konstansait használja fel az elemi döntéshez: date.get(Calendar.DAY_OF_WEEK)==Calendar.FRIDAY. A dátumot a GregorianCalendar konstruktora példányosítja és figyelni kell a 0-bázisú hónapkezelésre. A dátum formázása során ( dfMonth) beállítjuk a megfelelően paraméterezett ( "hu") Locale típusú objektumot és a hónap hosszú nevét kérjük ( "MMMM"). A metódus generikus listába gyűjti a kiválasztott hónapok nevét, amiket végül a String.join() függvény fűz össze a megjelenítéshez.

Eredmény

A vezérlésben egy ciklus 2017-től 2036-ig szervezve az alábbi eredményt adja:

Péntek 13 előfordulások

2017: január, október

2018: április, július

2019: szeptember, december

2020: március, november

2021: augusztus

2022: május

2023: január, október

2024: szeptember, december

2025: június

2026: február, március, november

2027: augusztus

2028: október

2029: április, július

2030: szeptember, december

2031: június

2032: február, augusztus

2033: május

2034: január, október

2035: április, július

2036: június

A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

A feladat a Java SE szoftverfejlesztő tanfolyam tematikájához kötődik a fentiek szerint: 13-16. óra: Tömbök alkalom, illetve 17-28. óra: Objektumorientált programozás alkalom.

Aki gyakorolna a témához kötődően: írjon olyan Java programot, ami listázza a konzolra a 21. század éveit olyan hónapokba csoportosítva, amikor 13-a péntekre esik. Egy év többször is előfordulhat. Például: január – 2006, 2012, 2017, 2023, 2034, 2040, 2045, 2051, 2062, 2068, 2073, 2079, 2090, 2096. A megoldásokat hallgatóinktól az ILIAS-ra, érdeklődőinktől hozzászólásban várjuk.