Címke: hatékonyság
28 blog bejegyzésnél szerepel:
 Programozási Hét 2023 – CodeWeek.eu
Programozási Hét 2023 – CodeWeek.eu
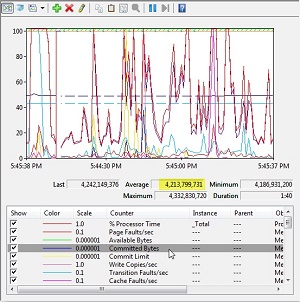 Java program memória használatának mérése
Java program memória használatának mérése
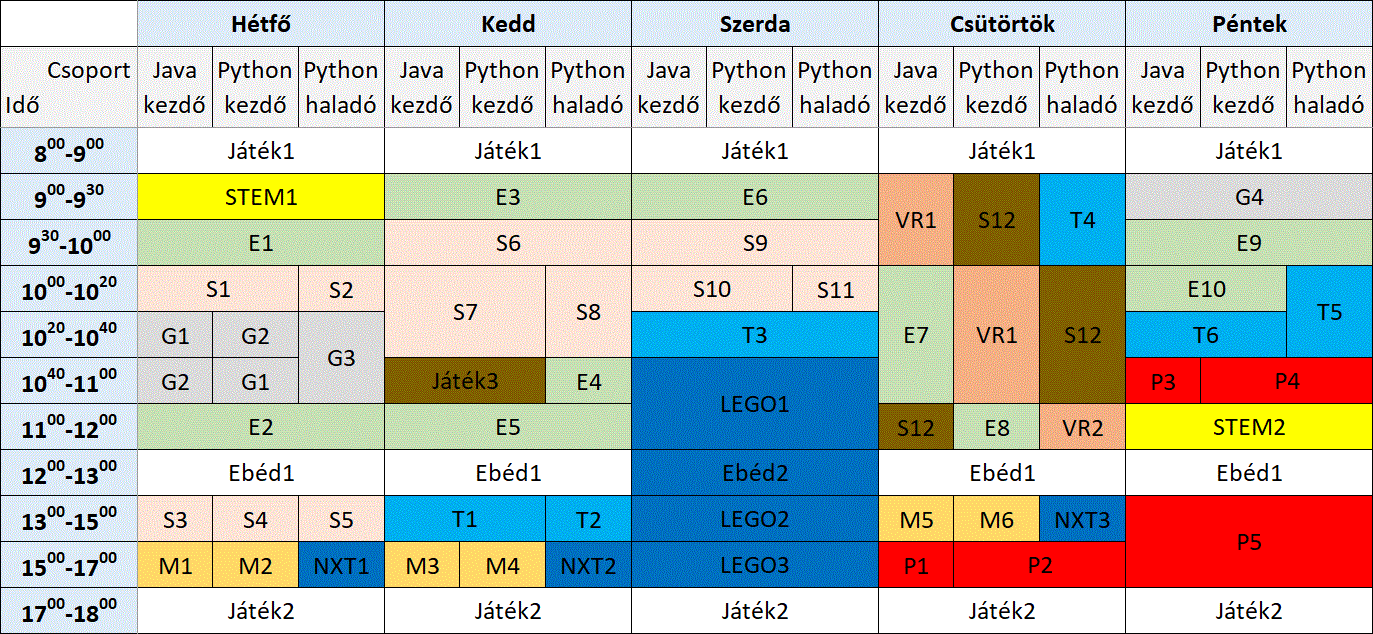
 Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
 Egy matematika érettségi feladat megoldása programozással 2023
Egy matematika érettségi feladat megoldása programozással 2023
 Programozási Hét 2022 – CodeWeek.eu
Programozási Hét 2022 – CodeWeek.eu
 Tankocka – Szókereső: rendezési algoritmusok
Tankocka – Szókereső: rendezési algoritmusok
 Programozás Java nyelven könyv - új, 2022-es kiadás
Programozás Java nyelven könyv - új, 2022-es kiadás
 Tankocka – Hozzárendeléses táblázat: Java kollekciók
Tankocka – Hozzárendeléses táblázat: Java kollekciók
 Programozási Hét 2021 – CodeWeek.eu
Programozási Hét 2021 – CodeWeek.eu
 Programozási Hét 2020 – CodeWeek.eu
Programozási Hét 2020 – CodeWeek.eu
 Doktori értekezések védése a Miskolci Egyetemen
Doktori értekezések védése a Miskolci Egyetemen
 Programozási Hét 2019 – CodeWeek.eu
Programozási Hét 2019 – CodeWeek.eu
 Programozási Hét 2018 – CodeWeek.eu
Programozási Hét 2018 – CodeWeek.eu
170 db hozzá kapcsolódó címke:
2017 (24), 2018 (24), 2019 (24), 2020 (24), 2021 (24), 2022 (24), 2023 (24), adatbázis (25), algoritmus (31), állásinterjú (10), álláskeresés (17), animáció (17), ASCII (6), atipikus megoldás (5), becslés (6), brute force (7), C# forráskód (2), ChatGPT (1), ciklusok (18), CodeWeek.eu (7), csoportmunka (10), dátumkezelés (10), Digitális Témahét (8), doktori értekezés (2), doktori képzés (4), DUE (2), Dunaújvárosi Egyetem (2), élményalapú tanulás (21), előadás műhely-napon (24), elosztott alkalmazás (14), érettségi feladat (8), értékelési szempont (6), euklideszi algoritmus (1), Euler (3), évforduló (24), fájlkezelés (29), fejtörő (11), felvételi feladat (4), fizika (7), funkcionális programozás (18), gamifikáció (33), GitHub (2), Google Charts (5), Google Cloud Platform (2), grafika (26), grafikus felhasználói felület (40), hálózatkezelés (14), hierarchikus lekérdezés (7), humor (4), IEEE Spectrum (2), Indeed (2), ingyenes esemény (34), ipar 4.0 (6), ipar 5.0 (2), játék (9), Java forráskód (63), JavaScript (6), JDBC (12), JFreeChart (7), JSON (4), JTable (7), JTree (6), kapitány (3), karrier (17), karrierváltás (14), kivételkezelés (13), kliens-szerver (7), kliensprogram (13), kollekció (32), konferencia (15), könyvajánló (4), közelítés (3), kriptoaritmetika (2), Kutatók éjszakája (8), lambda kifejezés (13), leghosszabb közös részsorozat (1), legnagyobb közös osztó (1), LEGO (3), lekérdezés (18), lépésszám (9), logikai feladat (21), logisztika (5), lottószelvény (10), MAFIOK (1), matematika érettségi feladat (8), matematika (30), ME (1), mém (7), memória használat (3), mesterséges intelligencia (12), metódus (30), Miskolci Egyetem (1), MMO (6), Multimédia az oktatásban konferencia (6), munkaerőpiac (14), munkahelyi elvárás (5), MVC (12), Naprendszer (5), naptár (26), NASA (2), Neumann János Számítógép-tudományi Társaság (8), NJSZT Multimédia az oktatásban (6), NJSZT (8), nyári tábor (2), nyilvános védés (1), OKJ szakképzés (3), okos gyár (5), objektumorientált programozás (85), OpenWeatherMap (2), optikai csalódás (2), orientáló modul (39), öröklődés (16), összefoglalás (2), osztálydiagram (7), pályaorientáció (28), pályázat (6), péntek 13 (1), Pi nap (2), Pi (2), ProgCont API (3), programozás (106), Programozási Hét (7), programozási tételek (28), projektmunka (5), publikáció (9), PYPL (2), Python (4), rajzolás (15), Reddit (2), rekurzió (9), rendezvény 2017 (5), rendezvény 2018 (10), rendezvény 2019 (11), rendezvény 2020 (12), rendezvény 2021 (6), rendezvény 2022 (8), rendezvény 2023 (10), RMI (3), robotika (12), robotprogramozás (11), soft skill (10), SQL forráskód (12), Stack Overflow (2), statisztika (11), STEM (3), Stream API (14), swing (26), szakmai előadás (31), szakmai modul (96), szimuláció (10), sztereogram (1), tananyagfejlesztés (8), tankocka (15), térinformatika (4), tervezés (41), tesztelés (21), TIOBE (2), tipikus munkanap (6), többféle megoldás összehasonlítása (37), tömb (17), tömegvonzás (5), továbbfejlesztés (23), transzformáció (8), Trendy Skills (2), UML (8), ünnepnap (13), vélemény (4), virtuális valóság (5), visszajelzés (5), XML (8)










 Az Európai Programozási Hét idén 2023. október 7-22-ig kerül megrendezésre. Ez egy önkéntesek által működtetett, alulról szerveződő kezdeményezés. Az önkéntesek saját országukban a Programozási Hét nagyköveteként népszerűsítik a programozást. Ehhez nyílt és ingyenes (online és offline) eseményeket hirdetnek meg a
Az Európai Programozási Hét idén 2023. október 7-22-ig kerül megrendezésre. Ez egy önkéntesek által működtetett, alulról szerveződő kezdeményezés. Az önkéntesek saját országukban a Programozási Hét nagyköveteként népszerűsítik a programozást. Ehhez nyílt és ingyenes (online és offline) eseményeket hirdetnek meg a 


 A
A 
 A STEM mozaikszó eléggé közismert: a tudományos-technológiai tudományágakat (természettudomány, technológia, mérnöki tudomány és matematika) foglalja egybe, interdiszciplináris megközelítésben. A STEM területén való elmélyedés során a hangsúly nem a mit tanulunk/tanítunk, hanem inkább a hogyan tanulunk/tanítunk. Nem azonnal ad kézzel fogható válaszokat, de kitartó próbálkozással – saját élménnyel – elérhető az eredmény.
A STEM mozaikszó eléggé közismert: a tudományos-technológiai tudományágakat (természettudomány, technológia, mérnöki tudomány és matematika) foglalja egybe, interdiszciplináris megközelítésben. A STEM területén való elmélyedés során a hangsúly nem a mit tanulunk/tanítunk, hanem inkább a hogyan tanulunk/tanítunk. Nem azonnal ad kézzel fogható válaszokat, de kitartó próbálkozással – saját élménnyel – elérhető az eredmény.