Kígyókocka grafikus felületen

A JavaFX grafikus felhasználói felületének és eseménykezelésének megvalósítása némileg eltér más Java GUI implementációk működésétől, például swing vagy Java3D. Főként animációk során hasznos használni. Megközelítése természetesen objektumorientált: a térbeli objektumok koordinátái, viselkedésük, transzformációkkal valósul meg, és azok is objektumok. A korábban elkészített konzolos kígyókocka programot valósítjuk meg most JavaFX GUI-val.

Ez egy két részből álló blog bejegyzés 2. része. A blog bejegyzés 1. része itt található.

A program működése

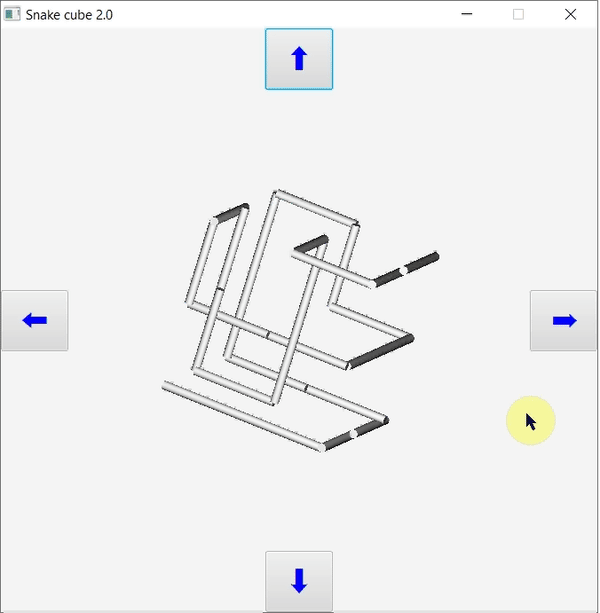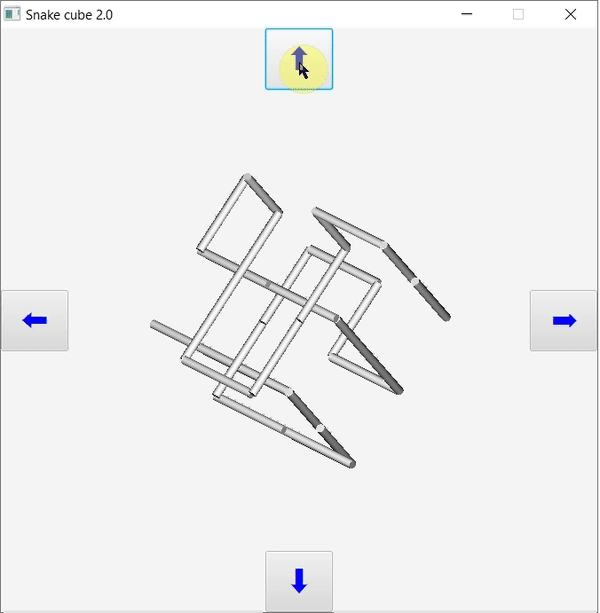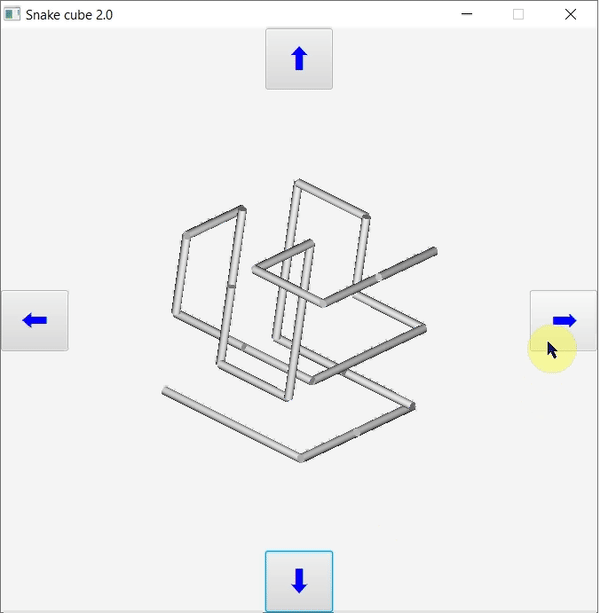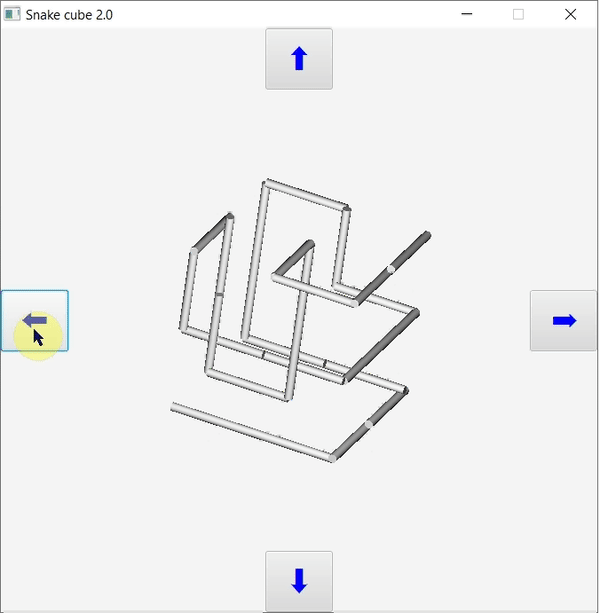
A program megvalósítása

A start() JavaFX életciklust indító eljárás felépíti a createGridUI() függvényt meghívva a felhasználói felületet (színpad/jelenet JavaFX-ben), beállítva a méreteket, címsort, és meghívja az eseménykezelésért felelős handleRotateButtons() eljárást.

@Override

public void start(Stage stage) {

StackPane root=new StackPane();

root.getChildren().add(createGridUI());

Scene scene=new Scene(root,

DRAW_AREA.getWidth()+160, DRAW_AREA.getHeight()+146);

stage.setTitle("Snake cube 2.0");

stage.setScene(scene);

stage.setResizable(false);

stage.show();

handleRotateButtons();

}

A createGridUI() függvény a grafikus felhasználói felület elemeit paraméterezi (szerepe szerint Factory metódus). Öt elemből álló rács ( GridPane osztályú grid nevű objektum) készül el, amelyre nyilakat tartalmazó nyomógombok (pl.: Button típusú btLeft objektum) kerülnek fel a négy égtájnak megfelelően, valamint rajta középen helyezkedik el a kígyókocka 3D megjelenítését megvalósító objektum. A nyilak entitásai az Unikód karaktertáblából származnak. A kígyókocka objektumot a meghívott createSnakeCube() függvény hozza létre. A Node osztályú snakeCube nevű objektum geometriai transzformációs objektumot is hozzá kell rendelni: ez most a négyirányú forgatást megvalósítani képes névtelen Rotate osztályú objektum lesz. A forgatást 5 paraméterrel célszerű beállítani (van rá megfelelő túlterhelt konstruktor), ezek rendre: szög, X, Y, Z tengely origója és a forgatás tengelye. Az objektumok tulajdonosi hierarchiája swing-es szemmel nézve szokatlannak tűnik, de szemléletben legalább azonos a Java3D és a JavaFX megvalósítás.

private GridPane createGridUI() {

String textStyle="-fx-font-size:32; -fx-text-fill: blue";

btUp.setStyle(textStyle);

btDown.setStyle(textStyle);

btLeft.setStyle(textStyle);

btRight.setStyle(textStyle);

GridPane grid=new GridPane();

grid.setHgap(10);

grid.setVgap(10);

grid.add(btUp, 1, 0);

GridPane.setHalignment(btUp, HPos.CENTER);

grid.add(btLeft, 0, 1);

grid.add(btRight, 2, 1);

grid.add(btDown, 1, 2);

GridPane.setHalignment(btDown, HPos.CENTER);

Pane drawSnakeCube=new Pane();

drawSnakeCube.setPrefSize(

DRAW_AREA.getWidth(), DRAW_AREA.getHeight());

grid.add(drawSnakeCube, 1, 1);

snakeCube=createSnakeCube();

snakeCube.getTransforms().add(

new Rotate(30, ORIGO.getX(), ORIGO.getY(), 0,

new Point3D(1, 1.5, 1.5)));

drawSnakeCube.getChildren().add(snakeCube);

return grid;

}

A createSnakeCube() függvény előállítja a színpadra/jelenetbe kikerülő kígyókockát Node osztályú objektumként. A konstans CUBE tömb egységvektor rendszerben tartalmazza a kígyót alkotó kockák középpontjait. Az első ciklus mindezt nagyítást alkalmazva skálázza. A második ciklus koordináta és pont transzformációk alkalmazásával ( moveToMidPoint: eltolás középre, rotateAroundCenter: forgatás a középpont körül) a kiinduló állapotnak megfelelő méretben és pozícióban elhelyezi a kígyó útvonalát mutató hengerobjektumokat. A konstrukciós és transzformációs műveletek esetén alkalmazkodni kell ahhoz, hogy a JavaFX koordinátarendszerben az X jobbra, az Y lefelé, a Z pedig befelé (a nézőponttól távolodva a térben) növekszik. A matematikai hátteret részletesen most nem magyarázzuk el.

private Node createSnakeCube() {

final int SCALE=100;

final Point3D Y_AXIS=new Point3D(0, 1, 0);

final int[][] CUBE=new int[][] {

{-1, 1, -1}, {0, 1, -1}, {1, 1, -1}, {1, 1, 0},

{1, 1, 1}, {0, 1, 1}, {-1, 1, 1}, {-1, 0, 1},

{-1, -1, 1}, {0, -1, 1}, {0, 0, 1}, {1, 0, 1},

{1, 0, 0}, {1, 0, -1}, {0, 0, -1}, {-1, 0, -1},

{-1, -1, -1}, {-1, -1, 0}, {-1, 0, 0}, {-1, 1, 0},

{0, 1, 0}, {0, 0, 0}, {0, -1, 0}, {0, -1, -1},

{1, -1, -1}, {1, -1, 0}, {1, -1, 1}

};

Point3D[] cube=new Point3D[CUBE.length];

for(int i=0; i<cube.length; i++)

cube[i]=new Point3D(

CUBE[i][0]*SCALE, CUBE[i][1]*SCALE, CUBE[i][2]*SCALE);

Group group=new Group();

for(int i=0; i<cube.length-1; i++) {

Point3D p1=cube[i];

Point3D p2=cube[i+1];

Point3D diff=p2.subtract(p1);

double height=diff.magnitude();

Point3D mid=p2.midpoint(p1);

Translate moveToMidpoint=new Translate(

ORIGO.getX()+mid.getX(), ORIGO.getY()+mid.getY(), mid.getZ());

Point3D axisOfRotation=diff.crossProduct(Y_AXIS);

double angle=Math.acos(diff.normalize().dotProduct(Y_AXIS));

Rotate rotateAroundCenter=

new Rotate(-Math.toDegrees(angle), axisOfRotation);

Cylinder c=new Cylinder(5, height);

c.getTransforms().addAll(moveToMidpoint, rotateAroundCenter);

group.getChildren().add(c);

}

return group;

}

A handleRotateButtons() eljárás a forgatás 4 nyíl eseménykezelésének hozzárendelést végzi el. A nyomógomb objektumok setOnAction() hozzárendelő metódusának paramétere EventHandler funkcionális interfésszel és lambda művelettel működik. A forgatás irányát hozzárendeljük a megfelelő nyomógombhoz. Ez még csak végrendelkezés a jövőre: csak definiáljuk, hogy minek kell majd történnie, ha bekövetkezik az esemény (valamelyik nyílra/nyomógombra kattint a felhasználó).

private void handleRotateButtons() {

btUp.setOnAction((event) -> { rotateSnake(Pos.TOP_CENTER); });

btDown.setOnAction((event) -> { rotateSnake(Pos.BOTTOM_CENTER); });

btLeft.setOnAction((event) -> { rotateSnake(Pos.CENTER_LEFT); });

btRight.setOnAction((event) -> { rotateSnake(Pos.CENTER_RIGHT); });

}

A rotateSnake() eljárás minden nyíl feliratú nyomógombra kattintva reagál a bekövetkezett eseményre. A rotateAxis objektum a forgatás tengelye, a paraméterként átvett direction enum-tól függ, szinkronban azzal a nyomógombbal, amelyikre kattintott a felhasználó.

Ötletek a továbbfejlesztésre

Lehetne többféle irány is, például a négy sarokba átlós vagy mélységi irányú elforgatással.
Beépülhetne többféle transzformáció is, például skálázás (kicsinyítés, nagyítás), eltolás (közelítés, távolítás).
A kígyó útvonalát mutató hengerobjektumok kirajzolásának sorrendjén lehetne változtatni, mert a megjelenítés nem tökéletes. Jelenleg néhány helyzetben lehetetlennek, Escher lehetetlen konstrukcióihoz hasonlónak tűnhet a kígyókocka. Ha a tér mélységéből a nézőpont felé közeledve rajzolnánk ki a hengerobjektumokat, akkor a 3D látvány nem sérülne.

Tanfolyamainkon JavaFX grafikus felülettel hangsúlyosan nem foglalkozunk, de egy-egy kész forráskódot közösen megbeszélünk, és össze is hasonlítjuk a swing-es változattal. Fejlesztünk játékprogramot, de inkább konzolosan, vagy swing-es ablakban, vagy webes alkalmazásként.

A grafikus felületek felépítésének megismerése fontos lépcső az objektumorientált programozás elmélyítéséhez, gyakorlásához. A grafikus felületekhez egy másik lényeges szemléletváltás is kapcsolódik, hiszen a korábbi algoritmusvezérelt megközelítést felváltja az eseményvezérelt (eseménykezelés).

Tudatosan hangsúlyozott MVC-s projektben megoldva a feladatot, a modell rétegben tárolhatnánk többféle kígyókocka megjelenítéséhez és animációjához szükséges adatszerkezetet és transzformációs objektumokat/metódusokat is és a nézet/vezérlő rétegekben biztosíthatnánk ezek közül a kijelölést/kiválasztást menüvel, ikonokkal, eszköztárral, gyorsbillentyűkkel.

A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

Tanfolyamaink orientáló moduljának 9-12. óra: Mesterséges intelligencia alkalmához kapcsolódóan a kígyókocka véletlenszerű előállítása helyett stratégiával rendelkező visszalépéses algoritmust specifikálhatunk és implementálhatunk.

Ez egy két részből álló blog bejegyzés 2. része. A blog bejegyzés 1. része itt található.

Ajánljuk a Java SE szoftverfejlesztő tanfolyam kategóriából

Java program memória használatának mérése

CHOO + CHOO = TRAIN

Egy matematika érettségi feladat megoldása programozással 2021

Munkakör, létszám, névsor lekérdezése

Naprendszer szimuláció – elméleti háttér

PDF fájl készítése