Támogatjuk a keresztrejtvények készítését Java programmal. A program grafikus felülete eszköztárból és a keresztrejtvényből áll. Az elkészült programban 10×10-től 15×15-ig beállítható négyzetrács készíthető elő. A tiltott négyzetek száma 15-től 30-ig beállítható. Mivel a tiltott négyzetek helyzete véletlenszerű, így nem biztos, hogy az elsőre jó/szerencsés lesz, ezért újragenerálható a négyzetrács. A program a tipikus követelményeknek megfelelően sorfolytonosan sorszámozza a négyzetrács elemeit, ami alapján megadhatók hozzá a vízszintes és függőleges feladványok. A program az elfogadott négyzetrácsot többféle képformátumban is el tudja menteni.
Az elkészült Java program grafikus felülete
Objektumorientált tervezés
A keresztrejtvény ábrája egy négyzetrácsból áll, amelyben rejtvénymezők helyezkednek el. A rejtvénymezőnek megfelel egy örökítéssel felüldefiniált címkekomponens. A rejtvénymezőt körülveszi egy szegély/keret, tiltott vagy sem állapotától függően fekete vagy fehér a háttérszíne, valamint van a bal felső sarkához igazított kis méretű betűvel nem kötelezően megjeleníthető sorszáma. A tiltott és sorszám tulajdonságait kell tudni beállítani és megkérdezni. Ez a feladatban a
RejtvenyMezo POJO. A négyzetrács sorai és oszlopai azonos méretűek (pixelre és darabszámra egyaránt).
Algoritmus a keresztrejtvény sorszámozására
A rejtvénymezők kétdimenziós négyzetes mátrixban/tömbben helyezkednek el. A sorszámozáshoz hasznos, ha a négyzetrácsot körbeveszi egy tiltott rejtvénymezőkből álló keret. Először a rács sorain és oszlopain végighaladó egymásba ágyazott ciklusok létrehozzák a POJO-kat úgy, hogy a négyzetrács keretén lévő rejtvénymezők tiltottak, a többi nem tiltott. Ezután véletlenszerűen ki kell választani – a még nem tiltottak közül – a szükséges mennyiségű tiltott rejtvénymezőt. Ezután sorfolytonosan sorszámozni kell azokat a rejtvénymezőket, ahol vízszintes vagy függőleges feladvány kezdődik. Ehhez is két egymásba ágyazott ciklus kell, amelyben minden még nem tiltott rejtvénymező egyre növekvő sorszámot kap, ha tőle balra tiltott és tőle jobbra nem tiltott rejtvénymező helyezkedik el, de akkor is, ha felette tiltott és alatta nem tiltott rejtvénymező található.
A keresztrejtvényt sorszámozó algoritmus Java megvalósítása
A feladványok listázhatók és kideríthető a hosszuk.
A tiltott rejtvénymezők véletlenszerű elhelyezése helyett lehetne valamilyen szabály, stratégia az egymáshoz való helyzetükre, távolságukra, közvetlen szomszédságukra vonatkozóan. Figyelembe vehetnénk valamilyen szimmetriát is, mintákat, alakzatokat is. Véletlenszerű elhelyezésük nem biztos, hogy mindig jó/szerencsés: például a tiltott rejtvénymezők körbezárhatnak egy nem tiltottat, hosszabb feladványokat nehezebb találni…
A Java SE szoftverfejlesztő tanfolyam tematikájához kötődően többféle szótárból, fájlformátumból betölthetünk a feladványokhoz használható, például 7 betűs országnevek, 2 betűs kémiai elemek, női/férfi keresztnevek, autójelek, pénznemek, szinonimák…
A Java EE szoftverfejlesztő tanfolyam tematikához kötődően többféle webes adatforrásból, Wikipédiából, szótárból, API hívásokkal letölthetünk a feladványokhoz használható listákat, meghatározásokat, kulcs-érték párokat. A swing-es felületet lecserélhetjük böngészőben futó webes GUI-ra is.
A Java adatbázis-kezelő tanfolyam tematikájához kötődően a fentiek kiegészítéseként tervezhetünk és építhetünk helyben tárolt tudástárat, adatbázist, amiből hatékonyan lekérdezve adhatunk feladványokat a keresztrejtvényhez.
Miután a fentiek szerint valahogyan – tipikusan visszalépéses algoritmussal – meghatároztuk a feladványokat, a keresztrejtvényből menthetünk kitöltött változatot is.
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
Az elmúlt 20 évben rengeteg logikai feladatokból álló tesztet állítottam össze. Kezdetben iskolai szakkörökhöz, versenyekre való felkészítéshez, tehetséggondozáshoz használtam ezeket. Ezután következett a Logikus gondolkodásra nevelő Diákműhely, amelyben ez már professzionális lett. Végül több cég/vállalkozás számára állítottam össze többféle programozói, szoftverfejlesztői tanfolyam tematikájához illeszkedően toborzáshoz, felvételihez, jelentkeztetéshez, kiválogatáshoz, szakmai interjúk során használható tesztet/feladatsort. Ezek eltérő igények szerint mérik/skálázzák a logikus gondolkodást, a problémamegoldást, az algoritmikus készségek meglétét, az összefüggések/szabályok felismerésének és alkalmazásának szintjét, a szakmai felkészültséget.
A logikus gondolkodáshoz kötődően rendszeresen szoktam előadásokat is tartani például országos rendezvényeken (Kutatók éjszakája, Digitális Témahét, Programozási Hét – CodeWeek.eu), pályaorientációs napokon és tehetséggondozó versenyek szakmai napjain tanároknak, diákoknak, főiskolás/egyetemista, Erasmus hallgatóknak.
Korábban blogoltam a népszerű Hány éves a kapitány? címmel, ahol ajánlottam 8 db magyar szakirodalmat a témában.
Most angol Mensa IQ teszt szakfolyóiratból [1, 2, 3, 4, 5] válogattam össze egy 10 feladatból álló, logikus gondolkodás mérésére alkalmas tesztet. A válaszok/megoldások név és e-mail cím megadásával automatikus válaszlevélben a bejegyzés végén hozzáférhetőek.
Logikus gondolkodás teszt – feladatok
1. feladat
Az alakzatok pozitív egész számokat jelölnek. Mi kerül a kérdőjel helyére?
2. feladat
A betűk és számok elrendezése logikus. Mi kerül a kérdőjel helyére?
3. feladat
A számok elrendezése logikus. Mi kerül a kérdőjel helyére?
4. feladat
A számok elrendezése logikus. Mi kerül a kérdőjel helyére?
5. feladat
Folytatva a sorozatot mennyi az idő a 4. analóg órán?
6. feladat
A számok elrendezése logikus. Mi kerül a kérdőjel helyére?
7. feladat
A táblázatban a piros mintával kitöltött cellák elhelyezkedése logikus. Honnan hiányzik 1 db piros mintával kitöltött cella?
8. feladat
A szimbólumok elrendezése logikus. Mi kerül a kérdőjel helyére?
9. feladat
56 db jutalomfalattal megetethető 10 háziállat, amelyek vegyesen macskák és kutyák. A macskák 5 db-ot, a kutyák 6 db-ot kapnak és végül marad 1 db jutalomfalat. Hány macska és hány kutya kap enni?
10. feladat
A 7 szám közül 6 párba állítható. Melyik szám marad ki?
A problémamegoldó, logikus gondolkodásra nevelő képzések anyagában, illetve felvételi feladatsorokban is sokszor megtalálható – többféle változatban is.
Lássunk egyet a népszerű „Hány éves a kapitány?” típusú feladatok közül!
Három elefántot kell berakodnunk – szólt a hajóskapitány az első tiszthez.
És hány évesek ezek az elefántok? – kérdezte az első tiszt.
Mindegyik elmúlt már két éves és életkoraik szorzata 2450 – volt a válasz.
Hát életkoraik összege?
Azt fölösleges elárulnom, mert abból még nem tudnád megállapítani életkorukat – mondta a kapitány, majd hozzátette: Az egyikük idősebb nálam.
Akkor már tudom, hogy hány évesek az elefántok – mondta az első tiszt.
Feltéve, hogy tényleg tudta; … hány éves a kapitány?
Hogyan használhatnánk a feladat megoldásához programozáshoz kötődő ismereteinket?
Állítsunk elő olyan három szorzótényezőt, amelyek szorzata 2450 és egyben írassuk ki az összegüket is a konzolra!
Az
i,
j,
k a három elefánt életkorát jelöli. Mivel mindegyik elmúlt két éves (és feltételezzük, hogy életkoraik egész számmal kifejezhetők), így
i=3-ról indul. Az elefántok lehetnek egyidősek, ezért
j=i-ről és
k=j-ről indul. Nincs kizárt életkor, így a változók léptethetők egyesével. Az
i,
j,
k monoton növekvő sorozatot alkot, ezért a kiírásban nem lesznek olyan sorok, amelyek csupán a szorzótényezők sorrendjében térnek el. Durva felső becslés a
100, hiszen az elefántok általában 60-70 évig élnek. Eredményül ezt kapjuk:
1
2
3
4
5
6
7
5*5*98=2450 5+5+98=108
5*7*70=2450 5+7+70=82
5*10*49=2450 5+10+49=64
5*14*35=2450 5+14+35=54
7*7*50=2450 7+7+50=64
7*10*35=2450 7+10+35=52
7*14*25=2450 7+14+25=46
Az eredményből milyen következtetés(eke)t lehet levonni és mi a megoldás?
Az egyszer előforduló összegeket ki kell zárni, mert abból az első tiszt tudná az elefántok életkorát. Többször előforduló összegként marad a 64. Tehát az elefántok lehetnek 5, 10, 49, illetve 7, 7, 50 évesek. Mivel a kapitánynál idősebb az egyik elefánt, így a kapitány nem lehet 48 éves vagy fiatalabb (mert ekkor nem lenne egyértelmű az életkora), illetve nem lehet 50 éves vagy idősebb (mert ekkor nem lenne nála idősebb elefánt). Tehát a kapitány 49 éves.
(Másképpen megközelítve: a 2450 prímtényezős felbontása 2*52*72, amiből ugyanezekre a következtetésekre juthatunk.)
A feladat további változatai
Egy hajó hosszának, az árbóc magasságának, a kapitány kisfia életkorának és a kapitány életkorának szorzata 303335. Hány éves a kapitány?
A kapitány most kétszer annyi idős, mint a hajója volt akkor, amikor a kapitány kétszer volt annyi idős, mint most a hajója. A kapitány és a hajója összesen 70 éves. Hány éves a kapitány?
A Fekete Kalóz néven elhíresült kalózkapitány egyik sikeres kalandja után kiszámíttatta saját maga és kisfia életkorának, valamint hajója hosszának a szorzatát. Az eredmény 26 159 lett, amelyet mint szerencseszámot egy medálra vésetett és mindig a nyakában hordott. Hány éves a kapitány? (A hajóhosszt méterekben mérték, és a mérőszám egész szám!)
Te vezeted az utasszállító repülőt. Budapesten felszáll 11 utas. Bécsben leszáll 5 és felszáll 9. Párizsban 1 kivételével mindenki leszáll. Hány éves a kapitány?
A kapitány hajója most 40 éves. Kétszer annyi idős, mint amennyi a kapitány volt akkor, amikor a hajó annyi idős volt, mint a kapitány most. Hány éves a kapitány?
A bejegyzéshez tartozó forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
Ajánlott irodalom
Aki kedvet kapott és beszerezne néhány könyvet – tele érdekes, gondolkodtató, kreatív, logikai feladatokkal – ajánlom az alábbiakat:
Katona, R. (szerk): Logikai egypercesek – az elme játékai, 2. kiadás, DFT-Hungária Könyvkiadó, Budapest, 2006, ISBN 963 9473 55 3
Róka, S.: 2×2 néha 5? – Paradoxonok, hibás bizonyítások, Tóth Könyvkereskedés és Kiadó Kft., Debrecen, 2008, ISBN 963 5965 24 3
Károlyi, Zs.: Csak logIQsan!, 2. javított kiadás, Typotex Elektronikus Kiadó Kft., Budapest, 2017, ISBN 963 279 693 5
G. Nagy, L.: A világ legújabb logikai rejtvényei, Magyar Könyvklub, H. n., 2001, ISBN 963 547 512 8
Haladóknak ajánlom:
Smullyan, R.: A hölgy vagy a tigris? – és egyéb logikai feladatok, 2. javított kiadás, Typotex Kiadó Kft., Budapest, 2002, ISBN 963 7546 63 4
Smullyan, R.: Mi a címe ennek a könyvnek? – Drakula rejtélye és más logikai feladványok, Typotex Elektronikus Kiadó Kft., Budapest, 1996, ISBN 963 7546 64 2
Shasha, D.: Dr. Ecco talányos kalandjai, Typotex Kiadó – SHL Hungary Kft., 2000, ISBN 963 9132 72 1
Java fejtörők – csapdák, buktató, és szélsőséges esetek. Ez egy könyv címe, amelynek szerzői J. Bloch és N. Gafter. Magyar nyelven a Kiskapu Kft. jelentette meg. A 2010-es magyar kiadás a 2005-ös angol nyelvű kiadás fordítása. A könyv weboldaláról (http://www.javapuzzlers.com), letölthető a 95 fejtörőhöz tartozó mintapéldák gyűjteménye, és elérhető a 270 oldalból minta fejezetként 28 oldalnyi tartalom 9 fejtörővel és azok részletes magyarázataival.
A két részre bontott blog bejegyzés a könyv anyagából válogatva készült el. Az első rész a bevezetés. Ez a második rész, haladó szintű példákkal. Néhány példát továbbfejlesztettem.
7. fejtörő: Mit ír ki program a konzolra?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
publicclassTest{
staticvoidworkHard(){
try{
workHard();
}
finally{
workHard();
}
}
publicstaticvoidmain(String[]args){
workHard();
System.out.println("Hello World!");
}
}
Kivételkezelés nélkül arra számítanánk, hogy a
Hello World! nem jelenik meg a konzolon, mert a
wordHard() metódus feltétel nélkül rekurzív módon folyamatosan újrahívja önmagát és az emiatt keletkező
StackOverflowError hibával elszáll a program. A kivételkezelés természetesen módosítja a program működését.
Ha azt feltételezzük, hogy minden
Throwable utódosztályból futás közben létrehozott objektum kivételkezeléssel elkapható, akkor végtelen ciklusnak tűnik a vezérlés, hiszen a
try blokkban hibát okozó metódushívásra a
finally blokkban újra ugyanannak a metódusnak a meghívásával reagálunk, amelyik korábban a hibát kiváltotta. Ez a gondolatmenet tévút. A kulcsszó a rekurzív vezérlést megvalósító verem adatszerkezet mérete. Részletes indoklás a blog bejegyzés végén található.
8. fejtörő: Mit ír ki program a konzolra?
1
2
3
4
5
6
7
8
9
publicclassNull{
staticvoidgreet(){
System.out.println("Hello World!");
}
publicstaticvoidmain(String[]args){
((Null)null).greet();
}
}
Természetesen
NullPointerException-re gyanakszunk, pedig a program hibátlanul működik. A kulcsszó a statikus metódusok minősítése, vagyis annak jelölése, hogy melyik osztálytól vagy objektumtól kérjük annak végrehajtását. Részletes indoklás a blog bejegyzés végén található.
Arra számítunk, hogy a kiírás
1999-12, de ehelyett
20001-et látunk a konzolon. Tudjuk, hogy a
Date osztály jó része már deprecated és ezen próbáltak javítani a
Calendar osztállyal. Bár ne tették volna. A kulcsszó az ős dátumkezelést megvalósító API rejtelmeiben van. Részletes indoklás a blog bejegyzés végén található.
10. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
classX{
staticclassY{
staticStringZ="Black";
}
staticCY=newC();
}
classC{
StringZ="White";
}
publicclassTest{
publicstaticvoidmain(String[]args){
System.out.println(X.Y.Z);
}
}
Nem tűnik egyértelműen eldönthetőnek a helyzet, ezért szintaktikai hibára gyanakodhatunk. Azonban a forráskód helyes, a program futás közben sem dob kivételt/hibát és a konzolon megjelenik a
White. Szokatlan, hogy nagybetűvel konstansokat szokás jelölni, pedig nincs erre utaló
final a forráskódban. A kulcsszó a sorrendiségen van, ha ugyanabban a hatókörben/blokkban van azonos nevű változó és típus/osztály. Részletes indoklás a blog bejegyzés végén található.
11. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
importjava.util.Random;
publicclassTest{
privatestaticRandomr=newRandom();
privatestaticvoidswap(Object[]a,inti,intj){
Objecttemp=a[i];
a[i]=a[j];
a[j]=temp;
}
publicstaticObject[]shuffle(Object[]a){
for(inti=0;i<a.length;i++)
swap(a,i,r.nextInt(a.length));
returna;
}
publicstaticvoidmain(String[]args){
String[]s1={"alma","körte","barack","dinnye"};
for(Objecto:shuffle(s1))
System.out.print(o+", ");
System.out.println();
}
}
A program helyes és egyértelműnek tűnik. A konzolra az
s1 szövegtömb elemei kerülnek ki véletlenszerűen összekeverve. Finomítsunk a kérdésen. Vajon minden lehetséges permutáció azonos eséllyel fordul elő? Ha ez a kérdés egyáltalán felmerül, akkor a válasz nyilván nem. A kulcsszó most egy kis matematika. Részletes indoklás a blog bejegyzés végén található.
12. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
8
9
10
importjava.util.Arrays;
publicclassTest{
publicstaticvoidmain(String[]args){
Integer[]array={3,1,4,1,5,9};
Arrays.sort(array,
(Integeri1,Integeri2)->i1<i2?-1:(i2>i1?1:0));
System.out.println(Arrays.toString(array));
}
}
Ez a forráskód nem úgy működik, ahogyan a könyv írja. Meglepő módon nem a
[3,1,4,1,5,9]-et adja, hanem az
[1,1,3,4,5,9]-et. Némi indoklás a blog bejegyzés végén található.
Részletes indoklások
7. fejtörő: ha a
try blokkban folyamatosan meghívja saját magát a
workHard() metódus, akkor előbb-utóbb betelik a verem. Ekkor a
finally blokkra kerül a vezérlés, ahonnan újra hívja saját magát a
workHard() metódus. Persze követni kell, hogy a rekurzió végrehajtása során a lefelé haladó vagy a felszálló ágon vagyunk és nem mindegy, hogy melyik szinten. A háttérben egy teljes bináris fa bontakozik ki, amelynek mélysége azonos a verem méretével, mélységi korlátjával. Ezt a teljes bináris fát járja be a program, azaz mélységi fabejárás. Egy n mélységű teljes bináris fa elemeinek száma 2n-1. A verem mérete a virtuális gép beállításaitól függ, több ezer mélységű is lehet. Végtelen ciklusról tehát nincs szó. Ugye milyen izgalmas? További részletek a könyv 100-102. oldalán találhatók.
8. fejtörő: a végrehajtás kiértékeli a statikus
greet() metódus hívásának minősítő kifejezését, de figyelmen kívül hagyja a kapott értéket. A metódust végrehajthatnánk
Null.greet()-ként vagy közvetlenül (minősítés nélkül) meghívva is. További részletek a könyv 122-124. oldalán találhatók.
9. fejtörő: a
Date osztály a hónapokat nulla bázissal kezeli, ezért csak 0-11-ig “van értelme”. Számíthatnánk a tömb vagy szöveg túlindexelésénél tapasztaltakhoz hasonlóan kivételre, de nem ez történik. A 12. hónap a következő év első/nulladik hónapját jelöli. Ezért látjuk a konzolon a
2000-et, amit egy kötőjel követ. A
Date.getDay() deprecated metódus pedig a dátumobjektumban tárolt nap adott héten (nem hónapban!) elfoglalt helyét adja meg, ami nullával, azaz vasárnappal indul. Tehát a konzolon megjelenő
1 nem a 2000. januárt jelenti, hanem azt, hogy a 2000. január 31. hétfőre esik. Aki ezek után meri használni a régi dátumkezelő API-t, magára vessen. További részletek a könyv 141-143. oldalán találhatók.
10. fejtörő: ha ugyanabban a hatókörben/blokkban van azonos nevű változó és típus/osztály, akkor a változó neve az elsődleges. Ha betartjuk a névadási konvenciókat (
ClassName,
objectName,
CONSTANT_NAME), akkor nem adódhatnak ilyen gondok. Még egy csavar van: ha az előző elnevezési módosításokat megtesszük, akkor a program a
Black-et írja ki a konzolra. További részletek a könyv 161-163. oldalán találhatók.
11. fejtörő: konkrét esetből általánosítunk. 4 elemre a ciklus 4-szer hajtódik végre és minden lépésben kiválaszt egyet a 0 és az 3 indexű elemek közül, ami 44=256-féle lehetséges eredményt ad. Ha az
r objektum jól működik, akkor az egyes futások esélye/valószínűsége megegyezik. 4 elemű tömb elemeinek 4!=24 (faktoriális) féle permutációja (lehetséges sorrendje) van. Mivel a 256 nem osztható 24-gyel, így biztos, hogy a
shuffle() metódus bizonyos permutációkat gyakrabban állít elő, mint másokat. Általánosan: nn nem osztható n!-sal, ha n>2 egész szám. Vajon mi történik, ha egy 52 lapos pakli kártyát keverünk össze? Vajon milyen érdekességet vet ez fel? Minden poént nem lövünk le itt a blogban. További részletek a könyv 228-232. oldalán találhatók.
12. fejtörő: ez a tankönyv utolsó példája. A felvetett gondolat nagyon frappáns: az összehasonlító rész „ha fej, én nyerek, ha írás, te veszítesz” tüneteitől szenved. További részletek a könyv 232-233. oldalán találhatók.
Állásinterjúkon időnként visszaköszönnek hasonló fejtörők, de ezekkel óvatosan kell bánni. Egy programozási nyelv „joghézagainak”, buktatóinak, szélsőséges eseteinek ismerete a könyv szintjét elérő ismeretanyaggal nem lehet elvárt még egy meghirdetett senior pozíció esetén sem. Ezen fejtörők ismerete (vagy nem tudása) egy jelöltről nem árulja el a mindennapokban használható szakmai tudás meglétét/hiányát. De nyilván aki szakmailag folyamatosan fejlődik és mindenféle keretrendszert alkotó forráskódokban turkál, elemez, előbb-utóbb találkozik ezekkel/ilyenekkel.
Tanfolyamainkon nem kifejezetten foglalkozunk hasonló problémákkal, de azért időnként feszegetjük a határokat. Természetesen részletesen indokoljuk, ha előkerül valamilyen hasonló eset. Általánosságban nem célunk, hogy extrém eseteken keresztül, a programozási nyelv gyenge pontjaira kihegyezve oktassuk a Java programozási nyelvet.
Java fejtörők – csapdák, buktató, és szélsőséges esetek. Ez egy könyv címe, amelynek szerzői J. Bloch és N. Gafter. Magyar nyelven a Kiskapu Kft. jelentette meg. A 2010-es magyar kiadás a 2005-ös angol nyelvű kiadás fordítása. A könyv weboldaláról (http://www.javapuzzlers.com), letölthető a 95 fejtörőhöz tartozó mintapéldák gyűjteménye, és elérhető a 270 oldalból minta fejezetként 28 oldalnyi tartalom 9 fejtörővel és azok részletes magyarázataival.
Messze nem mai az anyag, de teljesen örökzöld. Ma is kifejezetten igazán izgalmas átgondolni ezeket a fejtörőket. Biztos vagyok benne, hogy az igazán profiknak is nyújt újdonságot egy-egy fejtörő mögötti részletes magyarázat. Sokszor kiderül az a ravasz és csavaros magyarázatok között, hogy mire gondolt a költő, azaz mi volt/lehetett a Java programozási nyelv tervezése során a szakemberek elképzelése, illetve előfordultak-e kompromisszumok, amiknek persze következményei vannak.
Két – literálként megadott – egész szám összegét kell kapni. Két egyforma értéket várunk:
66666. Mégsem ezt kapjuk. Az első kiírás
66666-ot, a második
17777-et jelenít meg a konzolon. A kulcsszó a különböző egész literálok megadása. Részletes indoklás a blog bejegyzés végén található.
2. fejtörő: Mit ír ki program a konzolra?
1
2
3
4
5
6
7
8
9
10
publicclassTest{
publicstaticvoidmain(String[]args){
Stringpig="length: 10";
Stringdog="length: "+pig.length();
System.out.println("Animals are equal: "+pig==dog);
System.out.println(("Animals are equal: "+pig)==dog);
System.out.println("Animals are equal: "+(pig==dog));
System.out.println("Animals are equal: "+pig.equals(dog));
}
}
Szöveges literálokat hasonlítunk össze, amelyek egyforma (
length:10) tartalommal jönnek létre. Döntések eredményeit várjuk,
boolean típusú változókat. Négy sorba tördelve ezt kapjuk:
false,
false,
Animals are equal:false,
Animals are equal:true. A kulcsszó a művelet végrehajtás sorrendje, másképpen kifejezések kiértékelési sorrendje. Részletes indoklás a blog bejegyzés végén található.
3. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
8
9
10
11
/*
* Generated by the IBM IDL-to-Java compiler, version 1.0
* from F:\TextRoot\apps\a1\units\include\PolicyHome.idl
* Wednesday, June 17, 1998 6:44:40 o'clock AM GMT+00:00
*/
publicclassTest{
publicstaticvoidmain(String[]args){
System.out.print("Hell");
System.out.println("o World!");
}
}
Természetesen a megjegyzéssel nem törődünk és arra gondolunk, hogy a konzolon a
Hello World! jelenik meg (a két kiíró utasítás eredménye egyetlen sorban egymás után) és nem is értjük, hogy mi a kérdés. Nyilván a helyzet nem ilyen triviális. A program nem futtatható. A kulcsszó az unikód escape szekvencia (védőkarakter). Részletes indoklás a blog bejegyzés végén található.
4. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
publicclassTest{
publicstaticvoidmain(String[]args){
System.out.print("browser:");
https://www.google.com;
System.out.println(":maximize");
}
}
Nyilván szintaktikai hibát feltételezünk, de a program hibátlan és futtatva ezt látjuk a konzolon:
browser::maximize. A kulcsszó a címke/utasításcímke. Részletes indoklás a blog bejegyzés végén található.
5. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
publicclassTest{
privatestaticbooleandecision(){
try{
returntrue;
}
finally{
returnfalse;
}
}
publicstaticvoidmain(String[]args){
System.out.println(decision());
}
}
Gyanús a helyzet. Adott egy függvény, aminek kötelezően van visszatérési értéke. Ez rendben van. Tudjuk, hogy a
return utasítás kiugrik a függvényből, eljárásból, ciklusból. A kivételkezeléshez kötődő nyelvi kulcsszavakat is ismerjük:
try,
catch,
finally,
throw,
throws. Ezek működését is ismerjük. Azt feltételezhetjük, hogy a
try blokkból kiugrunk
true értékkel és a
decision() függvényt meghívó
main() metódusba visszatérve kiíródik a konzolra, hogy
true. Mintha a
finally blokk nem is lenne. Nem így történik. A programot futtatva
false jelenik meg a konzolon. A kulcsgondolat a
finally blokk végrehajtásának vezérléséhez kapcsolódik. Részletes indoklás a blog bejegyzés végén található.
6. fejtörő: Mit ír ki a program a konzolra?
1
2
3
4
5
6
7
publicclassTest{
publicstaticvoidmain(String[]args){
Stringhello="Hello World!";
for(inti=0;i<hello.length();i++)
System.out.write(hello.charAt(i));
}
}
Már biztosan gyanakszunk, de azért a
Hello World!-öt várjuk a konzolon. Ehelyett nem jelenik meg semmi. A kulcsszó a puffer ürítés. Részletes indoklás a blog bejegyzés végén található.
Részletes indoklások
1. fejtörő:
int típusú literál az
54321, de
long típusú literál az
5432l. Az
1 – mint numerikus karakter – nem egyezik meg a kis
l betűvel. Tanulság: használjuk nagy
L betűt a
long típusú literálok végén. További részletek a könyv 11-12. oldalán találhatók.
2. fejtörő: a konkatenálást végző
+ operátor erősebben kötődik, mint a két objektumreferencia azonosságát eldöntő
== operátor. Az első kiírásban látható művelet igazából a második kiírásban látható zárójeles formában kerül végrehajtásra. A harmadik kiírást az magyarázza, hogy a
String típusú literálokat memóriacímeik és nem a bennük tárolt karaktersorozat/érték alapján hasonítódnak össze. A helyes gondolatmenet implementálását a negyedik kiírás tartalmazza: (megegyezik-e a két szövegliterál tartalma). További részletek a könyv 29-31. oldalán találhatók.
3. fejtörő: a megjegyzés 3. sorában található
\u karaktert 4 db hexadecimális számnak kellene követnie. Ez hiányzik, ami szintaktikai hibát jelent. További részletek a könyv 33-34. oldalán találhatók.
4. fejtörő: az URL-ben lévő : egy ugyanolyan címke, amit a
switch utasításban a
case ágaknál szokás használni. Ez így is megengedett, de teljesen haszontalan. További részletek a könyv 47-48. oldalán találhatók.
5. fejtörő: a kivételkezelési mechanizmus úgy működik, hogy a
try blokkban lévő utasításoktól függetlenül – akár volt kivétel akár nem, akár
return utasítást tartalmaz a
try blokk – a
finally blokk mindenképpen végrehajtódik. Ebben az esetben a kivételkezelési mechanizmus erősebb. További részletek a könyv 77-78. oldalán találhatók.
6. fejtörő: a
System.out egy
PrintStream osztályú objektum. Többnyire automatikusan ürítik az átmeneti tárolóját az ezt használó utasítások, például
System.out.print() és
println(). A
write() metódus nem üríti ezt a puffert. További részletek a könyv 195-196. oldalán találhatók.
Tanfolyamainkon nem kifejezetten foglalkozunk hasonló problémákkal, de azért időnként feszegetjük a határokat. Természetesen részletesen indokoljuk, ha előkerül valamilyen hasonló eset. Általánosságban nem célunk, hogy extrém eseteken keresztül, a programozási nyelv gyenge pontjaira kihegyezve oktassuk a Java programozási nyelvet.
Weboldalunkon cookie-kat (sütiket) használunk, melyek célja, hogy teljesebb szolgáltatást nyújtsunk látogatóink részére. További böngészésével hozzájárul ezek használatához. ElfogadAdatkezelési szabályzat
Privacy Overview
This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.
Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.
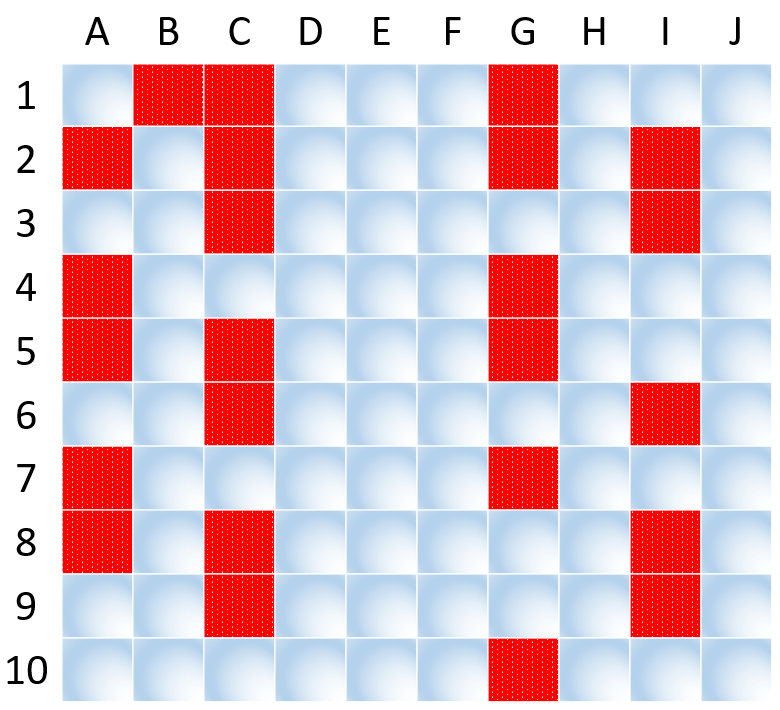
Támogatjuk a keresztrejtvények készítését Java programmal. A program grafikus felülete eszköztárból és a keresztrejtvényből áll. Az elkészült programban 10×10-től 15×15-ig beállítható négyzetrács készíthető elő. A tiltott négyzetek száma 15-től 30-ig beállítható. Mivel a tiltott négyzetek helyzete véletlenszerű, így nem biztos, hogy az elsőre jó/szerencsés lesz, ezért újragenerálható a négyzetrács. A program a tipikus követelményeknek megfelelően sorfolytonosan sorszámozza a négyzetrács elemeit, ami alapján megadhatók hozzá a vízszintes és függőleges feladványok. A program az elfogadott négyzetrácsot többféle képformátumban is el tudja menteni.
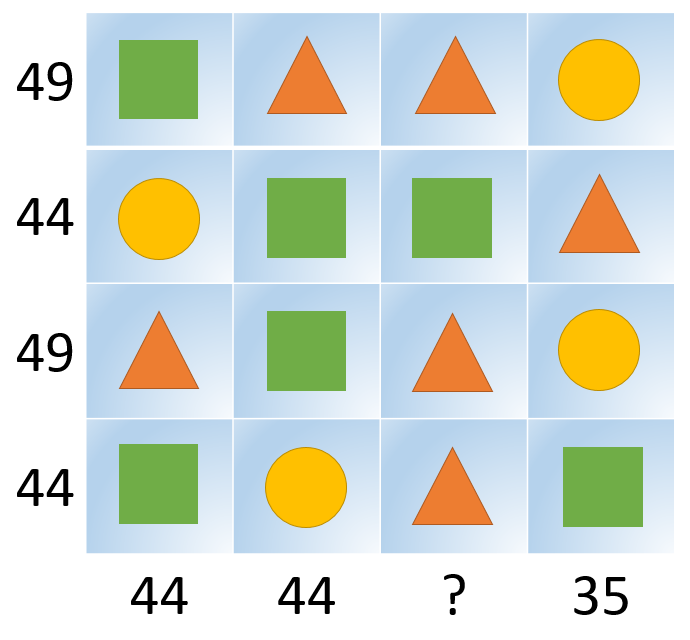
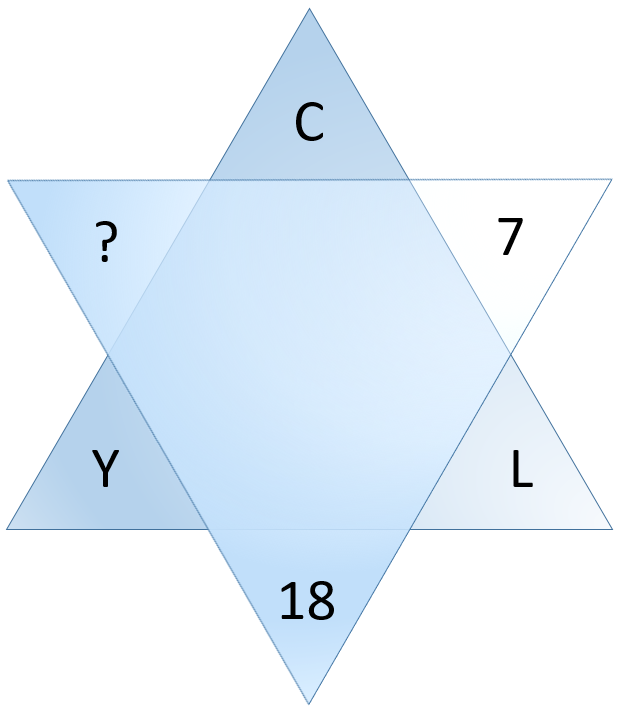
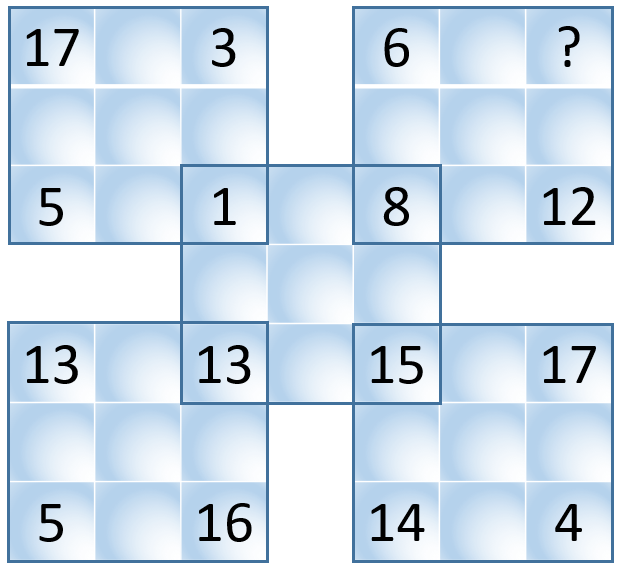
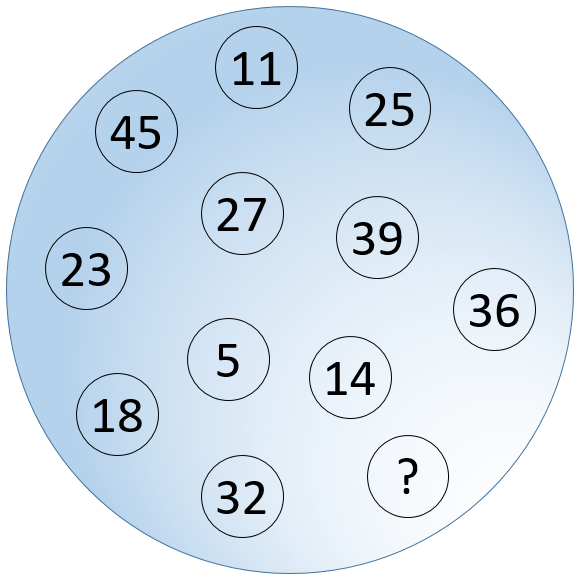
Az elmúlt 20 évben rengeteg logikai feladatokból álló tesztet állítottam össze. Kezdetben iskolai szakkörökhöz, versenyekre való felkészítéshez, tehetséggondozáshoz használtam ezeket. Ezután következett a Logikus gondolkodásra nevelő Diákműhely, amelyben ez már professzionális lett. Végül több cég/vállalkozás számára állítottam össze többféle programozói, szoftverfejlesztői tanfolyam tematikájához illeszkedően toborzáshoz, felvételihez, jelentkeztetéshez, kiválogatáshoz, szakmai interjúk során használható tesztet/feladatsort. Ezek eltérő igények szerint mérik/skálázzák a logikus gondolkodást, a problémamegoldást, az algoritmikus készségek meglétét, az összefüggések/szabályok felismerésének és alkalmazásának szintjét, a szakmai felkészültséget.
Java fejtörők – csapdák, buktató, és szélsőséges esetek. Ez egy könyv címe, amelynek szerzői J. Bloch és N. Gafter. Magyar nyelven a Kiskapu Kft. jelentette meg. A 2010-es magyar kiadás a 2005-ös angol nyelvű kiadás fordítása. A könyv weboldaláról (