Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Lássuk, hogyan valósítható meg Java programozási nyelven a kép élesítése!
A kép adatszerkezete
Adott egy képfájl. Formátuma a tipikus, feldolgozhatók (JPG, GIF, PNG, WebP) egyike. Ezek rasztergrafikus képformátumok. Lekérdezhető a dimenziója: ez képpontban (pixelben) jelenti a kép szélességét (width) és a kép magasságát (height). A vászontechnika meghatározza a kép origóját (0, 0) és a képpontok kétdimenziós koordinátapárját. A kép origója a bal felső sarokban van. A kép oszlopai (column) jobbra haladva növekvő módon, a kép sorai (row) lefelé haladva növekvő módon számozottak. Egy pixel koordinátapárja (c, r) alakban írható le. Minden pixel három szín kombinációjaként áll elő (r, g, b). Másképpen: a piros, zöld és kék összetevők aránya alapján meghatározott. A tipikus színmélység alapján a színek külön-külön 256-félék lehetnek, és ezeket 0-tól 255-ig egész szám képviseli. A 0 az adott szín hiányát, a 255 a szín teljes intenzitását jelenti.
A kép élesítéséhez használható szűrőmátrixok
A kép élesítése során szűrőt alkalmazunk a kép belső pixeleire. A kép 4 szélén lévő pixeleket nem változtatjuk. Többféle szűrő közül választhatunk, íme két példa:
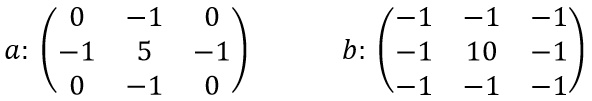
A három színösszetevőre külön-külön kell alkalmazni a szűrőt. Az aktuális pixel – amire alkalmazzuk a szűrőt – a 3×3-as mátrix középső eleméhez igazítva szorzóértékeket tartalmaz. A konkrét eset: az a mátrix esetén az 5 érték a 2. sor 2. oszlopában helyezkedik el; ennek a közvetlen szomszédos pixeleire a -1 értékek, átlós szomszédaira pedig a 0 értékek vonatkoznak. Eredményül a szűrt pixel színeit kapjuk meg külön-külön. Ha a kapott értékek kisebbek 0-nál, akkor nullázzuk őket. Ha a kapott értékek nagyobbak 255-nél, akkor beállítjuk azokat 255-re. Az a szűrőmátrix kevésbé élesít, a b szűrőmátrix erősebben élesít.
Természetesen sok más képélességhez köthető szűrő is van még. Olyanok is vannak, ahol nem csak a közvetlen szomszédos pixeleket veszi figyelembe az algoritmus. További kulcsszavak a témához kötődően: digitális képfeldolgozás, lokális operátor, korreláció, konvolúció, átlagszűrő, mediánszűrő, zajszűrő, Laplace-szűrő.
A kép élesítését megvalósító Java forráskód-részlet
A fenti a mátrixot a
SHARP_FILTER konstans kétdimenziós tömb tárolja. A paraméterként átvett
BufferedImage típusú
img1 objektum kép pixeleinek végigjárását ütközőként segíti a
w szélesség és
h magasság. A
data egydimenziós tömb sorfolytonosan tárolja a kép pixeleit. Az
if elágazó utasítás igaz ága kezeli a kép 4 szélét (változatlanul hagyott másolt színek). Az
if hamis ága a belső pixelekre alkalmazza a szűrőmátrixot. A
red,
green,
blue változók tartalmazzák az aktuális pixel színeit, amelyekbe az eredeti pixelre alkalmazott szűrő által szorzott értékek kerülnek, „belekényszerítve” a 0-255 zárt intervallumba. Végül az eredményül visszaadott
img2 kép pixelei kerülnek beállításra. Az alábbi
sharpenEffect() függvény mindezt megoldja az alábbiak szerint:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
public static BufferedImage sharpenEffect(BufferedImage img1) { final int[][] SHARP_FILTER={ { 0, -1, 0}, {-1, 5, -1}, { 0, -1, 0} }; Color[][] colorArray=new Color[3][3]; int w=img1.getWidth(), h=img1.getHeight(), i=0; int[] data=new int[w*h]; for(int y=0; y<h; y++) for(int x=0; x<w; x++) { if(y==0 || x==0 || y==h-1 || x==w-1) data[i]=img1.getRGB(x, y); else { for(int c=y-1; c<=y+1; c++) for(int r=x-1; r<=x+1; r++) colorArray[x-r+1][y-c+1]=new Color(img1.getRGB(r, c)); int red=0, green=0, blue=0; for(int c=0; c<=2; c++) for(int r=0; r<=2; r++) { red+=SHARP_FILTER[r][c]*colorArray[r][c].getRed(); green+=SHARP_FILTER[r][c]*colorArray[r][c].getGreen(); blue+=SHARP_FILTER[r][c]*colorArray[r][c].getBlue(); } red=(red<0)?0:(red>255?255:red); green=(green<0)?0:(green>255?255:green); blue=(blue<0)?0:(blue>255?255:blue); Color c2=new Color(red, green, blue); data[i]=c2.getRGB(); } i++; } BufferedImage img2= new BufferedImage(w, h, BufferedImage.TYPE_INT_RGB); img2.setRGB(0, 0, w, h, data, 0, w); return img2; } |
A metódus meghívása a fájlkezelést is tartalmazó vezérlőmetódusban például így történhet:
|
|
public static void main(String[] args) { try { BufferedImage imageSource=ImageIO.read( new File("./images/Traditional-Japanese-Garden.jpg")); BufferedImage imageSharpen=sharpenEffect(imageSource); ImageIO.write(imageSharpen, "jpg", new File("./images/Traditional-Japanese-Garden-sharpen.jpg")); } catch(Exception e) { // } } |
Az eredeti és élesített képek összehasonlítása
A bal oldalon az eredeti kép, a jobb oldalon az a mátrixszal élesített kép látható:

A bal oldalon az eredeti kép, a jobb oldalon a b mátrixszal élesített kép látható:

A látvány alapján fontos kiemelni, hogy másképpen is lehet összehasonlítást végezni. Például: színtérkép, színmélység, színösszetevők aránya (hisztogram).
Ötletek továbbfejlesztésre
- Konzolos program átvehetné parancssori paraméterként a szűrőmátrixot, vagy annak nevét, kódját, egyes értékeit.
- Grafikus felületű programban vízszinten
JScrollBar GUI komponens(ek) segítségével paraméterezhető, kigörgethető lehetne a szűrőmátrix szélsőértéke(i).
- A fenti effektek a kép összes pixelét érintik. GUI felületen megoldható az is, hogy ki tudjuk jelölni a kép egy-egy részét, amire alkalmazni szeretnénk az effektek. Ez a kijelölés többféle lehet, például téglalap alakú, szabálytalan, átlátszó, adott vagy adotthoz hasonló árnyalatú színű, vagy valaminek a körvonala.
- Egy mappában lévő összes képre alkalmazható effekt, előnézettel, képfájlonként megerősítéssel, jóváhagyással, csoportos kijelöléssel, szűrővel.
- Szürkeskála effekt megvalósítása és tesztelése az alábbi forráskód-részlettel:
|
|
Color c1=new Color(img1.getRGB(x, y)); int gray=(int) (0.21*c1.getRed()+0.72*c1.getGreen()+0.07*c1.getBlue()); Color c2=new Color(gray, gray, gray); |
- Homályosítás effekt megvalósítás és tesztelése a 4 élszomszéd színeinek átlagolásával, így:
|
|
Color cTop=new Color(img1.getRGB(x, y-1)), cRight=new Color(img1.getRGB(x+1, y)), cBottom=new Color(img1.getRGB(x, y+1)), cLeft=new Color(img1.getRGB(x-1, y)); int r=(cTop.getRed()+cRight.getRed()+ cBottom.getRed()+cLeft.getRed())/4, g=(cTop.getGreen()+cRight.getGreen()+ cBottom.getGreen()+cLeft.getGreen())/4, b=(cTop.getBlue()+cRight.getBlue()+ cBottom.getBlue()+cLeft.getBlue())/4; Color c2=new Color(r, g, b); |
A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.
A Java SE szoftverfejlesztő tanfolyamunkon, a szakmai modul Objektumorientált programozás témakörét követő 29-36. óra Grafikus felhasználói felület alkalmain már tudunk egyszerűbb GUI programot tervezni, kódolni, tesztelni, kiegészítve a 37-44. óra Fájlkezelés alkalmaihoz kötődő példaprogramokkal.
 Kép élesítése effektus működése
Kép élesítése effektus működése Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023 Tankocka – Rövid válasz: Java konstansok
Tankocka – Rövid válasz: Java konstansok Egy matematika érettségi feladat megoldása programozással 2022
Egy matematika érettségi feladat megoldása programozással 2022 Egy matematika érettségi feladat megoldása programozással 2018
Egy matematika érettségi feladat megoldása programozással 2018 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017









 A
A 
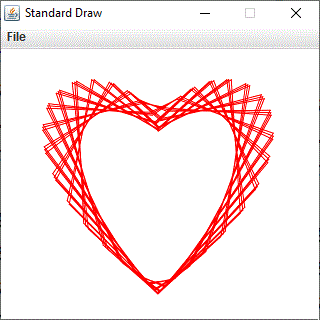
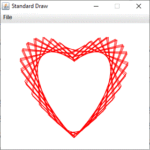 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.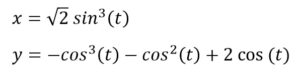

 Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).
Ismert számos képfeldolgozó, képjavító effektus. Az egyszerűbb effektusok elérhetők ingyenes web- és mobil alkalmazásokban, PowerPointban. Az összetettebb (művészi) effektusokhoz, szűrőkhöz már érdemes professzionális eszközt használni, ilyen például az Adobe Photoshop. Ezek a belépő szint képeffektusai kulcsszavakban: élesítés (sharpen), homályosítás (blur), elmosódás (gaussian blur), folyadékszerű rajz (liquid), olajfestmény (oil painting), öregítés (sepia), szürkeskála (grayscale).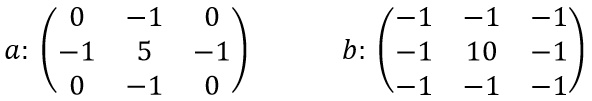


 Adott egy mappában lévő sok-sok képfájl, többféle formátumban, kiterjesztéssel. A feladat az, hogy időzítve jelenítsük meg ezeket a képeket véletlen sorrendben saját fejlesztésű Java program segítségével. A tervezés során áttekintünk többféle lehetőséget. Bemutatjuk a megoldáshoz szükséges lépéseket és a program működését.
Adott egy mappában lévő sok-sok képfájl, többféle formátumban, kiterjesztéssel. A feladat az, hogy időzítve jelenítsük meg ezeket a képeket véletlen sorrendben saját fejlesztésű Java program segítségével. A tervezés során áttekintünk többféle lehetőséget. Bemutatjuk a megoldáshoz szükséges lépéseket és a program működését.

 A STEM mozaikszó eléggé közismert: a tudományos-technológiai tudományágakat (természettudomány, technológia, mérnöki tudomány és matematika) foglalja egybe, interdiszciplináris megközelítésben. A STEM területén való elmélyedés során a hangsúly nem a mit tanulunk/tanítunk, hanem inkább a hogyan tanulunk/tanítunk. Nem azonnal ad kézzel fogható válaszokat, de kitartó próbálkozással – saját élménnyel – elérhető az eredmény.
A STEM mozaikszó eléggé közismert: a tudományos-technológiai tudományágakat (természettudomány, technológia, mérnöki tudomány és matematika) foglalja egybe, interdiszciplináris megközelítésben. A STEM területén való elmélyedés során a hangsúly nem a mit tanulunk/tanítunk, hanem inkább a hogyan tanulunk/tanítunk. Nem azonnal ad kézzel fogható válaszokat, de kitartó próbálkozással – saját élménnyel – elérhető az eredmény.