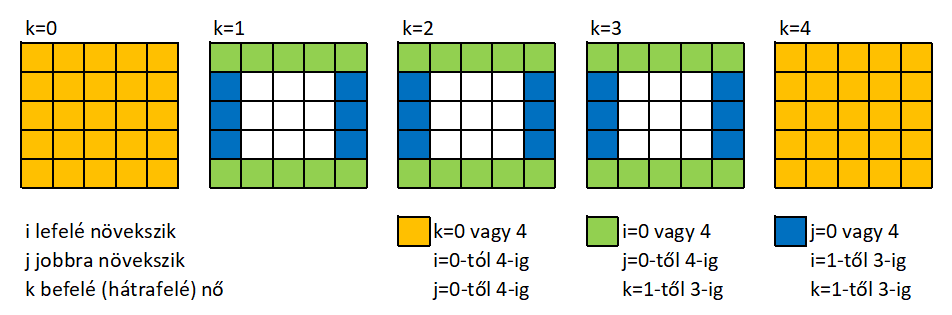
1. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
2. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
3. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
4. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
5. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
6. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 0 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
7. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 0 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
8. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 0 0 -3 | -3 0 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
9. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 0 0 -3 | -3 9 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
10. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 0 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
11. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 0 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
12. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 0 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
13. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 0 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
14. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
15. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 0 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
16. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 0 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
17. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 0 0 -3 | -3 2 17 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
18. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 0 -3 | -3 2 17 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
19. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 0 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
20. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
21. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
22. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 0 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
23. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 0 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
24. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 0 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
25. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 25 -3 | -3 8 11 0 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
26. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 25 -3 | -3 8 11 26 -3 | -3 9 10 0 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
27. lépés:
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 1 18 19 -3 | -3 2 17 20 -3 | -3 3 16 21 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 6 13 24 -3 | -3 5 14 23 -3 | -3 4 15 22 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -3 7 12 25 -3 | -3 8 11 26 -3 | -3 9 10 27 -3 | -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -2 -2 -2 -2 -2 | -1 -1 -1 -1 -1


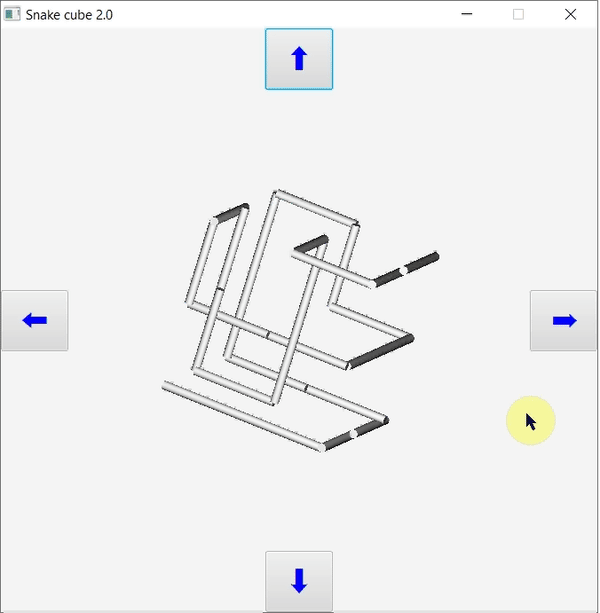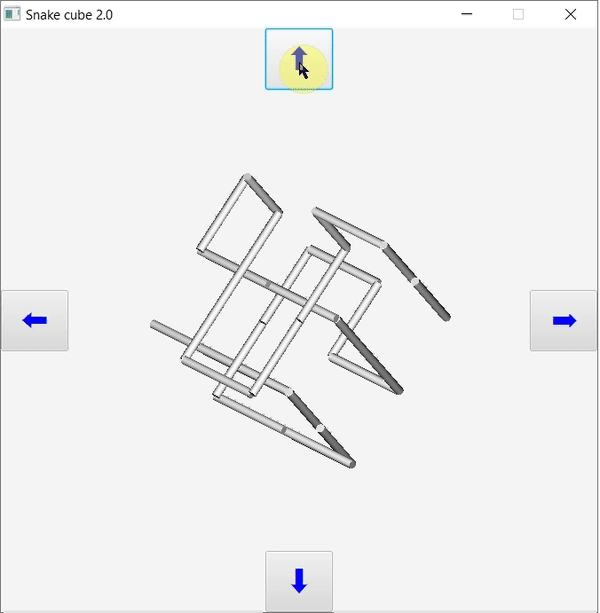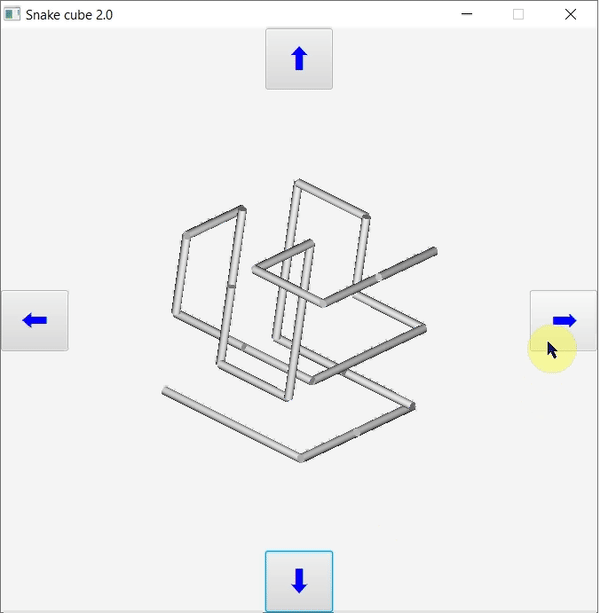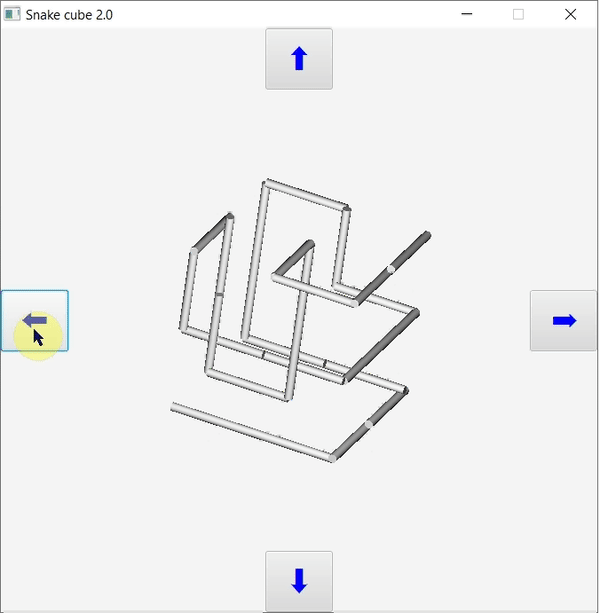
 A JavaFX grafikus felhasználói felületének és eseménykezelésének megvalósítása némileg eltér más Java GUI implementációk működésétől, például swing vagy Java3D. Főként animációk során hasznos használni. Megközelítése természetesen objektumorientált: a térbeli objektumok koordinátái, viselkedésük, transzformációkkal valósul meg, és azok is objektumok. A korábban elkészített konzolos kígyókocka programot valósítjuk meg most JavaFX GUI-val.
A JavaFX grafikus felhasználói felületének és eseménykezelésének megvalósítása némileg eltér más Java GUI implementációk működésétől, például swing vagy Java3D. Főként animációk során hasznos használni. Megközelítése természetesen objektumorientált: a térbeli objektumok koordinátái, viselkedésük, transzformációkkal valósul meg, és azok is objektumok. A korábban elkészített konzolos kígyókocka programot valósítjuk meg most JavaFX GUI-val.