Születésnap-paradoxon - it-tanfolyam.hu

Mennyi a valószínűsége, hogy n ember között van kettő, akiknek egy napon van a születésnapja? A meglepő a dologban az, hogy már 23 ember esetén a kérdéses valószínűség 1/2-nél nagyobb. Másképpen: már 23 ember esetén nagyobb annak az esélye, hogy megegyezik a születésnapjuk, mint az ellenkezőjének. Ez a 23 nagyon kevésnek tűnik. Ezért paradoxon.

Közismert néhány hétköznapi valószínűség. Íme néhány szabályos eset. A pénzfeldobás során 1/2 az esélye a fej és 1/2 az esélye az írás eredménynek (másképpen 50%-50%, azaz fifty-fifty). A kockadobás esetén 1/6 az esélye bármelyik számnak 1-től 6-ig. Két kocka esetén blogoltam már a dobott számok összegének alakulásáról, eloszlásáról: Kockadobás kliens-szerver alkalmazás.

Néhány egyszerűsítés

Az év 365 napból áll. Nem számítanak a 366 napos szökőévek.
A születések eloszlása egyenletes, azaz minden nap körülbelül ugyanannyian születnek. Nem számít, hogy hétköznap, hétvége, ünnepnap. Az áramszüneti városi legendák sem.
Nem vesszük figyelembe az azonos napon született ikreket. Persze ikrek születhetnek különböző napokon is.

Azonos születésnap valószínűsége grafikonon

Lássuk, hogyan alakul az azonos születésnap valószínűsége az emberek számától függően! Grafikonon ábrázolva:

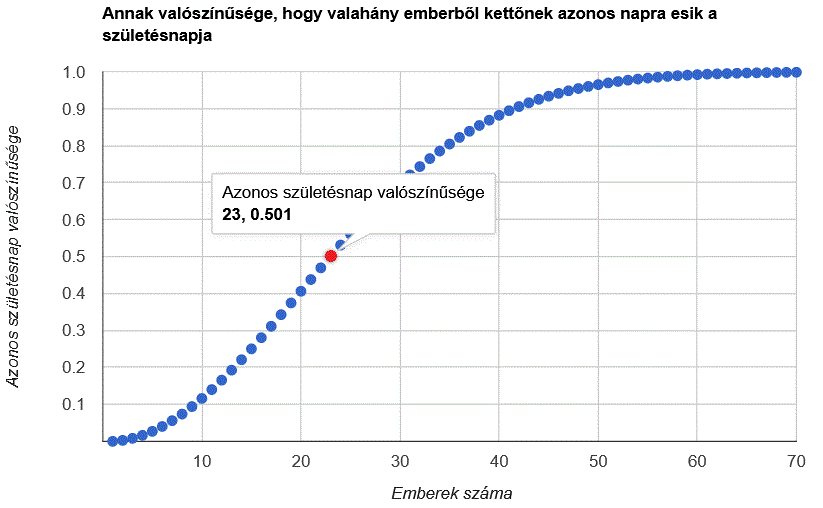
A fenti grafikonhoz szükséges adatok könnyen előállíthatók az alábbi Java forráskóddal:

private static String scatterChartData() {

List<String> list=IntStream.range(1, 71).boxed().

map(n->String.format(Locale.US,

"%10c[ %d, %.4f ]", ' ', n, 1-Math.pow(364.0/365, n*(n-1)/2))).

collect(Collectors.toList());

return String.join(",\n", list);

}

A fenti Google Chart típusú szórásgrafikon (Scatter Chart, korrelációs diagram) megjelenítéséhez adatpárok sorozata szükséges. Ezek a konkrétumok (70 db adatpár), görgethető:

[ 1, 0.0000 ],

[ 2, 0.0027 ],

[ 3, 0.0082 ],

[ 4, 0.0163 ],

[ 5, 0.0271 ],

[ 6, 0.0403 ],

[ 7, 0.0560 ],

[ 8, 0.0739 ],

[ 9, 0.0940 ],

[ 10, 0.1161 ],

[ 11, 0.1401 ],

[ 12, 0.1656 ],

[ 13, 0.1926 ],

[ 14, 0.2209 ],

[ 15, 0.2503 ],

[ 16, 0.2805 ],

[ 17, 0.3114 ],

[ 18, 0.3428 ],

[ 19, 0.3745 ],

[ 20, 0.4062 ],

[ 21, 0.4379 ],

[ 22, 0.4694 ],

[ 23, 0.5005 ],

[ 24, 0.5310 ],

[ 25, 0.5609 ],

[ 26, 0.5900 ],

[ 27, 0.6182 ],

[ 28, 0.6455 ],

[ 29, 0.6717 ],

[ 30, 0.6968 ],

[ 31, 0.7208 ],

[ 32, 0.7435 ],

[ 33, 0.7651 ],

[ 34, 0.7854 ],

[ 35, 0.8045 ],

[ 36, 0.8224 ],

[ 37, 0.8391 ],

[ 38, 0.8547 ],

[ 39, 0.8690 ],

[ 40, 0.8823 ],

[ 41, 0.8946 ],

[ 42, 0.9058 ],

[ 43, 0.9160 ],

[ 44, 0.9254 ],

[ 45, 0.9339 ],

[ 46, 0.9415 ],

[ 47, 0.9485 ],

[ 48, 0.9547 ],

[ 49, 0.9603 ],

[ 50, 0.9653 ],

[ 51, 0.9697 ],

[ 52, 0.9737 ],

[ 53, 0.9772 ],

[ 54, 0.9803 ],

[ 55, 0.9830 ],

[ 56, 0.9854 ],

[ 57, 0.9875 ],

[ 58, 0.9893 ],

[ 59, 0.9909 ],

[ 60, 0.9922 ],

[ 61, 0.9934 ],

[ 62, 0.9944 ],

[ 63, 0.9953 ],

[ 64, 0.9960 ],

[ 65, 0.9967 ],

[ 66, 0.9972 ],

[ 67, 0.9977 ],

[ 68, 0.9981 ],

[ 69, 0.9984 ],

[ 70, 0.9987 ]

Hasonló grafikon készítéséről szintén blogoltam már: Céline Dion – Courage World Tour.

Párok előállítása

Az emberek születésnapjainak összehasonlítása párokban történik. 23 ember esetén 23*22/2=253 pár van. Általános esetben n ember esetén (n*(n-1))/2 pár adódik. A levezetés részletei a források között megtalálható. 59 ember esetén 1711 pár adódik és szinte garantált az előforduló azonos születésnap, hiszen már 0,99 ennek a valószínűsége.

Az alábbi Java forráskód – rekurzív módon – előállítja a 23 konkrét esetre a párokat, az embereket 1-23-ig sorszámozva. Kombinációk:

private static void combinationsInternal(

List<Integer> input, int k,

List<List<Integer>> output,

ArrayList<Integer> acc, int i) {

int needToAcc=k-acc.size(), canAcc=input.size()-i;

if(acc.size()==k)

output.add(new ArrayList<>(acc));

else if(needToAcc<=canAcc) {

combinationsInternal(input, k, output, acc, i + 1);

acc.add(input.get(i));

combinationsInternal(input, k, output, acc, i + 1);

acc.remove(acc.size()-1);

}

public static List<List<Integer>> combinations(

List<Integer> input, int k) {

List<List<Integer>> output=new ArrayList<>();

combinationsInternal(input, k, output, new ArrayList<>(), 0);

return output;

}

public static void main(String[] args) {

for(int i=23; i<=23; i++) {

List<Integer> list=IntStream.range(1, i+1).

mapToObj(x->x).collect(Collectors.toList());

List<List<Integer>> combinationList=combinations(list, 2);

Collections.reverse(combinationList);

System.out.println(

i+" db elemből:\n"+

list+"\n"+

combinationList.size()+" db pár:\n"+

combinationList);

}

A main() metódusban az i változó paraméterezhető és a konkrét eset könnyen intervallumra változtatható. Eredményül ezt írja ki a program a konzolra, görgethető:

23 db elemből:

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]

253 db pár:

[[1, 2], [1, 3], [1, 4], [1, 5], [1, 6], [1, 7], [1, 8], [1, 9], [1, 10], [1, 11], [1, 12], [1, 13], [1, 14], [1, 15], [1, 16], [1, 17], [1, 18], [1, 19], [1, 20], [1, 21], [1, 22], [1, 23],

[2, 3], [2, 4], [2, 5], [2, 6], [2, 7], [2, 8], [2, 9], [2, 10], [2, 11], [2, 12], [2, 13], [2, 14], [2, 15], [2, 16], [2, 17], [2, 18], [2, 19], [2, 20], [2, 21], [2, 22], [2, 23],

[3, 4], [3, 5], [3, 6], [3, 7], [3, 8], [3, 9], [3, 10], [3, 11], [3, 12], [3, 13], [3, 14], [3, 15], [3, 16], [3, 17], [3, 18], [3, 19], [3, 20], [3, 21], [3, 22], [3, 23],

[4, 5], [4, 6], [4, 7], [4, 8], [4, 9], [4, 10], [4, 11], [4, 12], [4, 13], [4, 14], [4, 15], [4, 16], [4, 17], [4, 18], [4, 19], [4, 20], [4, 21], [4, 22], [4, 23],

[5, 6], [5, 7], [5, 8], [5, 9], [5, 10], [5, 11], [5, 12], [5, 13], [5, 14], [5, 15], [5, 16], [5, 17], [5, 18], [5, 19], [5, 20], [5, 21], [5, 22], [5, 23],

[6, 7], [6, 8], [6, 9], [6, 10], [6, 11], [6, 12], [6, 13], [6, 14], [6, 15], [6, 16], [6, 17], [6, 18], [6, 19], [6, 20], [6, 21], [6, 22], [6, 23],

[7, 8], [7, 9], [7, 10], [7, 11], [7, 12], [7, 13], [7, 14], [7, 15], [7, 16], [7, 17], [7, 18], [7, 19], [7, 20], [7, 21], [7, 22], [7, 23],

[8, 9], [8, 10], [8, 11], [8, 12], [8, 13], [8, 14], [8, 15], [8, 16], [8, 17], [8, 18], [8, 19], [8, 20], [8, 21], [8, 22], [8, 23],

[9, 10], [9, 11], [9, 12], [9, 13], [9, 14], [9, 15], [9, 16], [9, 17], [9, 18], [9, 19], [9, 20], [9, 21], [9, 22], [9, 23],

[10, 11], [10, 12], [10, 13], [10, 14], [10, 15], [10, 16], [10, 17], [10, 18], [10, 19], [10, 20], [10, 21], [10, 22], [10, 23],

[11, 12], [11, 13], [11, 14], [11, 15], [11, 16], [11, 17], [11, 18], [11, 19], [11, 20], [11, 21], [11, 22], [11, 23],

[12, 13], [12, 14], [12, 15], [12, 16], [12, 17], [12, 18], [12, 19], [12, 20], [12, 21], [12, 22], [12, 23],

[13, 14], [13, 15], [13, 16], [13, 17], [13, 18], [13, 19], [13, 20], [13, 21], [13, 22], [13, 23],

[14, 15], [14, 16], [14, 17], [14, 18], [14, 19], [14, 20], [14, 21], [14, 22], [14, 23],

[15, 16], [15, 17], [15, 18], [15, 19], [15, 20], [15, 21], [15, 22], [15, 23],

[16, 17], [16, 18], [16, 19], [16, 20], [16, 21], [16, 22], [16, 23],

[17, 18], [17, 19], [17, 20], [17, 21], [17, 22], [17, 23],

[18, 19], [18, 20], [18, 21], [18, 22], [18, 23],

[19, 20], [19, 21], [19, 22], [19, 23],

[20, 21], [20, 22], [20, 23],

[21, 22], [21, 23],

[22, 23]]

Kísérleti ellenőrzés

Tekintsünk például 1000 esetet! Készítsünk Java programot, amely 23 db véletlen születésnapot generál! Legyen ez a születésnap sorszáma az évben (másképpen hányadik napon született az ember az évben). Ez lényegesen egyszerűsíti a megoldást, összevetve a dátumkezelésen alapuló megközelítéssel. Ajánljuk a szakmai blog dátumkezelés címkéjét az érdeklődőknek, ahol megtalálhatók a témához kapcsolódó Java forráskódrészletek részletes magyarázatokkal kiegészítve. Íme a többféle generikus listát és programozási tételt használó forráskód:

public static void main(String[] args) {

final int COUNT=1000;

ArrayList<String> list1=new ArrayList<>();

int count2=0;

for(int i=1; i<=COUNT; i++) {

ArrayList<Integer> dayList=new ArrayList<>();

for(int n=1; n<=23; n++) {

int day=(int)(Math.random()*365+1); //1-365

dayList.add(day);

}

Collections.sort(dayList);

System.out.println(dayList);

ArrayList<String> list2=new ArrayList<>();

int n=0;

while(n<dayList.size()) {

int currentDay=dayList.get(n), count1=0;

while(n<dayList.size() && dayList.get(n)==currentDay) {

count1++;

n++;

}

if(count1>1)

list2.add(i+","+currentDay+","+count1);

}

if(!list2.isEmpty()) {

list1.add(list2.toString());

count2++;

}

System.out.println("\n"+list1+"\n"+COUNT+" esetből "+

count2+" kedvező eset fordult elő");

}

Érdemes elemezni, tesztelni a fenti forráskódot: milyen lépésekben, milyen adatszerkezeteket épít. Hasznos lehet lambda kifejezésekkel kiegészíteni, módosítani a programot. Részlet a program szöveges eredményéből:

[4, 14, 31, 34, 73, 85, 88, 110, 119, 125, 132, 140, 148, 183, 241, 249, 255, 265, 272, 289, 303, 353, 355]

[7, 16, 40, 67, 72, 72, 79, 89, 96, 128, 141, 142, 203, 215, 217, 219, 230, 243, 250, 272, 273, 321, 325]

[63, 70, 70, 87, 92, 106, 112, 113, 115, 123, 124, 131, 138, 139, 164, 165, 173, 177, 179, 180, 241, 310, 357]

[45, 48, 73, 75, 94, 103, 117, 161, 168, 170, 202, 223, 231, 235, 240, 252, 254, 255, 260, 272, 274, 284, 301]

[2, 2, 3, 13, 39, 47, 66, 94, 148, 151, 153, 160, 161, 166, 179, 212, 223, 254, 280, 311, 316, 324, 340]

[5, 32, 36, 71, 74, 80, 96, 115, 120, 150, 167, 167, 169, 219, 255, 259, 283, 289, 304, 306, 317, 336, 359]

[4, 5, 17, 46, 65, 78, 78, 79, 95, 106, 116, 138, 189, 228, 251, 253, 304, 332, 332, 334, 337, 347, 362]

[12, 14, 15, 67, 76, 77, 113, 126, 154, 161, 184, 195, 204, 214, 216, 225, 225, 225, 227, 229, 235, 236, 348]

[5, 7, 18, 28, 55, 71, 83, 126, 126, 129, 150, 158, 169, 221, 224, 231, 242, 253, 267, 300, 321, 326, 329]

[19, 37, 47, 49, 80, 89, 94, 122, 145, 165, 174, 190, 211, 215, 241, 265, 286, 287, 295, 297, 325, 354, 361]

...

[[2,72,2], [3,70,2], [5,2,2], [6,167,2], [7,78,2, 7,332,2], [8,225,3], [9,126,2]...

1000 esetből 506 kedvező eset fordult elő.

A 12. sorban lévő számhármasok jelentése: esetszám 1-től, azonos nap, előfordulás száma. Például: a kísérlet során a 8. esetben az év 225. napja azonos 3 embernél. Természetesen nincs garancia arra, hogy az 1000 eset vizsgálatánál mindig 500-nál nagyobb kedvező esetet kapunk.

A bejegyzéshez tartozó teljes forráskódot ILIAS e-learning tananyagban tesszük elérhetővé tanfolyamaink résztvevői számára.

A feladat a Java SE szoftverfejlesztő tanfolyam szakmai moduljának 17-28. óra Objektumorientált programozás alkalmaihoz kötődik.