Címke: JavaFX
3 blog bejegyzésnél szerepel:
44 db hozzá kapcsolódó címke:
2017 (24), 2022 (24), adatbázis (25), animáció (17), Applet (1), atipikus megoldás (5), ciklusok (18), élményalapú tanulás (21), fejtörő (11), funkcionális programozás (18), gamifikáció (33), grafika (26), grafikus felhasználói felület (40), játék (9), Java forráskód (63), JDBC (12), JSP (3), kígyókocka (2), konferencia (15), MMO (6), Multimédia az oktatásban konferencia (6), MVC (12), Neumann János Számítógép-tudományi Társaság (8), NJSZT Multimédia az oktatásban (6), NJSZT (8), objektumorientált programozás (85), orientáló modul (39), öröklődés (16), programozás (106), publikáció (9), rajzolás (15), rendezvény 2022 (8), Servlet (1), swing (26), szakmai előadás (31), szakmai modul (96), tananyagfejlesztés (8), tankocka (15), tervezés (41), többféle megoldás összehasonlítása (37), tömb (17), továbbfejlesztés (23), transzformáció (8), Unity (2)




 A
A 
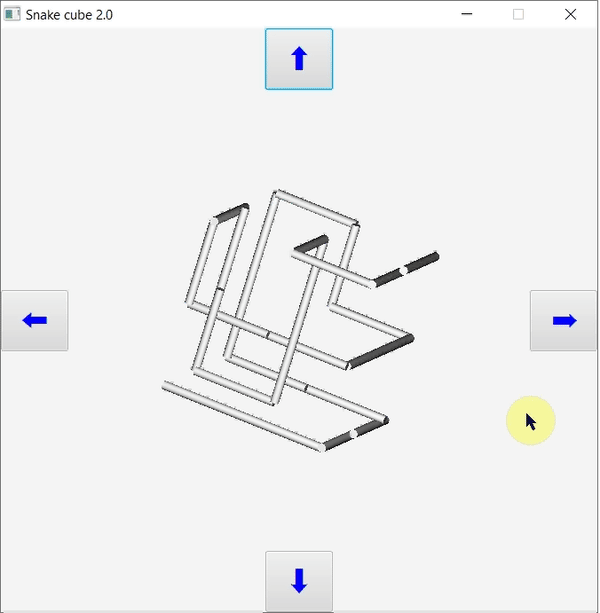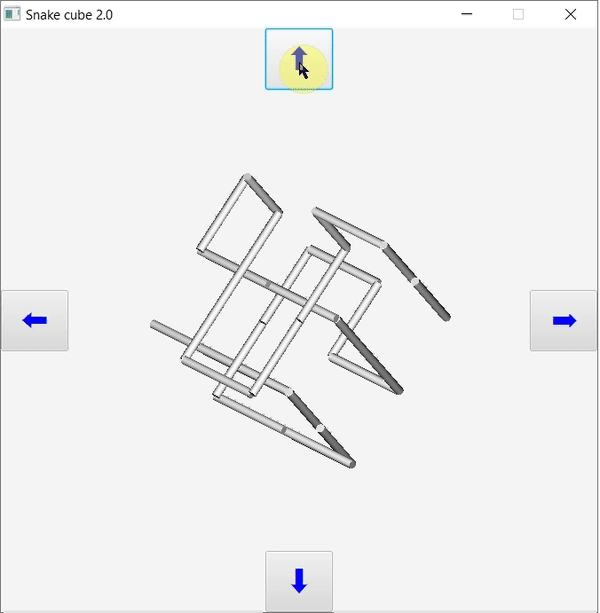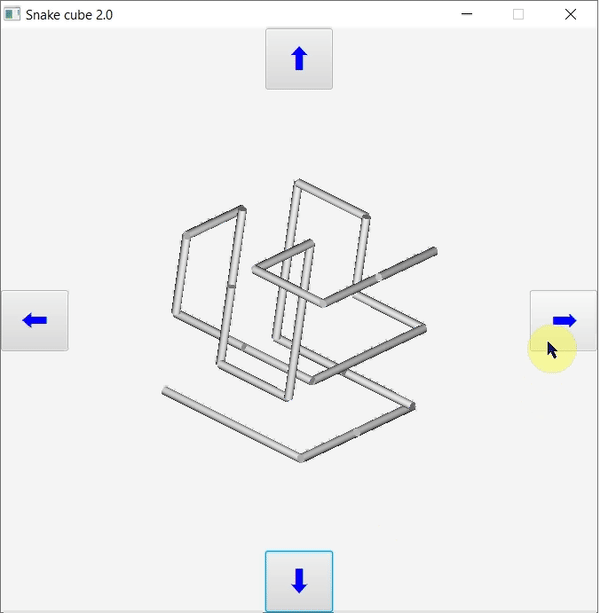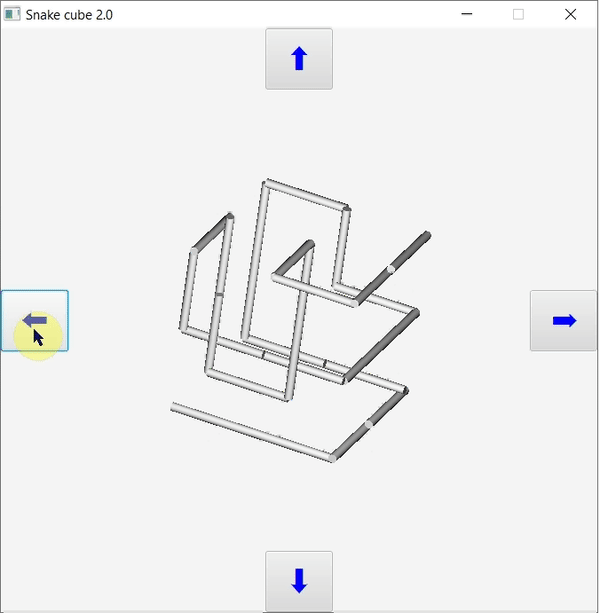
 A JavaFX grafikus felhasználói felületének és eseménykezelésének megvalósítása némileg eltér más Java GUI implementációk működésétől, például swing vagy Java3D. Főként animációk során hasznos használni. Megközelítése természetesen objektumorientált: a térbeli objektumok koordinátái, viselkedésük, transzformációkkal valósul meg, és azok is objektumok. A korábban elkészített konzolos kígyókocka programot valósítjuk meg most JavaFX GUI-val.
A JavaFX grafikus felhasználói felületének és eseménykezelésének megvalósítása némileg eltér más Java GUI implementációk működésétől, például swing vagy Java3D. Főként animációk során hasznos használni. Megközelítése természetesen objektumorientált: a térbeli objektumok koordinátái, viselkedésük, transzformációkkal valósul meg, és azok is objektumok. A korábban elkészített konzolos kígyókocka programot valósítjuk meg most JavaFX GUI-val.