Címke: lambda kifejezés
13 blog bejegyzésnél szerepel:
 Doktoranduszok programoznak – újratöltve
Doktoranduszok programoznak – újratöltve
 Kölcsönös ajándékozás véletlenszerűen
Kölcsönös ajándékozás véletlenszerűen
 Egy matematika érettségi feladat megoldása programozással 2023
Egy matematika érettségi feladat megoldása programozással 2023
 Egy matematika érettségi feladat megoldása programozással 2021
Egy matematika érettségi feladat megoldása programozással 2021
 Stream API lambda kifejezésekkel
Stream API lambda kifejezésekkel
72 db hozzá kapcsolódó címke:
2017 (24), 2018 (24), 2020 (24), 2021 (24), 2023 (24), 2024 (8), adatbázis (25), algoritmus (31), animáció (17), AnyChart (1), atipikus megoldás (5), becslés (6), ciklusok (18), címkefelhő (2), csoportváltás (6), dátumkezelés (10), doktori képzés (4), elosztott alkalmazás (14), érettségi feladat (8), euklideszi algoritmus (1), évforduló (24), fájlkezelés (29), fejtörő (11), funkcionális programozás (18), Google Charts (5), grafika (26), grafikus felhasználói felület (40), hatékonyság (28), hierarchikus lekérdezés (7), időzítő (4), Java forráskód (63), JavaScript (6), JDBC (12), JExcel API (4), kivételkezelés (13), kollekció (32), kombinatorika (7), könyvajánló (4), közelítés (3), leghosszabb közös részsorozat (1), legnagyobb közös osztó (1), lépésszám (9), logikai feladat (21), matematika érettségi feladat (8), matematika (30), memória használat (3), mesterséges intelligencia (12), metódus (30), naptár (26), objektumorientált programozás (85), orientáló modul (39), öröklődés (16), osztálydiagram (7), programozás (106), programozási tételek (28), rajzolás (15), rekurzió (9), statisztika (11), Stream API (14), swing (26), szakmai modul (96), szófelhő (2), tananyagfejlesztés (8), tervezés (41), tesztelés (21), többféle megoldás összehasonlítása (37), tömb (17), toplista (5), továbbfejlesztés (23), továbbképzés (4), ünnepnap (13), XML (8)

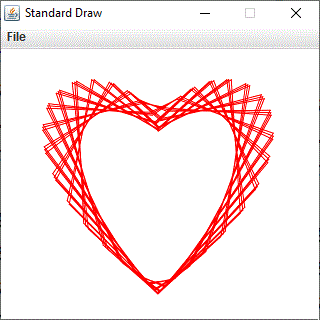





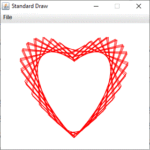 Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.
Szívgörbét ábrázolunk Java programmal. A Valentin-nap inspirálta ezt a feladatot. Számos matematikai görbe ismert, amelyek szívformához (kardioid) hasonlítanak. Szükséges egy megfelelő paraméteres görbe. A függvény szív formájú ábrája/grafikonja és egyenletrendszere alapján is nagy a választék.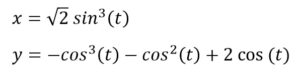

 Saját doktorandusz csoporttársaimmal én is többször beszélgettem már arról –
Saját doktorandusz csoporttársaimmal én is többször beszélgettem már arról –  A kölcsönös ajándékozás időről-időre több közösségben is felmerül. Munkahelyi környezetben és iskolai csoportokban is (például: Télapó, karácsony). Hagyományos megközelítésben így hangzik a szabály: „húzzunk neveket a kalapból”. Másképpen: mindenki 1 ajándékot ad, mindenki 1 ajándékot kap és a sorsolás véletlenszerűen történik.
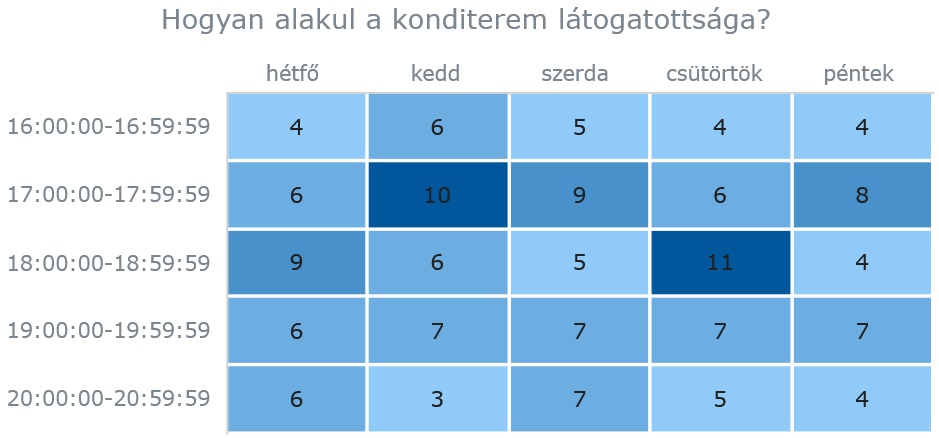
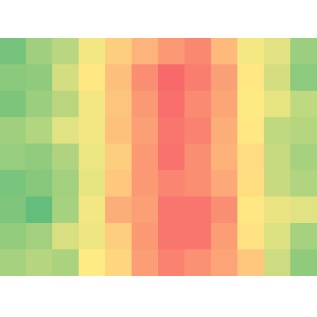
A kölcsönös ajándékozás időről-időre több közösségben is felmerül. Munkahelyi környezetben és iskolai csoportokban is (például: Télapó, karácsony). Hagyományos megközelítésben így hangzik a szabály: „húzzunk neveket a kalapból”. Másképpen: mindenki 1 ajándékot ad, mindenki 1 ajándékot kap és a sorsolás véletlenszerűen történik. Ebben a projektben táblázatos hőtérképet készítünk Java és JS nyelveken. Java programot készítünk az adatok véletlenszerű előállításához és a sablon alapján történő HTML fájl generálásához. JavaScript program fogja a grafikont megjeleníteni a weboldalon. Tervezünk, kódolunk, tesztelünk. Lássunk hozzá!
Ebben a projektben táblázatos hőtérképet készítünk Java és JS nyelveken. Java programot készítünk az adatok véletlenszerű előállításához és a sablon alapján történő HTML fájl generálásához. JavaScript program fogja a grafikont megjeleníteni a weboldalon. Tervezünk, kódolunk, tesztelünk. Lássunk hozzá!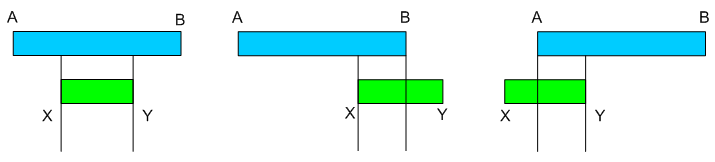
 A
A