Címke: metódus
30 blog bejegyzésnél szerepel:
 Dr. Sheldon Cooper kő-papír-olló-gyík-Spock játéka
Dr. Sheldon Cooper kő-papír-olló-gyík-Spock játéka
 Kép élesítése effektus működése
Kép élesítése effektus működése
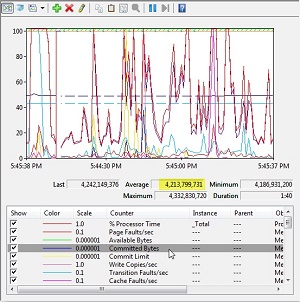 Java program memória használatának mérése
Java program memória használatának mérése
 Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
Beszámoló: it-tanfolyam.hu STEM nyári tábor 2023
 Egy matematika érettségi feladat megoldása programozással 2023
Egy matematika érettségi feladat megoldása programozással 2023
 Tankocka – Legyen Ön is milliomos! – Programozás Java nyelven
Tankocka – Legyen Ön is milliomos! – Programozás Java nyelven
 Tankocka – Egyszerű sorbarendezés: Java forráskód
Tankocka – Egyszerű sorbarendezés: Java forráskód
 Egy matematika érettségi feladat megoldása programozással 2022
Egy matematika érettségi feladat megoldása programozással 2022
 Egy matematika érettségi feladat megoldása programozással 2021
Egy matematika érettségi feladat megoldása programozással 2021
 Egy matematika érettségi feladat megoldása programozással 2020
Egy matematika érettségi feladat megoldása programozással 2020
 Egy matematika érettségi feladat megoldása programozással 2019
Egy matematika érettségi feladat megoldása programozással 2019
 Egy matematika érettségi feladat megoldása programozással 2018
Egy matematika érettségi feladat megoldása programozással 2018
 Egy matematika érettségi feladat megoldása programozással 2017
Egy matematika érettségi feladat megoldása programozással 2017
139 db hozzá kapcsolódó címke:
2017 (24), 2018 (24), 2019 (24), 2020 (24), 2021 (24), 2022 (24), 2023 (24), 2024 (8), adatbázis (25), Agymenők (3), algoritmus (31), alkalmazottak munkaköre (6), álláskeresés (17), animáció (17), ASCII (6), atipikus megoldás (5), becslés (6), brute force (7), ChatGPT (1), ciklusok (18), csoportmunka (10), csoportváltás (6), dátumkezelés (10), élményalapú tanulás (21), előadás műhely-napon (24), elosztott alkalmazás (14), érettségi feladat (8), euklideszi algoritmus (1), Euler (3), évforduló (24), fájlkezelés (29), fejtörő (11), felvételi feladat (4), Fibonacci (3), fizika (7), funkcionális programozás (18), gamifikáció (33), GitHub (2), Google Charts (5), Google Cloud Platform (2), grafika (26), grafikus felhasználói felület (40), hálózatkezelés (14), hatékonyság (28), humor (4), húsvétvasárnap (1), időzítő (4), IEEE Spectrum (2), Indeed (2), ipar 4.0 (6), ipar 5.0 (2), játék (9), Java forráskód (63), JFreeChart (7), karrier (17), karrierváltás (14), képeffektus (1), keresztrejtvény (2), kivételkezelés (13), kliens-szerver (7), kliensprogram (13), kockadobás (1), kollekció (32), kombinatorika (7), közelítés (3), kriptoaritmetika (2), lambda kifejezés (13), leghosszabb közös részsorozat (1), legnagyobb közös osztó (1), LEGO (3), lekérdezés (18), lépésszám (9), logikai feladat (21), logisztika (5), lottószelvény (10), matematika érettségi feladat (8), matematika (30), mém (7), memória használat (3), mesterséges intelligencia (12), munkaerőpiac (14), naptár (26), NASA (2), nyári tábor (2), okos gyár (5), objektumorientált programozás (85), OpenWeatherMap (2), optikai csalódás (2), orientáló modul (39), öröklődés (16), összefoglalás (2), pályaorientáció (28), pályázat (6), PDF (1), péntek 13 (1), Pi nap (2), Pi (2), ProgCont API (3), programozás (106), programozási tételek (28), projektmunka (5), PYPL (2), Python (4), rajzolás (15), Reddit (2), rekurzió (9), rendezvény 2023 (10), robotika (12), robotprogramozás (11), soft skill (10), Stack Overflow (2), statisztika (11), STEM (3), Stream API (14), swing (26), szakmai előadás (31), szakmai modul (96), szimuláció (10), sztereogram (1), tananyagfejlesztés (8), tankocka (15), tervezés (41), tesztelés (21), tévésorozat (3), TIOBE (2), tipikus munkanap (6), többféle megoldás összehasonlítása (37), tömb (17), tömegvonzás (5), továbbfejlesztés (23), transzformáció (8), Trendy Skills (2), UML (8), ünnepnap (13), vélemény (4), videó (5), virtuális valóság (5), visszajelzés (5), XML (8)














 Azokat a számpárokat, amelyekre igaz, hogy az egyik szám önmagánál kisebb osztóinak összege megegyezik a másik számmal és fordítva, külön-külön barátságos számoknak, együtt barátságos számpárnak hívjuk.
Azokat a számpárokat, amelyekre igaz, hogy az egyik szám önmagánál kisebb osztóinak összege megegyezik a másik számmal és fordítva, külön-külön barátságos számoknak, együtt barátságos számpárnak hívjuk. A 2018-as középszintű matematika érettségi feladatsor 10. feladata inspirált arra, hogy a programozás eszköztárával oldjuk meg ezt a feladatot. Szükséges hozzá néhány programozási tétel: sorozatszámítás, eldöntés, kiválasztás. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az
A 2018-as középszintű matematika érettségi feladatsor 10. feladata inspirált arra, hogy a programozás eszköztárával oldjuk meg ezt a feladatot. Szükséges hozzá néhány programozási tétel: sorozatszámítás, eldöntés, kiválasztás. Érdekes belegondolni, hogy mennyire más lehetne a problémamegoldás, ha programozhatnánk a matematika érettségi vizsgán. A teljes feladatsor a megoldásokkal együtt letölthető az  A
A 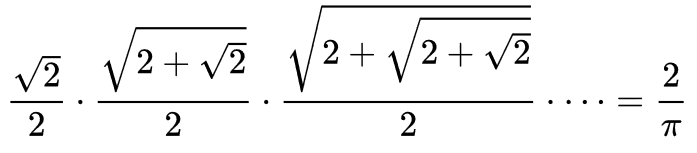
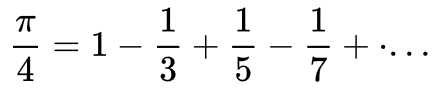
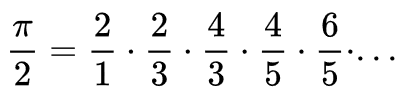
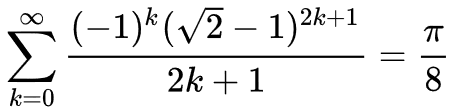



 A
A